The product of two complex numbers is similar to the product of two real numbers, namely: the product is considered as a number made up of a multiplicand, just as a factor is made up of one. The vector corresponding to a complex number with modulus r and argument j can be obtained from a unit vector whose length is one and whose direction coincides with the positive direction of the OX axis by lengthening it r times and rotating it in the positive direction by an angle j. The product of some vector a 1 and vector a 2 is the vector that will be obtained if we apply lengthening and rotation to the vector a 1, with the help of which the vector a 2 is obtained from a unit vector, and the latter obviously corresponds to a real unit. If (r 1 , ? 1), (r 2 , ? 2) are modules and arguments of complex numbers corresponding to vectors a 1 and a 2 , then the product of these vectors will obviously correspond to a complex number with module r 1 r 2 and argument (j1 + j2). Thus, the product of two complex numbers is such a complex number, the modulus of which is equal to the product of the modules of the factors and the argument is the sum of the arguments of the factors.

In the case when complex numbers are written in trigonometric form, we will have

r 1 (cos? 1 + i sin? 1) * r 2 (cos? 2 + i sin? 2) = r 1 r 2.

In the case (a 1 + b 1 i) (a 2 + b 2 i) = x + yi, using the notation of modules and arguments of factors, we can write:

a 1 = r 1 cos? 1 ; b 1 \u003d r 1 sin? 1 ; a 2 = r 2 cos? 2; b 2 \u003d r 2 sin? 2;

according to the definition of multiplication:

x = r 1 r 2 cos(? 1 + ? 2); y = r 1 r 2 sin(? 1 + ? 2),

x = r 1 r 2 (cos? 1 cos? 2 - sin? 1 sin? 2) = = r 1 cos? 1 r 2 cos? 2 - r 1 sin? 1 r 2 sin? 2 = a 1 a 2 - b 1 b 2

y = r 1 r 2 (sin? 1 cos? 2 + cos? 1 sin? 2) = = r 1 sin? 1 r 2 cos? 2 + r1 cos? 1 r 2 sin? 2 \u003d b 1 a 2 + a 1 b 2,

and finally we get:

(a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2) i.

In the case b 1 = b 2 = 0, the factors are real numbers a 1 and a 2 and the product is reduced to the product a 1 a 2 of these numbers. When

a 1 = a 2 = 0 and b 1 = b 2 = 1,

the equality (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I gives: i???i = i 2 = -1, i.e. the square of the imaginary unit is -1. Calculating sequentially positive integer powers of i, we get:

i 2 \u003d -1; i 3 \u003d -i; i4 = 1; i 5 = i; i 6 = -1; ...

and, in general, for any positive k:

i 4k = 1; i 4k+1 = i; i 4k+2 = -1; i 4k+3 = -i

The multiplication rule expressed by the equality (a 1 + b 1 i) (a 2 + b 2 i) \u003d (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2) I can be formulated as follows: complex numbers must be multiplied like literal polynomials, counting i 2 = -1.

From the above formulas it directly follows that the addition and multiplication of complex numbers obey the commutative law, i.e. the sum does not depend on the order of the terms, and the product does not depend on the order of the factors. It is not difficult to check the validity of the associative and distributive laws expressed by the following identities:

(? 1 + ? 2) + ? 3 = ? 1 + (? 2 + ? 3); (? 1 ? 2)? 3 = ? 1 (? 2 ? 3); (? 1 + ? 2)? = ? 1 ? + ? 2 ? .

The product of several factors will have a modulus equal to the product of the modules of the factors, and an argument equal to the sum of the arguments of the factors. Thus, the product of complex numbers will be equal to zero if and only if at least one of the factors is equal to zero.

Example: given complex numbers z 1 = 2 + 3i, z 2 = 5 - 7i. Find:

a) z 1 + z 2; b) z 1 - z 2; c) z 1 z 2 .

a) z 1 + z 2 \u003d (2 + 3i) + (5 - 7i) \u003d 2 + 3i + 5 - 7i \u003d (2 + 5) + (3i - 7i) \u003d 7 - 4i; b) z 1 - z 2 \u003d (2 + 3i) - (5 - 7i) \u003d 2 + 3i - 5 + 7i \u003d (2 - 5) + (3i + 7i) \u003d - 3 + 10i; c) z 1 z 2 \u003d (2 + 3i) (5 - 7i) \u003d 10 - 17i + 15i - 21i 2 \u003d 10 - 14i + 15i + 21 \u003d (10 + 21) + (- 14i + 15i) \u003d 31 + i (here it is taken into account that i 2 = - 1).

Example: do the following:

a) (2 + 3i) 2 ; b) (3 - 5i) 2 ; c) (5 + 3i) 3 .

a) (2 + 3i) 2 = 4 + 2×2×3i + 9i 2 = 4 + 12i - 9 = - 5 + 12i; b) (3 - 5i) 2 \u003d 9 - 2H3H5i + 25i 2 \u003d 9 - 30i - 25 \u003d - 16 - 30i; c) (5 + 3i) 3 \u003d 125 + 3×25×3i + 3×5×9i 2 + 27i 3; since i 2 \u003d - 1, and i 3 \u003d - i, then we get (5 + 3i) 3 \u003d 125 + 225i - 135 - - 27i \u003d - 10 + 198i.

Example: perform actions

a) (5 + 3i)(5 - 3i); b) (2 + 5i)(2 - 5i); c) (1 + i)(1 - i).

a) (5 + 3i)(5 - 3i) = 5 2 - (3i) 2 = 25 - 9i 2 = 25 + 9 = 34; b) (2 + 5i)(2 - 5i) = 2 2 - (5i) 2 = 4 + 25 = 29; c) (1 + i)(1 - i) = 1 2 - i 2 = 1 + 1 = 2.

A complex number is a number of the form , where and are real numbers, the so-called imaginary unit. The number is called real part () complex number, the number is called imaginary part () complex number.

Complex numbers are displayed on complex plane:

As mentioned above, it is customary to denote the set of real numbers by a letter. A bunch of same complex numbers it is customary to designate it as a "bold" or thickened letter. Therefore, the letter should be put on the drawing, denoting the fact that we have a complex plane.

Algebraic form of a complex number. Addition, subtraction, multiplication and division of complex numbers

Addition of complex numbers

To add two complex numbers, add their real and imaginary parts:

z 1 + z 2 = (a 1 + a 2) + i*(b 1 + b 2).

For complex numbers, the rule of the first class is valid: z 1 + z 2 \u003d z 2 + z 1 - the sum does not change from the rearrangement of the terms.

Subtraction of complex numbers

The action is similar to addition, the only feature is that the subtrahend must be taken in brackets, and then, as a standard, open these brackets with a sign change:

z 1 + z 2 \u003d (a 1 - a 2) + i * (b 1 - b 2)

Multiplication of complex numbers

Basic equality of complex numbers:

Product of complex numbers:

z 1 * z 2 = (a 1 + i*b 1)*(a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b 1 *b 2 = a 1 *a 2 - b 1 *b 2 +i*(a 1 *b 2 +a 2 *b 1).

Like the sum, the product of complex numbers is permutable, that is, the equality is true: .

Division of complex numbers

The division of numbers is carried out by multiplying the denominator and numerator by the conjugate expression of the denominator.

2 Question. complex plane. Modulus and arguments of complex numbers

Each complex number z = a + i*b can be associated with a point with coordinates (a;b) , and vice versa, each point with coordinates (c;d) can be associated with a complex number w = c + i*d . Thus, a one-to-one correspondence is established between the points of the plane and the set of complex numbers. Therefore, complex numbers can be represented as points in a plane. The plane on which complex numbers are drawn is usually called complex plane.

However, more often complex numbers are depicted as a vector with origin at the point O, namely, the complex number z \u003d a + i * b is represented by the radius vector of the point with coordinates (a; b). In this case, the image of complex numbers from the previous example will be like this:

The image of the sum of two complex numbers , is a vector equal to the sum of the vectors representing the numbers and . In other words, when adding complex numbers, the vectors representing them are also added.

Let the complex number z = a + i*b be represented by a radius vector. Then the length of this vector is called module number z and is denoted by |z| .

The angle formed by the radius vector of a number with the axis is called argument numbers and is denoted by arg z . The number argument is not defined uniquely, but up to a multiple of . However, usually the argument is given in the range 0 or in the range -to. In addition, the number argument is not defined.

Using this relation, you can find the argument of a complex number:

moreover, the first formula is valid if the image of the number is in the first or fourth quarter, and the second, if it is in the second or third. If , then the complex number is represented by a vector on the Oy axis and its argument is /2 or 3*/2.

Let's get one more useful formula. Let z = a + i*b . Then ,

Complex numbers- this is the minimum extension of the set of real numbers familiar to us. Their fundamental difference is that an element appears that squared gives -1, i.e. i, or .

Any complex number has two parts: real and imaginary:

Thus, it is clear that the set of real numbers coincides with the set of complex numbers with zero imaginary part.

The most popular model for the set of complex numbers is the ordinary plane. The first coordinate of each point will be its real part, and the second - imaginary. Then the role of the complex numbers themselves will be vectors with the beginning at the point (0,0).

Operations on complex numbers.

In fact, if we take into account the model of the set of complex numbers, it is intuitively clear that addition (subtraction) and multiplication of two complex numbers are performed in the same way as the corresponding operations on vectors. And it means vector product vectors, because the result of this operation is again a vector.

1.1 Addition.

(As you can see, this operation exactly corresponds to )

1.2 Subtraction, similarly, is performed according to the following rule:

2. Multiplication.

3. Division.

It is defined simply as the inverse operation of multiplication.

trigonometric form.

The modulus of a complex number z is the following quantity:

,

it is obvious that this, again, is simply the modulus (length) of the vector (a,b).

Most often, the modulus of a complex number is denoted as ρ.

It turns out that

z = ρ(cosφ+isinφ).

The following follows directly from the trigonometric form of writing a complex number. formulas :

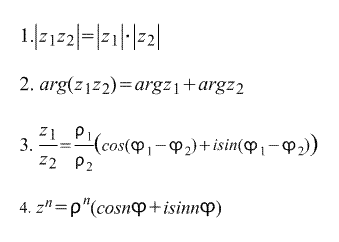
The last formula is called De Moivre formula. The formula is derived directly from it. nth root of a complex number:

thus, there are n nth roots of the complex number z.

While addition and subtraction of complex numbers is more convenient to do in algebraic form, multiplication and division is easier to do using the trigonometric form of complex numbers.

Take two arbitrary complex numbers given in trigonometric form:

Multiplying these numbers, we get:

But according to the formulas of trigonometry

Thus, when complex numbers are multiplied, their moduli are multiplied, and the arguments

add up. Since in this case the modules are converted separately, and the arguments - separately, performing multiplication in trigonometric form is easier than in algebraic.

Equation (1) implies the relations:

Since division is the inverse of multiplication, we get that

In other words, the module of the quotient is equal to the ratio modules of the dividend and the divisor, and the argument of the quotient is the difference between the arguments of the dividend and the divisor.

Let us now dwell on the geometric meaning of multiplication of complex numbers. Formulas (1) - (3) show that to find the product, you must first increase the modulus of the number of times without changing its argument, and then increase the argument of the resulting number by without changing its modulus. The first of these operations geometrically means a homothety with respect to the point O with a coefficient , and the second - a rotation relative to the point O by an angle equal to Considering here one factor is constant and the other is variable, we can formulate the result as follows: formula

We define the product of two complex numbers in the same way as the product of real numbers, namely: the product is considered as a number made up of a multiplicand, just as a factor is made up of unity.

The vector corresponding to a complex number with modulus and argument can be obtained from a unit vector whose length is equal to one and whose direction coincides with the positive direction of the OX axis, by lengthening it by a factor and turning it in the positive direction by an angle

By the product of a certain vector by a vector we mean the vector that will be obtained if the above extension and rotation are applied to the vector, with the help of which the vector is obtained from a unit vector, and the latter obviously corresponds to a real unit.

If the essence is modules and arguments of complex numbers corresponding to vectors, then the product of these vectors will obviously correspond to a complex number with module and argument . We thus arrive at the following definition of the product of complex numbers:

The product of two complex numbers is such a complex number, the modulus of which is equal to the product of the modules of the factors and the argument is the sum of the arguments of the factors.

Thus, in the case when complex numbers are written in trigonometric form, we will have

We now derive the rule for compiling a product for the case when complex numbers are not given in trigonometric form:

Using the above notation for modules and arguments of factors, we can write

according to the definition of multiplication (6):

and finally we get

In the case, the factors are real numbers and the product is reduced to the product ahag of these numbers. In the case, equality (7) gives

i.e. the square of the imaginary unit is

Calculating consecutively positive integer powers , we obtain

and in general, for every positive integer

The multiplication rule expressed by equality (7) can be formulated as follows: complex numbers must be multiplied as literal polynomials, considering

If a is a complex number, then the complex number is called the conjugate of a, and it is denoted by a. According to formulas (3), we have from equality (7) it follows

and consequently,

i.e., the product of conjugate complex numbers is equal to the square of the modulus of each of them.

Let us also note the obvious formulas

From formulas (4) and (7) it directly follows that the addition and multiplication of complex numbers obey the commutative law, i.e. the sum does not depend on the order of the terms, and the product does not depend on the order of the factors. It is not difficult to check the validity of the associative and distributive laws expressed by the following identities:

We leave this to the reader.

Finally, note that the product of several factors will have a modulus equal to the product of the modules of the factors, and an argument equal to the sum of the arguments of the factors. Thus, the product of complex numbers will be equal to zero if and only if at least one of the factors is equal to zero.