Download from Depositfiles

DIFFERENTIAL GEOMETRY

I. VECTOR FUNCTION OF SCALAR ARGUMENT

Vector function (definition 1.1), methods for specifying it.

Radius vector and hodograph, parametric hodograph specification.

Derivative of a vector function (Definition 1.6).

Geometric meaning of the derivative of a vector function.

Rules for differentiation of vector functions.

1.1. DEFINITION OF VECTOR FUNCTION

Definition 1.1If each value of the scalar argumentmatched vector
three-dimensional space R 3 , then they say that a vector function (or vector function) of a scalar argument is given on the set Xt .

If in space R 3 a Cartesian coordinate system is specifiedABOUT xyz , then the task is a vector - function
,
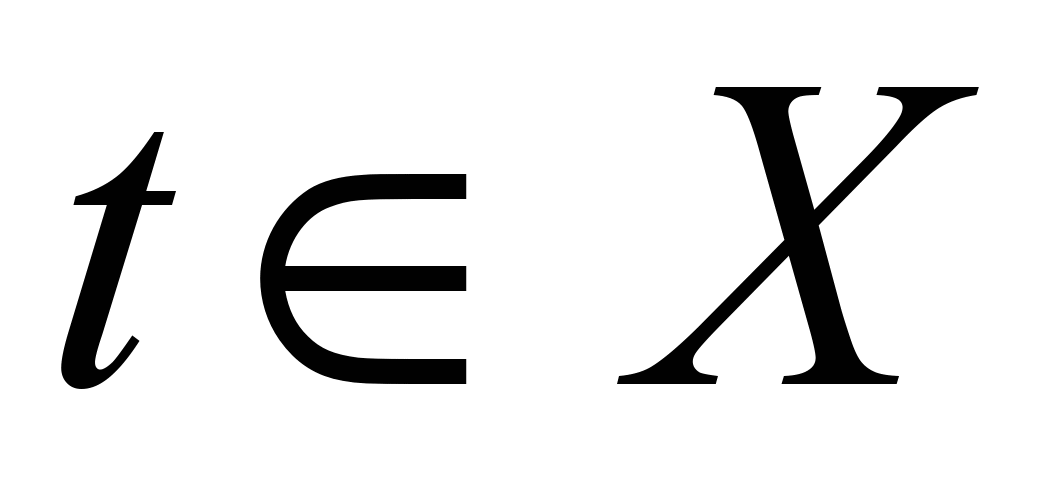is equivalent to specifying three scalar functionsX( t ), y ( t ), z ( t ) – vector coordinates:

= { x ( t ), y ( t ), z ( t )} (1.1)

or , (1.2)

Where
— coordinate unit vectors.

1.2. SPATIAL LINE AS A HODOGRAPH OF RADIUS VECTOR

Definition 1.2 If the beginning of all vectors is ,placed at the origin, they are called radius vectors.

Definition 1.3 The line that is the geometric locus of the ends of the radius vectors , , is called the hodograph of the vector function, and their common beginning is the hodograph pole.

If the parameter t is time, and is the radius vector of the moving point, then the hodograph of the function is the trajectory of the moving point.

The hodograph equation can be written in vector form (1.2) or in parametric form:

(1.3)

In particular, if the vector functionwith a change in the argument, only its module changes, but the direction does not change (), then the hodograph of such a vector function will be a rectilinear ray emanating from the origin; if only the direction of the vector changes, but its magnitude remains unchanged (
), then the hodograph of the vector function will be a curve located on a sphere with a center at the pole and a radius equal to the constant modulus of the vector.

Picture 1.

1.3. LIMIT, CONTINUITY AND DERIVATIVE OF VECTOR–FUNCTION

Definition 1. 4 Vector is called the limit of the vector functionat
, If

. (1.4)

Definition 1.5 The vector function is called continuous at a pointt 0, if it has a limit at this point equal to the value of the vector function at this point:

. (1.5)

Definition 1.6Derivative of a vector function at the point t is called the limit of the ratio of the increment of a vector function to the increment of the argument
at
:

(1.6)

1.4. GEOMETRICAL AND MECHANICAL MEANING OF THE FIRST DERIVATIVE OF THE VECTOR FUNCTION

The geometric meaning of the first derivative of the vector function of the scalar argument is that this derivative is a new vector directed tangentially to the hodograph:
. Let's show it.

Figure 2

We will assume that the hodograph of the vector function under consideration is a continuous line that has a tangent at any point.

Let's give the argument t increment, then geometrically the ratio
is some vector
, lying on the secant MM’. When this vector rotates and turns into a vector
, lying on the tangent and directed towards increasingt . So the vector

(1.7)

will be a unit tangent vector oriented in the direction of increasing parametert .

Therefore, the vector
can be taken as a direction vector tangent to the curve at point ), (or
), and write the tangent equation in the form:

(1.8)

If t – time, and — radius vector of a point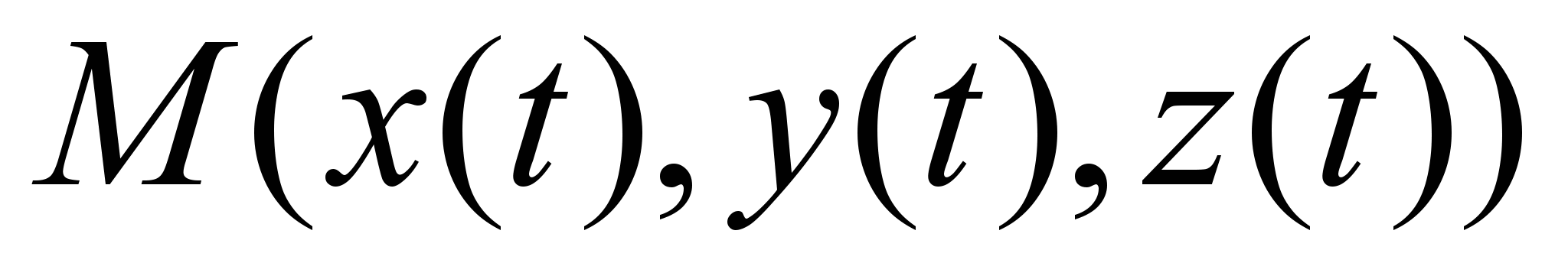
, moving in three-dimensional space, then aboutthe relationship is called the average speed of a point on the segment [t; t+t].

Mechanical sensethe first derivative of the vector function is that this derivative represents the speed of point M at the momentt :

Rules for differentiation of vector functions

Let's prove rule 1 using the rules for subtracting vectors and dividing a vector by a number:

The proof of the remaining rules is based on rule 1 and the rules for operating with vectors.

Example 1.1: Given a vector function.Construct its hodograph and create an equation for its tangent at an arbitrary point.

Solution. For any point ( x , y , z ) hodograph vector – functions we have:x = acost ; y = asint ; z = bt and therefore for any
equality holdsx 2 + y 2 = a 2 , and the generatrix is ​​parallel to the axis Oz. If the parameter t interpreted as time, then with uniform motion around a circle the projection of the end of the radius vector onto the planeOxy its projection onto the axisOz will move uniformly and rectilinearly at speedb . In other words, the applicate of a hodograph point of a vector function grows in proportion to the angle of rotation of its projection onto the planeOxy . Therefore, the desired hodograph will have the form shown in Fig. 3 and it is called a helical line. To find the tangents to the hodograph (helical line), we find the derivative of the vector function.

Solution. Because the, then

and its differentiation.

One of the simplest ways to specify a spatial curve is to specify a vector equation:

Where is the radius vector of the curve point, and - parameter that determines the position of the point.

That. variable vector there is a scalar function . In mathematical analysis, such functions are called vector functions of a scalar argument.

Decomposing using unit vectors, equation (1) can be given the form:

This expansion makes it possible to move on to the parametric equation of the curve:

In other words, specifying a vector function is equivalent to specifying three scalar ones.

In relation to the vector function (1) that defines this curve, the curve itself is called the hodograph of this function. The origin of coordinates is called in this case the pole of the hodograph.

Let it now
And
- points of the curve defined by equation (1). Moreover
, A
The radius vectors of these points will be

And
.

Vector
called the increment of a vector function
, corresponding to the increment
its argument, and is denoted by
,

Vector function
will be a continuous function , If

.

To find the derivative of
let's proceed as follows -

.

Let's now set the direction
. It's obvious that collinear with
and at
directed in the same direction as
and when
- in the opposite direction. But in the first case
and in the second
That. vector always directed along the secant hodograph
upward .

If we use the expansion And by orts, then

From here dividing (*) by
and going to the limit
For
we get

Based on (4), it can be shown that the following formulas are valid:

(5)

(6)

- scalar function.

Proof (7).

Let us now examine some properties
. First of all, let's find its module:

.

Because we consider the hodograph arc to be rectifiable, then
- is the length of the chord, and
- arc length. That's why

That. the modulus of the derivative of the vector function of a scalar argument is equal to the derivative of the hodograph arc with respect to the same argument.

Corollary 1. If - unit vector directed tangentially to the hodograph in the direction of increase , That

Corollary 2. If the length of the hodograph arc is taken as the argument of the vector function , That

(because
)

That. the derivative of the vector function along the length of the arc of the hodograph is equal to the unit vector of the tangent to the hodograph, directed towards increasing the length of the arc.

Corollary 3. If the hodograph of a vector function is considered as the trajectory of a point, and - as the time of movement, counted from a certain , That
coincides in magnitude and direction with the motion velocity vector
.

In fact, the scalar value of speed is equal to the derivative of the path with respect to time:

In addition, the vector directed tangentially to the trajectory in the direction of movement, which corresponds to the direction of increase , i.e. corresponds to the direction .

That.
.

Let's now consider
, whose length is constant,
, i.e.

(*)
Where

Differentiating (*), we find:

Those.

In particular, the derivative of a vector of any variable in the direction of unit Always
.

Let it now
the angle between the radii of the unit sphere drawn to the points
And
hodograph
. Then the chord length
from a triangle
will be equal

The magnitude of the derivative of a unit variable vector is equal to the angular velocity of rotation of this vector.

As for scalar functions, the differential of a vector function is written as

But even then

Curvature of a spatial curve.

Accompanying trihedron.

According to Corollary 2, for we can write the formula:

Changing direction , associated with a change in the tangent to the spatial curve, characterizes the curvature of the curve. As a measure of the curvature of a spatial curve, as for a plane curve, the limit of the ratio of the angle of adjacency to the length of the arc is taken, when

curvature,
angle of adjacency,
arc length.

On the other side,
unit vector and its derivative vector is perpendicular to it, and its modulus
Differentiating By and entering
unit vector with direction , we find:

Vector
curvature vector of a space curve. Its direction, perpendicular to the tangent direction, is the normal direction of the space curve. But a spatial curve has at any point an infinite number of normals, which all lie in a plane passing through a given point of the curve and perpendicular to the tangent at a given point. This plane is called the normal plane of the spatial curve.

Definition. The normal of the curve along which the curvature vector of the curve is directed at a given point is the main normal of the spatial curve. That.
unit principal normal vector.

Let us now construct the third unit vector equal to the cross product And

Vector , as well as also perpendicular those. lies in the normal plane. Its direction is called the direction of the binormal of the spatial curve at a given point. Vector
And constitute a trio of mutually perpendicular unit vectors, the direction of which depends on the position of the point on the spatial curve and varies from point to point. These vectors form the so-called. accompanying trihedron (Frenet trihedron) of a spatial curve. Vector
And form a right triple, just like the unit unit vectors
in the right coordinate system.

Taken in pairs
define three planes passing through the same point on the curve and forming the faces of the accompanying trihedron. Wherein And determine the osculating plane (the arc of a curve in the vicinity of a given point is the arc of a plane curve in the osculating plane to an accuracy of higher order);

And - straightening plane;

And - normal plane.

Tangent, normal and binormal equations.

Equations of the planes of the accompanying trihedron.

Knowing
And , or any non-unit vectors collinear to them T, N And B Let us derive the equations named in this section.

To do this, in the canonical equation of the straight line

and in the equation of the plane passing through a given point

take for
coordinates of the point selected on the curve, for
or respectively for
take the coordinates of that of the vectors
or
, which determines the direction of the desired line or normal to the desired plane:

or - for a tangent or normal plane,

or - for the main normal and straightening plane,

or - for binormal and osculating plane.

If the curve is given by the vector equation
or
then for the vector
directed tangentially can be taken

To find
And let's first find the decomposition
by vectors
Previously (Corollary 1) we found that
Differentiating by , we get:

But, because

Let us now multiply vectorially And

(*)

Based on (*) per vector , having a binormal direction, we could take the vector

But then, for
we can take the vector product of these latter:

That. at any point on an arbitrary curve we can determine all the elements of the accompanying trihedron.

Example. Equation of tangent, normal and binormal to the right helix at any point.

Tangent

Home normal

Binormal

Let the set of values ​​of the vector function of the scalar argument be reduced to a common origin at point 0. Let us match the origin of the Cartesian coordinate system with this point. Then for any vector can be expanded into unit vectors

Thus, specifying a vector function of a scalar argument means specifying three scalar functions When the value of the argument changes, the end of the vector will describe a curve in space, which is called the vector hodograph

Let there be a close value for Then the derivative of a vector function to a scalar argument is called

No. 17 Speed ​​and acceleration of a point in curvilinear motion

Speed

Velocity is introduced as a characteristic of the movement of a material point. Speed ​​is a vector quantity, which is characterized by both the speed of movement (velocity vector magnitude) and its direction (velocity vector direction) at a given time. Let a material point move along some curvilinear trajectory, and at the moment of time t it corresponds to the radius vector r0 (Fig. 1). In a short period of time Δt, the point will travel Δs and at the same time receive an elementary (infinitesimal) displacement Δr.

Average speed vector is called the ratio of the increment Δr of the radius vector of a point to the time interval Δt:

The direction of the average velocity vector coincides with the direction of Δr. With an infinite decrease in Δt, the average speed tends to a value called instantaneous speed v:

This means that the instantaneous speed v is a vector quantity, which is equal to the first derivative of the radius vector of the moving point with respect to time. Because in the limit, the secant coincides with the tangent, then the velocity vector v is directed tangent to the trajectory in the direction of movement (Fig. 2).

Fig.2

As Δt decreases, Δs will increasingly approach |Δr|, so the instantaneous velocity module

This means that the absolute value of the instantaneous speed is equal to the first derivative of the path with respect to time:

With uneven motion, the instantaneous velocity module is different at different times. In this case, use the scalar quantity - average speed of uneven movement:

If we integrate the expression ds=vdt over time in the range from t to t+Δt (see formula (2)), we will find the length of the path traveled by the point during the time Δt:

In the case of uniform motion, the numerical value of the instantaneous speed is constant; Then expression (3) will take the form

The length of the path traveled by a point during the time period from t1 to t2 is given by the integral

ACCELERATION

When driving unevenly, it is often necessary to know how quickly the speed changes over time. A physical quantity that characterizes the rate of change in speed in magnitude and direction is called acceleration. Let us consider plane motion - motion in which the trajectories of each point of the system under consideration lie in the same plane. Let vector v be the speed of point A at time t. During the time Δt, the point moved to position B and received a speed different from v both in magnitude and direction and equal to v1 + Δv. Let's move the vector v1 to point A and find Δv (Fig. 1).

The average acceleration of uneven motion in the interval from t to t+Δt is a vector quantity equal to the ratio of the change in speed Δv to the time interval Δt:

The instantaneous acceleration a (acceleration) of a material point at time t will be a vector quantity:

equal to the first derivative of speed with respect to time.

Let us decompose the vector Δv into two components. To do this, from point A (Fig. 1) in the direction of velocity v, we plot the vector AD, whose modulus is equal to v1. Obviously, the CD vector equal to Δvτ determines the change in speed over time Δt modulo: Δvτ=v1-v. The second component Δvn of the vector Δv characterizes the change in speed over time Δt in direction.

Tangential component of acceleration:

i.e., it is equal to the first derivative with respect to time of the speed modulus, thereby determining the rate of change of speed in modulus.

We are looking for the second component of acceleration. We assume that point B is very close to point A, so Δs can be considered an arc of a circle of some radius r, slightly different from the chord AB. The triangle AOB is similar to the triangle EAD, from which it follows Δvn/AB=v1/r, but since AB=vΔt, then

In the limit at Δt→0 we obtain v1→v.

Because v1→v, angle EAD tends to zero, and since triangle EAD is isosceles, then the angle ADE between v and Δvn tends to a right angle. Consequently, at Δt→0 the vectors Δvn and v become mutually perpendicular. Because the velocity vector is directed tangentially to the trajectory, then the vector Δvn, perpendicular to the velocity vector, is directed to the center of curvature of the point’s trajectory. The second component of acceleration, equal to

is called the normal component of acceleration and is directed along a straight line perpendicular to the tangent to the trajectory (called the normal) to the center of its curvature (therefore it is also called centripetal acceleration).

The total acceleration of the body is the geometric sum of the tangential and normal components (Fig. 2):

This means that the tangential component of acceleration is a characteristic of the rate of change in speed in absolute value (directed tangentially to the trajectory), and the normal component of acceleration is a characteristic of the rate of change of speed in direction (directed towards the center of curvature of the trajectory). Depending on the tangential and normal components of acceleration, motion can be classified as follows:

1)aτ=0, an=0 - rectilinear uniform motion;

2)aτ=an=const, аn=0 - rectilinear uniform motion. With this type of movement

If the initial time t1 = 0, and the initial speed v1 = v0, then, denoting t2=t and v2 = v, we obtain a=(v-v0)/t, from which

Having integrated this formula over the range from zero to an arbitrary moment of time t, we find that the length of the path traveled by a point in the case of uniformly variable motion

3)aτ=f(t), an=0 - rectilinear motion with variable acceleration;

4)aτ=0, an=const. When aτ=0, the speed does not change in absolute value, but changes in direction. From the formula an=v2/r it follows that the radius of curvature must be constant. Therefore, circular motion is uniform; uniform curvilinear motion;

5)aτ=0, an≠0 uniform curvilinear motion;

6)aτ=const, an≠0 - curvilinear uniform motion;

7)aτ=f(t), an≠0 - curvilinear motion with variable acceleration.

No. 18 Equations of the tangent plane and normal to the surface

Definition. Let a function of two variables z =f(x,y) be given on a domain D, M0(x0;y0) is an internal point of the domain D, M(x0+Δx;y+Δy) is a point in D “neighboring” M0.

Consider the full increment of the function:

If Δz is represented as:

where A, B are constants (independent of Δx, Δy), - distance between M and M0, α(Δ x,Δy) - infinitesimal at Δx 0, Δy 0; then the function z =f(x,y) is called differentiable at the point M0, and the expression

is called the total differential of the function z =f(x;y) at the point M0.

Theorem 1.1. If z =f(x;y) is differentiable at the point M0, then

Proof

Since in (1.16) Δx, Δy are arbitrary infinitesimals, we can take Δy =0, Δx≠0, Δx 0, then

after which from (1.16) it follows

Similarly, it is proved that

and Theorem 1.1. proven.

Note: the differentiability of z =f(x,y) at the point M0 implies the existence of partial derivatives. The converse statement is false (the existence of partial derivatives at the point M0 does not imply differentiability at the point M0).

As a result, taking into account Theorem 1.1, formula (1.18) will take the form:

Consequence. A function differentiable at the point M0 is continuous at this point (since from (1.17) it follows that for Δx 0, Δy 0: Δz 0, z(M) z(M0)).

Note: Similarly for the case of three or more variables. Expression (1.17) will take the form:

Using the geometric meaning (Fig. 1.3) of partial derivatives, we can obtain the following equation (1.24) of the tangent plane πcass to the surface: z =f(x,y) at point C0(x0,y0,z0), z0=z(M):

From a comparison of (1.24) and (1.21) we obtain the geometric meaning of the total differential of a function of two variables:

Increment of applicate z when point C moves along a tangent plane from point C0 to point

where is from (1.24).

The equation of the normal Lн to the surface: z = f(x,y) at point C0 is obtained as the equation of a straight line passing through C0 perpendicular to the tangent plane:

No. 19 Directional derivative. Gradient

Let a function be given in some domain and period . Let us draw a vector from the point whose direction cosines . On the vector, at a distance from its beginning, consider a point, i.e. .

We will assume that the function and its first-order partial derivatives are continuous in the domain.

The limit of the ratio at is called the derivative of the function at the point in the direction of the vector and is denoted, i.e. .

To find the derivative of a function at a given point in the direction of the vector use the formula:

Where – direction cosines of the vector , which are calculated by the formulas:
.

Let a function be specified at each point of a certain region .

A vector whose projections on the coordinate axes are the values ​​of the partial derivatives of this function at the corresponding point is called the gradient of the function and is designated or (read “nabla u”): .

In this case, they say that a vector field of gradients is defined in the region.

To find the gradient of a function at a given point use the formula: .

No. 22 basic properties of the indefinite integral

Indefinite integral

where F is the antiderivative of the function f (on the interval); C is an arbitrary constant.

Basic properties

1.

2.

3. If That

24)

25)

28)

This method is used in cases where the integrand is a product or quotient of heterogeneous functions. In this case, V’(x) is taken to be the part that is easily integrated.

29)

32) Decomposition of a rational fraction into simple fractions.

Any proper rational fraction
can be represented as the sum of a finite number of simple rational fractions of the first – fourth types. For decomposition
it is necessary to expand the denominator into simple fractions Qm(x) into linear and square factors, for which you need to solve the equation:

- (5)

Theorem.Proper rational fraction
, Where
, can be uniquely decomposed into a sum of simple fractions:

- (6)

(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – some real numbers).

33) Decomposition of a proper fraction into simple fractions with complex roots of the denominator

Formulation of the problem. Find the indefinite integral

1 . Let us introduce the following notation:

Let's compare the degrees of the numerator and denominator.

If the integrand is an improper rational fraction, i.e. numerator degreen greater than or equal to the power of the denominatorm , then first we select the whole part of the rational function by dividing the numerator by the denominator:

Here the polynomial is the remainder of division by and the degreePk(x) less degreeQm

2 . Let's expand the proper rational fraction

to elementary fractions.

If its denominator has simple complex roots i.e.

then the expansion has the form

3 . To calculate uncertain coefficients,A1,A2,A3...B1,B1,B3... we bring the fraction on the right side of the identity to a common denominator, after which we equate the coefficients at the same powersX in the numerators on the left and right. Let's get the system 2 S equations with 2 S unknown, which has a unique solution.

4 We integrate elementary fractions of the form

47) If there is a finite limit I of the integral sum as λ → 0, and it does not depend on the method of choosing points ξ i, the method of partitioning the segment, then this limit is called the definite integral of the function f (x) over the segment and is denoted as follows:

In this case, the function f (x) is said to be integrable on . The numbers a and b are called the lower and upper limits of integration, respectively, f (x) is the integrand, x is the variable of integration. It should be noted that it does not matter which letter denotes the integration variable of a definite integral

since changing notations of this kind does not in any way affect the behavior of the integral sum. Despite the similarity in notation and terminology, definite and indefinite integrals are different

48) Theorem on the existence of a definite integral

Let's divide the segment into parts by points x1,x2,x3... so

Let us denote by deltaX the length of the i-th piece and by the maximum of these lengths.

Let us arbitrarily select a certain point on each segment so that (it is called the “midpoint”), and compose

a quantity called the integral sum

Let's find the limit now

Definition. If it exists and it does not depend on

a) the method of dividing a segment into parts and from

b) method for choosing the midpoint,

is a definite integral of the function f(x) over the segment .

The function f(x) is called in this case integrable on the interval. The quantities a and b are called the lower and upper limits of integration, respectively.

50) Basic properties of a definite integral

1) If the integration interval is divided into a finite number of partial intervals, then the definite integral taken over the interval is equal to the sum of definite integrals taken over all its partial intervals.

2) the mean value theorem.

Let the function y = f(x) be integrable on the interval ,m=min f(x) and M=max f(x), then there exists such a number

Consequence.

If the function y = f(x) is continuous on the interval , then there is a number such that.

3) When rearranging the limits of integration, the definite integral changes its sign to the opposite.

4) A definite integral with the same limits of integration is equal to zero.

5)Integration of function module

If the function f(x) is integrable, then its module is also integrable on the interval.

6)Integration of inequality

If f(x) and q(x) are integrable on an interval and x belongs to

That

7)Linearity

The constant factor can be taken beyond the sign of the definite integral

if f(x) exists and is integrable on the interval, A=const

If the function y=f(x) is continuous on an interval and F(x) is any of its antiderivatives on (F’(x)=f(x)), then the formula holds

Let the substitution x=α(t) be made to calculate the integral of a continuous function.

1) The function x=α(t) and its derivative x’=α’(t) are continuous for t belonging to

2) The set of values ​​of the function x=α(t) at t belongs to the segment

3) A α(c)=a and α(v)=b

Let the function f(x) be continuous on the interval and have an infinite discontinuity at x=b. If a limit exists, then it is called an improper integral of the second kind and is denoted by .

Thus, by definition,

If the limit on the right hand side exists, then the improper integral converges. If the specified limit does not exist or is infinite, then they say that the integral diverges.

Definition 1. Vector g is called a vector function of the scalar argument t if each value of the scalar from the range of permissible values ​​corresponds to a certain value of the vector r. We will write it like this: If the vector r is a function of the scalar argument t then the coordinates x, y, z of the vector r are also will be functions of the argument t: Vector function of the scalar argument. Hodograph. Limit and continuity of the vector function of a scalar argument. Conversely, if the coordinates of the vector g are functions of t%, then the vector g itself will be a function of t: Thus, specifying the vector function r(f) is equivalent to specifying three scalar functions y(t), z( t). Definition 2. The hodograph of a vector function r(t) of a scalar argument is the locus of points that describes the end of the vector r(*) when the scalar t changes, when the beginning of the vector r(f) is placed at a fixed point O in space (Fig. I ). Hodograph for the sake of the whisker vector r = g(*) movement Fig. 1 burning point will be the trajectory L of this point itself. The speed hodograph v = v(J) of this point will be some other line L\ (Fig. 2). So, if a material point moves in a circle with a constant speed |v| = const, then its velocity hodograph is also a circle with a center at point 0\ and with a radius equal to |v|. Example 1. Construct a hodograph of the vector r = ti + t\ + t\. Solution. 1. This construction can be done point by point, making a table: Fig. 3 2i You can do the same. Denoting the coordinates of the vector V by x, y, z, we will have Hts And key from these equations is the parameter 1Y we obtain the equations of the surfaces y - z = x1, the intersection line L of which will determine the hodograph of the vector z() (Fig. 3). D> Tasks for independent solution. Construct hodographs of vectors: Let the vector function r = scalar argument t be defined in some neighborhood of the value to of the argument t, except, perhaps, for the same value, extension 1. The constant vector А is called the limit of the vector r(t) at, if for any e > 0 there exists b > 0 such that for all t φ to satisfying condition 11, the inequality holds. As in conventional analysis, write limr(0=A. Fig. 4 Geometrically, this means that the vector) as t -* to tends to the vector And both in length and in direction (Fig. 4). Definition 2. The vector a(£) is said to be infinitesimal at t -» to if a(£) has a limit at t -* to and this limit is equal to zero: Vector function of a scalar argument. Hodograph. The limit and continuity of a vector function of a scalar argument or, which is the same, for any e there exists 6 > 0 such that for all t Ф to satisfying the condition, the inequality |a(£)| example 1. Show that the vector is an infinitely scarlet vector for t -* 0. Solution. We have where it is clear that if for any e 0 we take 6 = ~, then at -0| we will mark |. According to the definition, this means that a(t) is an infinite vector at t 0. 1> problems for solving r independently. Show that the limit of the modulus of a vector is equal to the modulus of its limit if the latter limit exists. . Prove that in order for the vector function r(*) to have a limit A, it is necessary and sufficient that r(can be represented in the form Vector function of a scalar argument. Hodograph. Limit and continuity of a vector function of a scalar argument de a( t) - move the vector endlessly for t -* t0. 14. The vector function a+ b(*) is continuous for t = t0. Does it follow from this that the vectors a(t) and b(J) are also continuous for t - to ? 15. Prove that if a( are continuous vector functions, then their scalar product (a(*),b(f)) and the vector product |a(f),b(t)] are also continuous.

Example 2. Consider, for example, a function of three variables f(X,at,z), having the following truth table:

With the lexicographic order of the vectors of variable values  X n they can be omitted and the function will be completely specified by its own vector of truth values f= (10110110).

Matrix method

The point is that many variables  X n breaks into two parts  at m And  z n–m such that all possible truth values ​​of the vector  at m are plotted along the rows of the matrix, and all possible truth values ​​of the vector  z n - m- by columns. Function truth values f on every set   n = ( 1 , ...,  m ,  m+ 1 ,...,  n) placed in the cells formed by the intersection of the line ( 1 , ...,  m) and column ( m+ 1 ,...,  n).

In Example 2 discussed above, in the case of partitioning variables ( x, y, z) into subsets ( X) And ( y, z) the matrix takes the form:

	y,z

An essential feature of the matrix method is that complete sets of variables  X n, corresponding to neighboring (both vertically and horizontally) cells, differ in one coordinate.

Specifying using a full binary tree

For description n-local function f( X n) the height property of a binary tree is used n, which consists in the fact that each pendant vertex in it corresponds one-to-one to a certain set of vector values  X n. Accordingly, this hanging vertex can be assigned the same truth value that the function has on this set f. As an example (Fig. 1.3), we present a task using a binary tree of the ternary function discussed above f =(10110110).

The first row of numbers assigned to the hanging vertices of the tree denotes the lexicographic number of the set, the second - the set itself, and the third - the value of the function on it.

Task usingn - dimensional unit cubeIN n

Since the tops IN n can also be mapped one-to-one to the set of all sets  X n, That n-local function f(X n) can be specified by assigning its truth values ​​to the corresponding vertices of the cube IN n . Figure 1.4 shows the function setting f= (10110110) in Cuba IN 3. Truth values ​​are assigned to the vertices of the cube.

Definition . Algebra of logic name a set of Boolean constants and variables along with the logical connectives introduced on them.

Formula task

Logic algebra functions can be specified as analytical expressions.

Definition. Let X― alphabet of variables and constants used in logical algebra, F― a set of notations for all elementary functions and their generalizations with a number of variables exceeding 2.

Formula over X,F(logic algebra formula) let's call all records of the form:

A) X, Where X X;

b)  F 1 , F 1 &F 2 ,F 1 F 2 , F 1 F 2 , F 1  F 2 , F 1 F 2 ,F 1 F 2 ,F 1 F 2 , Where F 1 , F 2 - formulas over X, F;

V) h(F 1 , … ,F n ), Where n > 2, F 1 ,… ,F n- formulas over X,F, h ― denotation of the generalized threshold function from F .

As follows from the definition, for two-place elementary functions the infix form of notation is used, in which the functional symbol is placed between the arguments; for negation and generalized functions, the prefix form of notation is used, in which the functional symbol is placed before the list of arguments.

Example 3.

1. Expressions X(atz); ( x, y, z  u) are formulas of the algebra of logic, since they satisfy the definition given above.

2. Expression  X (at z) is not a logical algebra formula because the operation  was applied incorrectly .

Definition. The function implemented by the formula F, is the function obtained by substituting the values ​​of variables into F. Let's denote it f(F).

Example 4. Consider the formula F=xy (Xz). In order to construct the truth table of the implemented function, it is necessary to perform logical multiplication sequentially, taking into account the strength of logical connectives xy, then the implication ( Xz), then add the resulting truth values ​​modulo 2. The result of the actions is shown in the table:

				X z

The formulaic representation of functions allows one to evaluate a priori many properties of functions. The transition from a formulaic task to a truth table can always be accomplished by successive substitutions of truth values ​​into elementary functions included in the formula. The reverse transition is ambiguous, since the same function can be represented by different formulas. It requires separate consideration.