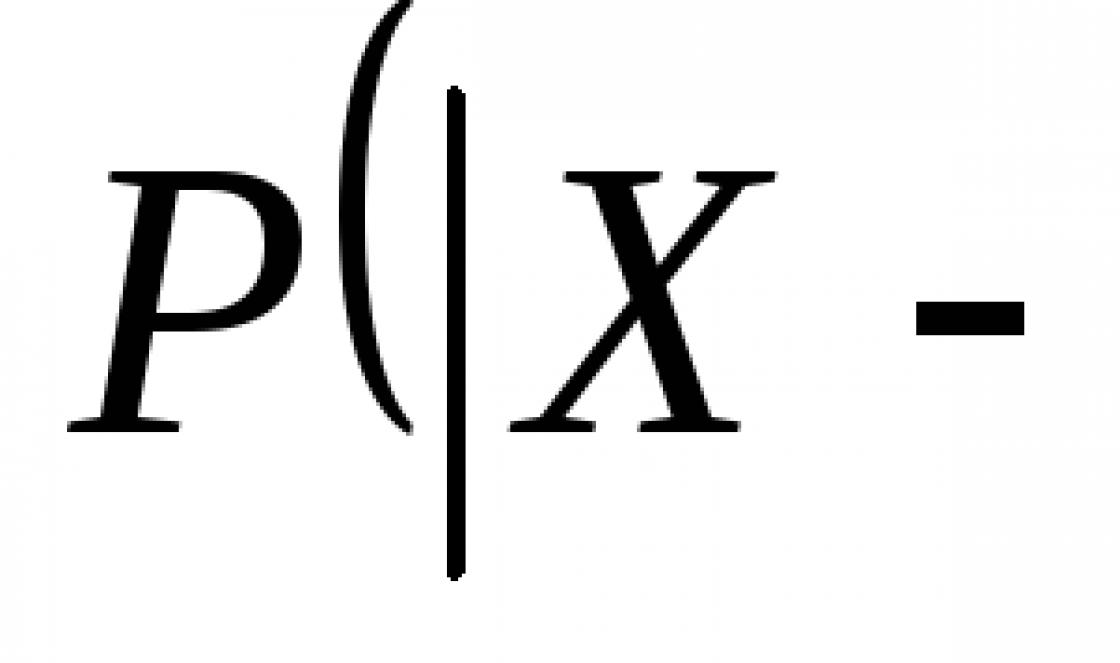A nagy számokra vonatkozó szavak a tesztek számára utalnak - egy valószínűségi változó nagyszámú értékét vagy nagyszámú valószínűségi változó kumulatív hatását vesszük figyelembe. Ennek a törvénynek a lényege a következő: bár lehetetlen megjósolni, hogy egy egyedi valószínűségi változó mekkora értéket vesz fel egyetlen kísérletben, azonban a nagyszámú független valószínűségi változó hatásának összesített eredménye elveszti véletlenszerű jellegét, és szinte megbízhatóan (azaz nagy valószínűséggel) előre jelezhető. Például lehetetlen megjósolni, hogy egy érme melyik irányba fog landolni. Ha azonban 2 tonna érmét dobunk ki, akkor nagy bizalommal kijelenthetjük, hogy a címerrel felfelé hullott érmék súlya 1 tonna.

A nagy számok törvénye elsősorban az úgynevezett Csebisev-egyenlőtlenségre vonatkozik, amely egyetlen tesztben megbecsüli, hogy egy valószínűségi változó milyen valószínűséggel fogad el egy olyan értéket, amely legfeljebb egy adott értékkel tér el az átlagos értéktől.

Csebisev egyenlőtlensége. Hadd x- tetszőleges valószínűségi változó, a=M(X) , A D(x) – szórása. Akkor

Példa. A gépen bekapcsolt hüvely átmérőjének névleges (azaz szükséges) értéke egyenlő 5 mm, és a szóródás nincs többé 0.01 (ez a gép pontossági tűrése). Becsüljük meg annak valószínűségét, hogy egy persely gyártása során az átmérőjének eltérése a névlegestől kisebb lesz, mint 0,5 mm .

Megoldás. Legyen r.v. x– a gyártott persely átmérője. A feltétel szerint a matematikai elvárása megegyezik a névleges átmérővel (ha nincs szisztematikus hiba a gépbeállításokban): a=M(X)=5 és a diszperzió D(X)≤0,01. Csebisev egyenlőtlenségének alkalmazása at ε = 0,5, kapunk:

Így egy ilyen eltérés valószínűsége meglehetősen nagy, ezért arra a következtetésre juthatunk, hogy egy alkatrész egyszeri legyártása esetén szinte biztos, hogy az átmérő eltérése a névlegestől nem haladja meg a 0,5 mm .

Jelentésében a szórás σ jellemzi átlagos egy valószínűségi változó eltérése a középpontjától (vagyis a matematikai elvárásától). Mert ez átlagos eltérés, akkor a tesztelés során nagy (a hangsúly az o-n) eltérések lehetségesek. Gyakorlatilag mekkora eltérések lehetségesek? A normál eloszlású valószínűségi változók tanulmányozásakor levezettük a „három szigma” szabályt: egy normális eloszlású valószínűségi változót. x egyetlen tesztben gyakorlatilag nem tér el tovább az átlagától, mint 3σ, Ahol σ= σ(X)– az r.v. szórása. x. Ezt a szabályt abból származtattuk, hogy megkaptuk az egyenlőtlenséget

.

Most becsüljük meg ennek valószínűségét tetszőleges valószínűségi változó x olyan értéket fogadjon el, amely az átlagtól legfeljebb a szórás háromszorosával tér el. Csebisev egyenlőtlenségének alkalmazása at ε = 3σés tekintettel arra D(Х)= σ 2 , kapunk:

.

És így, általában szám alapján megbecsülhetjük annak valószínűségét, hogy egy valószínűségi változó legfeljebb három szórással tér el az átlagától. 0.89 , míg normál eloszlás esetén ez valószínűséggel garantálható 0.997 .

A Csebisev-egyenlőtlenség független, azonos eloszlású valószínűségi változók rendszerére általánosítható.

Általános Csebisev-egyenlőtlenség. Ha független valószínűségi változók x 1 , X 2 , … , X n M(x én )= aés eltérések D(x én )= D, Azt

Nál nél n=1 ez az egyenlőtlenség átalakul a fent megfogalmazott Csebisev-egyenlőtlenséggé.

A megfelelő problémák megoldásában önálló jelentőségű Csebisev-egyenlőtlenség az ún. Csebisev-tétel bizonyítására szolgál. Először ennek a tételnek a lényegéről beszélünk, majd megadjuk a formális megfogalmazását.

Hadd x 1 , X 2 , … , X n– nagyszámú független valószínűségi változó matematikai elvárásokkal M(X 1 )=a 1 , … , M(X n )=a n. Bár egy kísérlet eredményeként mindegyik felvehet az átlagától (vagyis a matematikai elvárástól) messze eső értéket, azonban egy valószínűségi változó
, amelyek számtani átlagukkal megegyeznek, nagy valószínűséggel egy rögzített számhoz közeli értéket vesznek fel
(ez az összes matematikai elvárás átlaga). Ez a következőket jelenti. Legyen a teszt eredményeként független valószínűségi változók x 1 , X 2 , … , X n(sok van belőlük!) ennek megfelelően vett értékeket x 1 , X 2 , … , X n illetőleg. Majd ha ezek az értékek maguk is távol esnek a megfelelő valószínűségi változók átlagértékeitől, akkor az átlagértékük
nagy valószínűséggel közel lesz a számhoz
. Így nagyszámú valószínűségi változó számtani átlaga már elveszti véletlenszerűségét, és nagy pontossággal előre jelezhető. Ez azzal magyarázható, hogy az értékek véletlenszerű eltérései x én tól től a én különböző előjelűek lehetnek, és ezért összességében ezek az eltérések valószínűleg kompenzálódnak.

Terema Csebisev (nagy számok törvénye Csebisev formában). Hadd x 1 , X 2 , … , X n … – páronként független valószínűségi változók sorozata, amelyek varianciái ugyanarra a számra korlátozódnak. Ezután bármilyen kicsi ε számot veszünk, az egyenlőtlenség valószínűsége

a kívánt szám közel lesz az egyhez n Vegyünk elég nagy valószínűségi változókat. Formálisan ez azt jelenti, hogy a tétel feltételei között

Ezt a fajta konvergenciát valószínűség szerinti konvergenciának nevezik, és jelölése:

Így Csebisev tétele azt mondja, hogy ha kellően nagy számú független valószínűségi változó van, akkor azok számtani átlaga egyetlen tesztben szinte megbízhatóan a matematikai várakozásaik átlagához közeli értéket vesz fel.

A Csebisev-tételt leggyakrabban olyan helyzetekben alkalmazzák, ahol a valószínűségi változók x 1 , X 2 , … , X n … azonos eloszlásúak (azaz ugyanaz az eloszlási törvény vagy azonos valószínűségi sűrűség). Valójában ez egyszerűen ugyanazon valószínűségi változó nagy számú példánya.

Következmény(általánosított Csebisev-egyenlőtlenség). Ha független valószínűségi változók x 1 , X 2 , … , X n … azonos eloszlásúak a matematikai elvárásokkal M(x én )= aés eltérések D(x én )= D, Azt

, azaz
.

A bizonyítás az általánosított Csebisev-egyenlőtlenségből következik, a határértékhez való átlépéssel n→∞ .

Még egyszer jegyezzük meg, hogy a fentebb leírt egyenlőségek nem garantálják a mennyiség értékét
arra törekszik A nál nél n→∞. Ez a mennyiség továbbra is valószínűségi változó marad, és az egyedi értékei meglehetősen távol állnak tőle A. De ennek a valószínűsége (messze nem A) értékeket növekvő mértékben n 0-ra hajlik.

Megjegyzés. A következtetés következtetése nyilvánvalóan érvényes az általánosabb esetben is, amikor független valószínűségi változók x 1 , X 2 , … , X n … eltérő eloszlásúak, de ugyanazok a matematikai elvárások (egyenlő A) és együttesen korlátozott eltérések. Ez lehetővé teszi, hogy előre jelezzük egy bizonyos mennyiség mérésének pontosságát, még akkor is, ha ezeket a méréseket különböző műszerekkel végezték.

Tekintsük részletesebben ennek a következménynek az alkalmazását a mennyiségek mérésénél. Használjunk valamilyen eszközt n azonos mennyiség mérése, amelynek valódi értéke egyenlő Aés nem tudjuk. Az ilyen mérések eredményei x 1 , X 2 , … , X n jelentősen eltérhetnek egymástól (és a valódi értéktől A) különböző véletlenszerű tényezők miatt (nyomásváltozások, hőmérséklet, véletlenszerű rezgés stb.). Tekintsük az r.v. x– műszer leolvasása mennyiség egyszeri mérésére, valamint egy sor r.v. x 1 , X 2 , … , X n– műszer leolvasása az első, második, ..., utolsó mérésnél. Így az egyes mennyiségek x 1 , X 2 , … , X n az s.v. esetei közül csak egy van. x, és ezért mindegyiknek ugyanaz az eloszlása, mint az r.v. x. Mivel a mérési eredmények nem függnek egymástól, így az r.v. x 1 , X 2 , … , X n függetlennek tekinthető. Ha a készülék nem produkál szisztematikus hibát (például a skála nullája nincs „kikapcsolva”, a rugó nincs megfeszítve stb.), akkor feltételezhetjük, hogy a matematikai elvárás M(X) = a, és ezért M(X 1 ) = ... = M(X n ) = a. Így a fenti következmény feltételei teljesülnek, tehát a mennyiség közelítő értékeként A egy valószínűségi változó „realizációját” vehetjük fel
kísérletünkben (amely egy sorozat végrehajtásából áll n mérések), azaz.

.

Nagyszámú mérés mellett gyakorlatilag biztos a jó számítási pontosság ezzel a képlettel. Ez indokolja azt a gyakorlati elvet, hogy nagy számú mérés mellett ezek számtani átlaga gyakorlatilag nem sokban tér el a mért érték valódi értékétől.

A matematikai statisztikában széles körben használt „mintavételi” módszer a nagy számok törvényén alapul, amely lehetővé teszi, hogy egy valószínűségi változó viszonylag kis mintájából elfogadható pontossággal megkapjuk objektív jellemzőit. De erről a következő részben lesz szó.

Példa. Egy bizonyos mennyiséget olyan mérőeszközön mérnek, amely nem okoz szisztematikus torzítást A egyszer (kapott értéket x 1 ), majd további 99 alkalommal (megszerzett értékek x 2 , … , X 100 ). A valódi mérési értékhez A először az első mérés eredményét veszik fel
, majd az összes mérés számtani középértéke
. A készülék mérési pontossága olyan, hogy a mérés szórása σ legfeljebb 1 (ezért a szórás D=σ 2 szintén nem haladja meg az 1-et). Minden mérési módszernél becsülje meg annak valószínűségét, hogy a mérési hiba nem haladja meg a 2-t.

Megoldás. Legyen r.v. x– műszer leolvasása egyetlen méréshez. Aztán feltételek szerint M(X)=a. A feltett kérdések megválaszolásához az általánosított Csebisev-egyenlőtlenséget alkalmazzuk

ε-nél =2 először azért n=1 majd azért n=100 . Az első esetben azt kapjuk
, és a másodikban. Így a második eset gyakorlatilag garantálja a megadott mérési pontosságot, míg az első ilyen értelemben nagy kétségeket hagy maga után.

Alkalmazzuk a fenti állításokat a Bernoulli-sémában felmerülő valószínűségi változókra. Emlékezzünk vissza ennek a rendszernek a lényegére. Hagyd előállítani n független kísérletek, amelyek mindegyike tartalmaz valamilyen eseményt A azonos valószínűséggel jelenhetnek meg R, A q=1–р(értelemszerűen ez az ellenkező esemény valószínűsége - az esemény nem következik be A) . Töltsünk el egy kis számot n ilyen tesztek. Nézzük a véletlen változókat: x 1 – az esemény előfordulásának száma A V 1 -próba,..., x n– az esemény előfordulásának száma A V n-a teszt. Minden beírt sz.v. értékeket vehet fel 0 vagy 1 (esemény A megjelenhet a tesztben, vagy nem), és az érték 1 feltételnek megfelelően minden próbában valószínűséggel elfogadják p(az esemény bekövetkezésének valószínűsége A minden kísérletben), és az értéket 0 valószínűséggel q= 1 – p. Ezért ezeknek a mennyiségeknek ugyanazok az eloszlási törvényei:

x 1

x n

Ezért ezen mennyiségek átlagértékei és szórásaik is megegyeznek: M(X 1 )=0 ∙ q+1 ∙ p= p, …, M(X n )= p ; D(x 1 )=(0 2 ∙ q+1 2 ∙ p)− p 2 = p∙(1− p)= p ∙ q, … , D(x n )= p ∙ q. Ha ezeket az értékeket behelyettesítjük az általánosított Csebisev-egyenlőtlenségbe, azt kapjuk

.

Egyértelmű, hogy az r.v. x=x 1 +…+X n az esemény előfordulásának száma A mindenben n tesztek (ahogy mondják - „a sikerek száma” a n tesztek). Engedd be a levezényelt n tesztelő esemény A megjelent k tőlük. Ekkor az előző egyenlőtlenség így írható fel

.

De a nagyságrend
, egyenlő az esemény előfordulásai számának arányával A V n a független kísérleteket a kísérletek teljes számához képest korábban relatív eseménygyakoriságnak nevezték A V n tesztek. Ezért egyenlőtlenség van

.

Most fordulva a határértékre: n→∞, azt kapjuk
, azaz
(valószínűség szerint). Ez alkotja a nagy számok törvényének tartalmát Bernoulli formában. Ebből az következik, hogy kellően nagy számú teszttel n a relatív gyakoriság tetszőlegesen kis eltérései
az eseményeket annak valószínűségétől R- szinte megbízható események, és nagy eltérések - szinte lehetetlen. Az ebből eredő következtetés a relatív frekvenciák ilyen stabilitásáról (amelyről korábban úgy beszéltünk, mint kísérleti tény) egy esemény valószínűségének korábban bevezetett statisztikai definícióját olyan számként indokolja, amely körül egy esemény relatív gyakorisága ingadozik.

Tekintettel arra, hogy a kifejezés p∙ q= p∙(1− p)= p− p 2 nem haladja meg a változási intervallumot
(ez könnyen ellenőrizhető, ha ezen a szegmensen megtaláljuk ennek a függvénynek a minimumát), a fenti egyenlőtlenségből
könnyű megszerezni

,

amelyet a releváns problémák megoldására használnak (az egyiket az alábbiakban közöljük).

Példa. Az érmét 1000-szer dobták fel. Becsüljük meg annak valószínűségét, hogy a címer megjelenésének relatív gyakoriságának a valószínűségétől való eltérése kisebb lesz 0,1-nél!

Megoldás. Egyenlőtlenség alkalmazása
nál nél p= q=1/2 , n=1000 , ε=0,1, megkapjuk .

Példa. Becsülje meg annak valószínűségét, hogy az előző példa feltételei mellett a szám k leejtett emblémák a tartományban lesznek 400 előtt 600 .

Megoldás. Feltétel 400< k<600 azt jelenti, hogy 400/1000< k/ n<600/1000 , azaz 0.4< W n (A)<0.6 vagy
. Amint az előző példából láttuk, egy ilyen esemény valószínűsége nem kisebb 0.975 .

Példa. Valamely esemény valószínűségének kiszámítása A 1000 kísérletet végeztek, amelyben az esemény A 300 alkalommal jelent meg. Becsülje meg annak valószínűségét, hogy a relatív gyakoriság (300/1000 = 0,3) eltér a valódi valószínűségtől R legfeljebb 0,1.

Megoldás. A fenti egyenlőtlenség alkalmazása
ha n=1000, ε=0,1, akkor .

A nagy számok törvénye a valószínűségszámításban azt állítja, hogy egy fix eloszlásból származó kellően nagy véges minta tapasztalati átlaga (számtani átlaga) közel van ennek az eloszlásnak az elméleti átlagához (matematikai várakozás). A konvergencia típusától függően különbséget teszünk a nagy számok gyenge törvénye között, amikor a konvergencia valószínűséggel következik be, és a nagy számok erős törvénye között, amikor a konvergencia szinte mindenhol előfordul.

Mindig van véges számú próba, amelyben bármilyen előrelépési valószínűség mellett kevesebb van 1 valamely esemény relatív előfordulási gyakorisága a lehető legkisebb mértékben fog eltérni annak valószínűségétől.

A nagy számok törvényének általános jelentése: nagyszámú azonos és független véletlentényező együttes hatása olyan eredményre vezet, amely határértékben nem a véletlentől függ.

A véges mintaelemzésen alapuló valószínűségbecslési módszerek ezen a tulajdonságon alapulnak. Jó példa erre a választási eredmények előrejelzése a választói mintán végzett felmérés alapján.

Enciklopédiai YouTube

1 / 5

✪ A nagy számok törvénye

✪ 07 – Valószínűségszámítás. A nagy számok törvénye

✪ 42 A nagy számok törvénye

✪ 1 – Csebisev nagy számok törvénye

✪ 11. évfolyam, 25. lecke, Gauss-görbe. A nagy számok törvénye

Feliratok

Nézzük meg a nagy számok törvényét, amely talán a legintuitívabb törvény a matematikában és a valószínűségszámításban. És mivel nagyon sok mindenre vonatkozik, néha használják és félreértik. Hadd definiáljam először a pontosság kedvéért, majd az intuícióról beszélünk. Vegyünk egy valószínűségi változót, például X. Tegyük fel, hogy ismerjük a matematikai elvárását vagy a sokaság átlagát. A nagy számok törvénye egyszerűen azt mondja, hogy ha veszünk egy példát egy valószínűségi változó n-edik számú megfigyelésére, és vesszük az összes megfigyelés átlagát... Vegyünk egy változót. Nevezzük X-nek egy n alsó indexszel és egy oszloppal a tetején. Ez a valószínűségi változónk n-edik számú megfigyelésének számtani átlaga. Íme az első észrevételem. Egyszer megcsinálom a kísérletet, és elvégzem ezt a megfigyelést, aztán megismétlem, és elvégzem ezt a megfigyelést, és újra megcsinálom, és megkapom ezt. Ezt a kísérletet az n-edik alkalommal végzem el, majd elosztom a megfigyeléseim számával. Itt van a mintaátlagom. Itt van az általam végzett összes megfigyelés átlaga. A nagy számok törvénye azt mondja, hogy a minta átlaga megközelíti a valószínűségi változó várható értékét. Vagy azt is leírhatom, hogy a mintaátlagom megközelíti a végtelenbe hajló n-edik mennyiség populációs átlagát. Nem teszek egyértelmű különbséget a "közelítés" és a "konvergencia" között, de remélem, intuitívan megértitek, hogy ha itt elég nagy mintát veszek, akkor a populáció egészére nézve megkapom a várható értéket. Azt hiszem, a legtöbben intuitív módon megértik, hogy ha elég sok tesztet végzek el sok példával, akkor végül a tesztek azt az értékeket fogják megadni, amelyeket várok, figyelembe véve a várható értéket, valószínűséget és mindezt a jazzt. De azt hiszem, gyakran nem világos, hogy ez miért történik. És mielőtt elmagyaráznám, miért van ez így, hadd mondjak egy konkrét példát. A nagy számok törvénye azt mondja nekünk, hogy... Tegyük fel, hogy van egy X valószínűségi változó. Ez egyenlő a fejek számával egy tisztességes érme 100 feldobásakor. Először is ismerjük ennek a valószínűségi változónak a matematikai elvárását. Ez az érmefeldobások vagy próbák száma szorozva bármely próba sikerének esélyével. Tehát ez egyenlő 50-nel. Vagyis a nagy számok törvénye azt mondja, hogy ha mintát veszünk, vagy ha átlagolom ezeket a próbákat, akkor kapok. .. Amikor először csinálok tesztet, feldobok egy érmét 100-szor, vagy veszek egy dobozt száz érmével, megrázom, majd megszámolom, hány fejet kapok, és kapok, mondjuk , az 55-ös szám. Ez X1 lenne. Ezután újra megrázom a dobozt, és megkapom a 65-ös számot. Aztán megint és 45-öt kapok. És ezt n-szer megcsinálom, majd elosztom a próbálkozások számával. A nagy számok törvénye azt mondja nekünk, hogy ez az átlag (az összes megfigyelésem átlaga) megközelíti az 50-et, amikor n közeledik a végtelenhez. Most egy kicsit arról szeretnék beszélni, hogy miért történik ez. Sokan úgy gondolják, hogy ha 100 próba után átlagon felüli az eredményem, akkor a valószínűségi törvények szerint több-kevesebb fejet kell kapnom ahhoz, hogy úgymond kompenzáljam a különbséget. Nem pontosan ez fog történni. Ezt gyakran "szerencsejátékos tévedésnek" nevezik. Hadd mutassam meg a különbséget. A következő példát használom. Hadd rajzoljak egy grafikont. Változtassuk meg a színt. Ez n, az én x tengelyem n. Ennyi tesztet fogok elvégezni. És az Y tengelyem lesz a minta átlaga. Tudjuk, hogy ennek a tetszőleges változónak a matematikai elvárása 50. Hadd rajzoljam le. Ez 50. Térjünk vissza példánkhoz. Ha n... Az első tesztem során 55-öt kaptam, ez az átlagom. Csak egy adatbeviteli pontom van. Aztán két teszt után 65-öt kapok. Tehát az átlagom 65+55 osztva 2-vel. Ez 60. És az átlagom kicsit feljebb ment. Aztán 45-öt kaptam, ami megint csökkentette a számtani átlagomat. Nem fogok 45-öt ábrázolni. Most mindezt átlagolnom kell. Mit jelent 45+65? Hadd számítsam ki ezt az értéket a pont ábrázolásához. Ez 165 osztva 3-mal. Ez 53. Nem, 55. Tehát az átlag visszamegy 55-re. Folytathatjuk ezeket a teszteket. Miután elvégeztünk három próbát, és megkaptuk ezt az átlagot, sokan azt gondolják, hogy a valószínűségi istenek gondoskodnak arról, hogy a jövőben kevesebb fejet kapjunk, és hogy a következő néhány próba alacsonyabb pontszámmal csökkenti az átlagot. De ez nem mindig van így. A jövőben a valószínűség mindig ugyanaz marad. Mindig 50% az esélye annak, hogy fejet kapok. Nem arról van szó, hogy kezdetben bizonyos számú fejet kapok, többet, mint amire számítottam, aztán hirtelen farkat kell kapnom. Ez a szerencsejátékos tévedése. Csak azért, mert aránytalanul sok fejet kap, nem jelenti azt, hogy egy ponton aránytalanul sok farok fog megjelenni. Ez nem teljesen igaz. A nagy számok törvénye azt mondja, hogy ez nem számít. Tegyük fel, hogy bizonyos véges számú teszt után az átlagod... Ennek elég kicsi a valószínűsége, de ennek ellenére... Tegyük fel, hogy az átlagod elérte ezt a 70-et. Azt gondolja: "Hűha, eltávolodtunk az elvárt értéktől." De a nagy számok törvénye szerint nem mindegy, hány tesztet végzünk. Még mindig végtelen számú kihívás áll előttünk. Ennek a végtelen számú próbának a matematikai elvárása, különösen egy ilyen helyzetben, a következő lenne. Amikor egy véges számhoz érünk, amely valamilyen nagy értéket fejez ki, egy végtelen szám, amely konvergál vele, ismét a várt értékhez vezet. Ez persze nagyon laza értelmezés, de ezt mondja nekünk a nagy számok törvénye. Fontos. Nem arról van szó, hogy ha sok fejet kapunk, akkor valahogy megnő annak a valószínűsége, hogy farokot kapunk, hogy ezt kompenzálja. Ez a törvény azt mondja nekünk, hogy nem számít, mi lesz véges számú kísérlet eredménye, amíg még végtelen számú próba van hátra. És ha eleget tesz belőlük, akkor ismét a várt értéket éri el. Ez egy fontos szempont. Gondold át. De ezt nem mindennap alkalmazzák a gyakorlatban lottónál és kaszinónál, pedig köztudott, hogy ha elég tesztet csinálsz... Akár ki is számolhatjuk... mennyi a valószínűsége, hogy komolyan eltérünk a normától? De a kaszinók és a lottó minden nap azon az elven működnek, hogy ha elég embert viszel be, természetesen rövid időn belül, kis mintával, akkor néhány ember megüti a főnyereményt. De hosszú időn keresztül a kaszinó mindig nyer az általa játszani kívánt játékok paraméterei miatt. Ez egy fontos valószínűségi elv, amely intuitív. Bár néha, amikor ezt formálisan véletlenszerű változókkal magyarázzák el, mindez kissé zavarónak tűnik. Ez a törvény csak annyit mond, hogy minél több minta van, annál inkább a minták számtani átlaga a valódi átlaghoz fog igazodni. És hogy pontosabbak legyünk, a minta számtani középértéke konvergál a valószínűségi változó matematikai elvárásával. Ez minden. Találkozunk a következő videóban!

A nagy számok gyenge törvénye

A nagy számok gyenge törvényét Bernoulli tételének is nevezik Jacob Bernoulli után, aki 1713-ban bebizonyította.

Legyen egy végtelen sorozat (szekvenciális felsorolás) azonos eloszlású és nem korrelált valószínűségi változókból. Vagyis a kovarianciájuk c o v (X i , X j) = 0, ∀ i ≠ j (\displaystyle \mathrm (cov) (X_(i),X_(j))=0,\;\all i\not =j). Hadd . Jelöljük az első mintaátlagával n (\displaystyle n) tagok:

.

Akkor X ¯ n → P μ (\displaystyle (\bar (X))_(n)\to ^(\!\!\!\!\!\!\mathbb (P) )\mu ).

Vagyis bármilyen pozitívumra ε (\displaystyle \varepsilon)

lim n → ∞ Pr (| X ¯ n − μ |< ε) = 1. {\displaystyle \lim _{n\to \infty }\Pr \!\left(\,|{\bar {X}}_{n}-\mu |<\varepsilon \,\right)=1.}

A nagy számok megerősített törvénye

Legyen független azonos eloszlású valószínűségi változók végtelen sorozata ( X i ) i = 1 ∞ (\displaystyle \(X_(i)\)_(i=1)^(\infty )), egy valószínűségi téren definiálva (Ω , F , P) (\displaystyle (\Omega ,(\mathcal (F)),\mathbb (P))). Hadd E X i = μ , ∀ i ∈ N (\displaystyle \mathbb (E) X_(i)=\mu ,\;\all i\in \mathbb (N) ). Jelöljük azzal X ¯ n (\displaystyle (\bar (X))_(n)) minta átlaga első n (\displaystyle n) tagok:

X ¯ n = 1 n ∑ i = 1 n X i , n ∈ N (\displaystyle (\bar (X))_(n)=(\frac (1)(n))\sum \limits _(i= 1)^(n)X_(i),\;n\in \mathbb (N) ).

Akkor X ¯ n → μ (\displaystyle (\bar (X))_(n)\to \mu ) majdnem mindig.

Pr (lim n → ∞ X ¯ n = μ) = 1. (\displaystyle \Pr \!\left(\lim _(n\to \infty )(\bar (X))_(n)=\mu \ jobb)=1.) .

Mint minden matematikai törvény, a nagy számok törvénye is csak bizonyos feltevések mellett alkalmazható a való világra, amelyek csak bizonyos fokú pontossággal teljesíthetők. Például az egymást követő vizsgálati feltételek gyakran nem tarthatók fenn a végtelenségig és abszolút pontossággal. Ráadásul a nagy számok törvénye csak arról beszél lehetetlenség az átlagérték jelentős eltérése a matematikai elvárástól.

NAGY SZÁMOK TÖRVÉNYE

általános elv, amelynek értelmében a véletlenszerű tényezők kombinációja bizonyos nagyon általános feltételek mellett a véletlentől szinte független eredményhez vezet. Egy véletlenszerű esemény előfordulási gyakoriságának konvergenciája annak valószínűségével a próbák számának növekedésével (amit először nyilvánvalóan a szerencsejátékban vettek észre) első példaként szolgálhat ennek az elvnek a működésére.

A 17. és 18. század fordulóján. J. Bernoulli bebizonyított egy tételt, amely szerint független kísérletek sorozatában, amelyek mindegyikében egy bizonyos esemény bekövetkezése azonos értékű, a következő összefüggés igaz:

bármely - az esemény előfordulásának száma az első próbákban, - az előfordulások gyakorisága. Ez Bernoulli tétele S. Poisson kiterjesztette a független kísérletek sorozatának esetére, ahol az A esemény bekövetkezésének valószínűsége függhet a kísérletek számától. Legyen ez a k-edik próba valószínűsége egyenlő és legyen

Akkor Poisson-tétel azt állítja

mindenre Ennek a tételnek az első szigorú megközelítését P. L. Csebisev (1846) adta meg, akinek módszere teljesen eltér Poisson módszerétől, és bizonyos szélsőséges megfontolásokon alapul; S. Poisson a (2)-t a megadott valószínűség közelítő képletéből származtatta, amely Gauss-törvényen alapult, és akkor még nem volt szigorúan alátámasztva. S. Poisson találkozott először a „nagy számok törvénye” kifejezéssel, amelyet Bernoulli tételének általánosításának nevezett.

Bernoulli és Poisson tételeinek természetes további általánosítása adódik, ha észrevesszük, hogy a valószínűségi változók összegként is ábrázolhatók.

független valószínűségi változók, ahol ha A megjelenik az Ath-próbában, és - másképp. Ugyanakkor matematikai a várakozás (amely egybeesik a matematikai elvárások számtani átlagával) egyenlő p-vel Bernoulli és Poisson esetére. Vagyis mindkét esetben a számtani átlag eltérését vesszük figyelembe X k a számtani átlaguktól a matematikai elvárások.

P. L. Csebisev „Átlagos értékek” című munkájában (1867) megállapították, hogy a független valószínűségi változók esetében a kapcsolat

(bármely ) nagyon általános feltételezések szerint igaz. P. L. Csebisev feltételezte, hogy a matematikus. az elvárásokat ugyanaz a konstans határolja, bár az ő bizonyítása alapján egyértelmű, hogy a korlátos eltérések követelménye elegendő

vagy akár követeli

Így P. L. Csebisev megmutatta a Bernoulli-tétel széles körű általánosításának lehetőségét. A. A. Markov tudomásul vette a további általánosítások lehetőségét, és javasolta a B. h.z. elnevezés használatát. a Bernoulli-tétel általánosításainak teljes halmazára [és különösen a (3)-ra]. Csebisev módszere a matematika általános tulajdonságainak pontos megállapításán alapul. elvárásokról és az ún. Csebisev egyenlőtlenségek[a (3) valószínűséghez az alak becslését adja

ez a határ természetesen pontosabbra cserélhető, jelentősebb korlátozások mellett, ld Bernstein egyenlőtlenség]. A B. h.z. különféle formáinak utólagos bizonyítékai. ilyen vagy olyan mértékben a Csebisev-módszer továbbfejlesztése. A valószínűségi változók megfelelő „kivágását” alkalmazva (kicserélve azokat segédváltozókra, nevezetesen: , ha hol vannak bizonyos állandók), A. A. Markov kiterjesztette a B. részt. olyan esetekre, amikor a kifejezések eltérései nem léteznek. Például megmutatta, hogy a (3) akkor következik be, ha bizonyos konstansokra és mindenki és

Ne veszítsd el. Iratkozzon fel, és e-mailben megkapja a cikk linkjét.

Munka vagy tanulás során a számokkal és figurákkal naponta interakcióban sokan nem is sejtik, hogy létezik a nagy számoknak egy nagyon érdekes törvénye, amelyet például a statisztika, a közgazdaságtan, sőt a pszichológiai és pedagógiai kutatások is használnak. Valószínűség-elméletre hivatkozik, és azt mondja, hogy egy rögzített eloszlásból származó bármely nagy minta számtani átlaga közel van ennek az eloszlásnak a matematikai elvárásához.

Valószínűleg észrevette, hogy ennek a törvénynek a lényegét nem könnyű megérteni, különösen azok számára, akik nem túl jók a matematikában. Ez alapján szeretnénk egyszerű nyelven beszélni róla (persze lehetőség szerint), hogy mindenki legalább nagyjából magától értse, miről van szó. Ez a tudás segít jobban megérteni néhány matematikai mintát, tanultabbá válni, és pozitív hatással lesz rájuk.

A nagy számok törvényének fogalmai és értelmezése

A nagy számok törvényének fentebb tárgyalt valószínűségszámítási definíciója mellett közgazdasági értelmezését is megadhatjuk. Ebben az esetben azt az elvet képviseli, hogy egy adott típusú pénzügyi veszteség gyakorisága nagy biztonsággal előre jelezhető, ha általában magas a hasonló típusú veszteségek szintje.

Emellett a jelek konvergencia szintjétől függően nagy számok gyenge és erős törvényeit különböztethetjük meg. Gyengéről akkor beszélünk, ha a konvergencia valószí- nűséggel létezik, és erősről, ha szinte mindenben konvergencia létezik.

Ha valamelyest másképp értelmezzük, akkor azt kell mondanunk: mindig lehet találni véges számú próbát, ahol bármely előre beprogramozott, egynél kisebb valószínűséggel valamely esemény bekövetkezésének relatív gyakorisága nagyon kevéssé fog eltérni annak valószínűségétől.

Így a nagy számok törvényének általános lényege a következőképpen fejezhető ki: nagyszámú azonos és független véletlenszerű tényező komplex hatásának eredménye olyan eredmény lesz, amely nem függ a véletlentől. És még egyszerűbben fogalmazva, akkor a nagy számok törvényében a tömegjelenségek mennyiségi mintázata csak akkor jelenik meg egyértelműen, ha nagy a számuk (ezért hívják a törvényt a nagy számok törvényének).

Ebből arra következtethetünk, hogy a törvény lényege az, hogy a tömeges megfigyeléssel kapott számokban vannak olyan helyességek, amelyek kisszámú tényben nem mutathatók ki.

A nagy számok törvényének lényege és példái

A nagy számok törvénye a véletlen és a szükséges legáltalánosabb törvényeit fejezi ki. Amikor a véletlen eltérések „kioltják” egymást, az azonos szerkezetre meghatározott átlagos mutatók tipikusak formáját öltik. Lényeges és állandó tények cselekedeteit tükrözik meghatározott idő- és helyviszonyok között.

A nagy számok törvénye által meghatározott minták csak akkor erősek, ha tömegtrendet képviselnek, és nem lehetnek egyedi esetek törvényei. Így életbe lép a matematikai statisztika elve, miszerint számos véletlenszerű tényező komplex hatása nem véletlenszerű eredményt okozhat. Ennek az elvnek a működésére pedig a legszembetűnőbb példa egy véletlenszerű esemény előfordulási gyakoriságának és valószínűségének konvergenciája a kísérletek számának növekedésével.

Emlékezzünk a szokásos érmefeldobásra. Elméletileg a fejek és a farok ugyanolyan valószínűséggel eshetnek le. Ez azt jelenti, hogy ha például 10-szer feldob egy érmét, akkor 5-nek fejjel kell feljönnie, 5-nek pedig fel kell jönnie. De mindenki tudja, hogy ez szinte soha nem történik meg, mert a fejek és a farok gyakoriságának aránya 4-6, 9-1, 2-8 stb. Ahogy azonban az érmefeldobások száma növekszik, például 100-ra, a fejek vagy a farok megszerzésének valószínűsége eléri az 50%-ot. Ha elméletileg végtelen számú hasonló kísérletet végzünk, akkor annak a valószínűsége, hogy egy érme mindkét oldalon kiesik, mindig 50%-ra fog emelkedni.

Számos véletlenszerű tényező befolyásolja, hogy pontosan hogyan fog leesni az érme. Ez az érme helyzete a tenyerében, az erő, amellyel a dobás történik, az esés magassága, sebessége stb. De ha sok kísérlet van, függetlenül attól, hogy a tényezők hogyan befolyásolják, mindig lehet vitatkozni, hogy a gyakorlati valószínűség közel van az elméleti valószínűséghez.

Íme egy másik példa, amely segít megérteni a nagy számok törvényének lényegét: tegyük fel, hogy meg kell becsülnünk egy bizonyos régióban élő emberek kereseti szintjét. Ha 10 megfigyelést veszünk figyelembe, ahol 9 ember 20 ezer rubelt kap, 1 személy pedig 500 ezer rubelt, akkor a számtani átlag 68 ezer rubel lesz, ami természetesen nem valószínű. De ha 100 megfigyelést veszünk figyelembe, ahol 99 ember 20 ezer rubelt, 1 személy pedig 500 ezer rubelt kap, akkor a számtani átlag kiszámításakor 24,8 ezer rubelt kapunk, ami közelebb áll a dolgok valós állapotához. A megfigyelések számának növelésével arra kényszerítjük az átlagértéket, hogy a valós érték felé forduljon.

Éppen ezért a nagy számok törvényének alkalmazásához először statisztikai anyagot kell gyűjteni, hogy nagyszámú megfigyelés tanulmányozásával valódi eredményeket kapjunk. Ezért célszerű ezt a törvényt ismét a statisztikában vagy a társadalomgazdaságtanban használni.

Foglaljuk össze

A nagy számok törvényének működésének jelentőségét nehéz túlbecsülni a tudomány bármely területén, és különösen a statisztika elmélete és a statisztikai megismerés módszerei terén elért tudományos fejlemények szempontjából. A törvény hatása magukra a vizsgált tárgyakra is nagy jelentőséggel bír tömegmintázataikkal. A statisztikai megfigyelés szinte minden módszere a nagy számok törvényén és a matematikai statisztika elvén alapul.

De a tudomány és a statisztika, mint olyan figyelembevétele nélkül is nyugodtan megállapíthatjuk, hogy a nagy számok törvénye nem csupán a valószínűségszámítás területéről származó jelenség, hanem olyan jelenség, amellyel életünk során szinte minden nap találkozunk.

Reméljük, hogy most a nagy számok törvényének lényege világossá vált számodra, és könnyen és egyszerűen elmagyarázhatod másnak. És ha a matematika és a valószínűségszámítás témaköre elvileg érdekes, akkor javasoljuk, hogy olvassa el a és a. Nézze meg továbbá és. És persze figyelj a miénkre, mert annak elvégzése után nem csak új gondolkodási technikákat sajátítasz el, hanem általában kognitív képességeidet is fejleszted, beleértve a matematikaiakat is.

A véletlenszerű jelenségek vizsgálatának gyakorlata azt mutatja, hogy bár az egyedi megfigyelések eredményei, még az azonos körülmények között végzett megfigyelések eredményei is nagymértékben eltérhetnek, ugyanakkor az átlagos eredmények kellően nagy számú megfigyelés esetén stabilak és gyengén függenek a megfigyelésektől. egyéni megfigyelések eredményei.

A véletlenszerű jelenségek e figyelemre méltó tulajdonságának elméleti alapja az nagy számok törvénye. A „nagy számok törvénye” elnevezés olyan tételek csoportját egyesíti, amelyek nagyszámú véletlenszerű jelenség átlagos eredményének stabilitását állapítják meg, és megmagyarázzák ennek a stabilitásnak az okát.

A nagy számok törvényének legegyszerűbb formája és történetileg e szakasz első tétele az Bernoulli tétele, amely kimondja, hogy ha egy esemény valószínűsége minden kísérletben azonos, akkor a kísérletek számának növekedésével az esemény gyakorisága az esemény valószínűségére hajlik, és megszűnik véletlenszerű lenni.

A Poisson-tétel kimondja, hogy egy esemény gyakorisága független kísérletek sorozatában a valószínűségek számtani átlagához hajlik, és megszűnik véletlenszerű lenni.

Valószínűségszámítás határtételei, tételek Moivre-Laplace magyarázza el egy esemény előfordulási gyakoriságának stabilitásának természetét. Ez a természet abban rejlik, hogy egy esemény előfordulási számának korlátozó eloszlása ​​a kísérletek számának korlátlan növekedésével (ha az esemény valószínűsége minden kísérletben azonos) normális eloszlás.

A központi határtétel megmagyarázza a széles körben elterjedt normális törvény disztribúciók. A tétel kimondja, hogy amikor egy valószínűségi változó nagyszámú, véges varianciájú független valószínűségi változó összeadásával jön létre, ennek a valószínűségi változónak az eloszlási törvénye gyakorlatilag Normál törvény szerint.

Az alábbi tétel: " A nagy számok törvénye" kimondja, hogy bizonyos, meglehetősen általános feltételek mellett a valószínűségi változók számának növekedésével a számtani átlaguk a matematikai elvárások számtani átlagához hajlik, és megszűnik véletlenszerű lenni.

Ljapunov tétele megmagyarázza az elterjedt normális törvény eloszlását és elmagyarázza kialakulásának mechanizmusát. A tétel lehetővé teszi, hogy kijelentsük, hogy amikor egy valószínűségi változó nagyszámú független valószínűségi változó összeadásával jön létre, amelyek szórása kicsi az összeg szórásához képest, akkor ennek a valószínűségi változónak az eloszlási törvénye megfordul. hogy gyakorlatilag legyen Normál törvény szerint. És mivel a valószínűségi változókat mindig végtelen számú ok generálja, és leggyakrabban egyiknek sincs olyan szórása, mint magának a valószínűségi változónak, a gyakorlatban előforduló valószínűségi változók többségére a normál eloszlási törvény vonatkozik.

A nagy számok törvényének minőségi és mennyiségi állításai azon alapulnak Csebisev egyenlőtlenség. Meghatározza annak a valószínűségének felső korlátját, hogy egy valószínűségi változó értékének eltérése a matematikai elvárásától nagyobb, mint egy adott szám. Figyelemre méltó, hogy Csebisev egyenlőtlensége becslést ad egy esemény valószínűségére egy ismeretlen eloszlású valószínűségi változónál csak a matematikai elvárása és varianciája ismert.

Csebisev egyenlőtlensége. Ha egy x valószínűségi változónak van szórása, akkor bármely e > 0 esetén a következő egyenlőtlenség érvényesül: , Ahol M x és D x - az x valószínűségi változó matematikai elvárása és varianciája.

Bernoulli tétele. Legyen m n az n Bernoulli-próba sikereinek száma és p a siker valószínűsége egy egyéni kísérletben. Ekkor bármely e > 0 esetén igaz .

Központi határérték tétel. Ha az x 1 , x 2 , …, x n , … valószínűségi változók páronként függetlenek, azonos eloszlásúak és véges szórással rendelkeznek, akkor n ® esetén egyenletesen x-ben (- ,)