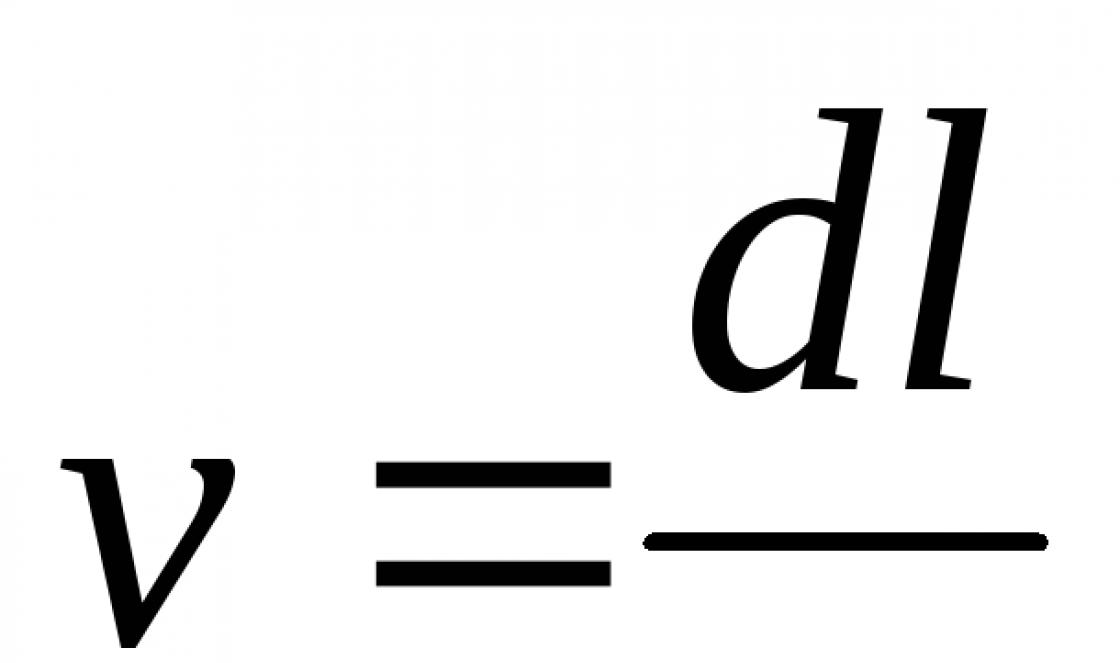WITH BELIEVABLE "FROM END TO BEGINNING" REASONS IN ASSESSING TECHNOLOGICAL PROCESS FACTORS

General information about the dimensional analysis method

When studying mechanical phenomena a number of concepts are introduced, for example, energy, speed, voltage, etc., which characterize the phenomenon under consideration and can be given and determined using a number. All questions about motion and equilibrium are formulated as problems of determining certain functions and numerical values ​​for the quantities characterizing the phenomenon, and when solving such problems in purely theoretical studies, the laws of nature and various geometric (spatial) relationships are presented in the form of functional equations - usually differential.

Very often, we do not have the opportunity to formulate the problem in a mathematical form, since the studied mechanical phenomenon is so complex that there is no acceptable scheme for it yet and there are no equations of motion yet. We encounter such a situation when solving problems in the field of aircraft mechanics, hydromechanics, in problems of studying strength and deformations, and so on. In these cases, the main role is played by experimental research methods, which make it possible to establish the simplest experimental data, which subsequently form the basis of coherent theories with a strict mathematical apparatus. However, the experiments themselves can be carried out only on the basis of a preliminary theoretical analysis. The contradiction is resolved during the iterative process of research, putting forward assumptions and hypotheses and testing them experimentally. At the same time, they are based on the presence of similarity of natural phenomena, as a general law. The theory of similarity and dimensions is to a certain extent the "grammar" of the experiment.

Dimension of quantities

Units of measurement of various physical quantities, combined on the basis of their consistency, form a system of units. Currently, the International System of Units (SI) is used. In the SI, independently of one another, the units of measurement of the so-called primary quantities are chosen - mass (kilogram, kg), length (meter, m), time (second, sec, s), current strength (ampere, a), temperature (degree Kelvin, K) and the strength of light (candle, sv). They are called basic units. The units of measurement of the remaining, secondary, quantities are expressed in terms of the main ones. The formula that indicates the dependence of the unit of measurement of a secondary quantity on the main units of measurement is called the dimension of this quantity.

The dimension of a secondary quantity is found using the defining equation, which serves as the definition of this quantity in mathematical form. For example, the defining equation for speed is

.

We will indicate the dimension of a quantity using the symbol of this quantity taken in square brackets, then

, or
,

where [L], [T] are the dimensions of length and time, respectively.

The defining equation for force can be considered Newton's second law

Then the dimension of the force will have the following form

[F]=[M][L][T] .

The defining equation and the formula for the dimension of work, respectively, will have the form

A=Fs and [A]=[M][L] [T] .

In the general case, we will have the relationship

[Q] =[M] [L] [T] (1).

Let's pay attention to the record of the relationship of dimensions, it will still be useful to us.

Similarity theorems

The formation of the theory of similarity in the historical aspect is characterized by its three main theorems.

First similarity theorem formulates the necessary conditions and properties of such systems, arguing that such phenomena have the same similarity criteria in the form of dimensionless expressions, which are a measure of the ratio of the intensity of two physical effects that are essential for the process under study.

Second similarity theorem(P-theorem) proves the possibility of reducing the equation to a criterion form without determining the sufficiency of conditions for the existence of similarity.

Third similarity theorem points to the limits of the regular distribution of a single experience, because similar phenomena will be those that have similar conditions for uniqueness and the same defining criteria.

Thus, the methodological essence of the theory of dimensions lies in the fact that any system of equations that contains a mathematical record of the laws governing the phenomenon can be formulated as a relationship between dimensionless quantities. The determining criteria are composed of mutually independent quantities that are included in the uniqueness conditions: geometric relationships, physical parameters, boundary (initial and boundary) conditions. The system of defining parameters must have the properties of completeness. Some of the defining parameters can be physical dimensional constants, we will call them fundamental variables, in contrast to others - controlled variables. An example is the acceleration of gravity. She is a fundamental variable. Under terrestrial conditions - a constant value and - a variable in space conditions.

For the correct application of dimensional analysis, the researcher must know the nature and number of fundamental and controlled variables in his experiment.

In this case, there is a practical conclusion from the theory of dimensional analysis and it lies in the fact that if the experimenter really knows all the variables of the process under study, and there is still no mathematical record of the law in the form of an equation, then he has the right to transform them by applying the first part Buckingham's theorems: "If any equation is unambiguous with respect to dimensions, then it can be converted to a relation containing a set of dimensionless combinations of quantities."

Homogeneous with respect to dimensions is an equation whose form does not depend on the choice of basic units.

PS. Empirical patterns are usually approximate. These are descriptions in the form of inhomogeneous equations. In their design, they have dimensional coefficients that "work" only in a certain system of units of measurement. Subsequently, with the accumulation of data, we come to a description in the form of homogeneous equations, i.e., independent of the system of units of measurement.

Dimensionless combinations, in question, are products or ratios of quantities, drawn up in such a way that in each combination of dimensions are reduced. In this case, the products of several dimensional quantities of different physical nature form complexes, the ratio of two dimensional quantities of the same physical nature - simplices.

Instead of varying each of the variables in turn,and changing some of them can causedifficulties, the researcher can only varycombinations. This circumstance greatly simplifies the experiment and makes it possible to present in graphical form and analyze the obtained data much faster and with greater accuracy.

Using the method of dimensional analysis, organizing plausible reasoning "from the end to the beginning".

After reviewing the above general information, you can especially pay attention to the following points.

The most efficient use of dimensional analysis is in the presence of one dimensionless combination. In this case, it is sufficient to experimentally determine only the matching coefficient (it is enough to set up one experiment to compile and solve one equation). The task becomes more complicated with an increase in the number of dimensionless combinations. Compliance with the requirement of a complete description of the physical system, as a rule, is possible (or perhaps they think so) with an increase in the number of variables taken into account. But at the same time, the probability of complication of the form of the function increases and, most importantly, the amount of experimental work increases sharply. The introduction of additional basic units somehow relieves the problem, but not always and not completely. The fact that the theory of dimensional analysis develops over time is very encouraging and orients to the search for new possibilities.

Well, what if, when searching for and forming a set of factors to be taken into account, i.e., in fact, recreating the structure of the physical system under study, we use the organization of plausible reasoning "from end to beginning" according to Pappus?

In order to comprehend the above proposal and consolidate the foundations of the dimensional analysis method, we propose to analyze an example of establishing the relationship of factors that determine the efficiency of explosive breaking during underground mining of ore deposits.

Taking into account the principles of the systems approach, we can rightfully judge that two systemic interacting objects form a new dynamic system. In production activities, these objects are the object of transformation and the subject instrument of transformation.

When breaking ore on the basis of explosive destruction, we can consider the ore massif and the system of explosive charges (wells) as such.

When using the principles of dimensional analysis with the organization of plausible reasoning "from end to beginning", we obtain the following line of reasoning and a system of interrelations between the parameters of the explosive complex and the characteristics of the array.

d m = f 1 (W ,I 0 ,t deputy , s)	d m = k 1 W(st deputy ¤ I 0 W) n (1)
I 0 = f 2 (I c ,V Boer ,K And )	I 0 = k 2 I c V Boer K And (2)
I c = f 3 (t deputy ,Q ,A)	I With = k 3 t air 2/3 Q 2/3 A 1/3 (3)
t air = f 4 (r zab ,P Max l well )	t air = k 4 r zab 1/2 P Max –1/2 l well (4)
P Max = f 5 (r zar D)	P Max = k 5 r zar D 2 (5)

The designations and formulas for the dimensions of the variables used are given in the Table.

VARIABLES	Designation	dimensions
Maximum crushing diameter	d m	[ L]
Line of least resistance		[ L]
Compressive strength of rocks
Period (interval) of deceleration of blasting	t deputy	[ T]
Explosion impulse per 1 m 3 of the array	I 0
Specific consumption of drilling, m / m 3	V Boer	[ L -2 ]
The utilization rate of wells under charge	TO is
Explosion impulse per 1 m of well	I c
Explosion energy per 1 m of charge
Acoustic hardness of the medium (A=gC)
The impact time of the explosion in the well	t air	[ T]
stemming density	r zab	[ L -3 M]
Well length	l well	[ L]
Maximum initial well pressure		[ L -1 M T -2 ]
Charge density in the well	r zar	[ L -3 M]
Explosive detonation speed		[ L T -1 ]

Passing from formula (5) to formula (1), revealing the established relationships, and also keeping in mind the previously established relationship between the diameter of the average and the diameter of the maximum piece in terms of collapse

d Wed = k 6 d m 2/3 , (6)

we obtain the general equation for the relationship of factors that determine the quality of crushing:

d Wed = kW 2/3 [ s t deputy / r zab 1/3 D -2/3 l well 2/3 M zar 2|3 U centuries 2/3 A 1/3 V Boer TO is W] n (7)

Let us transform the last expression in order to create dimensionless complexes, while keeping in mind:

Q= M zar U centuries ; q centuries =M zar V Boer TO is ; M zab =0.25 p r zab d well 2 ;

Where M zar is the mass of the explosive charge in 1 m of the well length, kg/m;

M zab – mass of stemming in 1 m of stemming, kg/m;

U centuries – calorific value of explosives, kcal/kg.

In the numerator and denominator we use [M zar 1/3 U centuries 1/3 (0.25 pd well 2 ) 1/3 ] . We will finally get

All complexes and simplices have a physical meaning. According to experimental data and practice data, the power exponent n=1/3, and coefficient k is determined depending on the scale of simplification of expression (8).

Although the success of dimensional analysis depends on a correct understanding of the physical meaning of a particular problem, after the choice of variables and basic dimensions, this method can be applied completely automatically. Therefore, this method can be easily stated in prescription form, bearing in mind, however, that such a "recipe" requires the researcher to correctly select the constituent components. The only thing we can do here is to give some general advice.

Stage 1. Select independent variables that affect the system. Dimensional coefficients and physical constants should also be considered if they play an important role. This is the most responsibleny stage of the whole work.

Stage 2. Choose a system of basic dimensions through which you can express the units of all selected variables. The following systems are commonly used: in mechanics and fluid dynamics MLq(Sometimes FLq), V thermodynamics MLqT or MLqTH; in electrical engineering and nuclear physics MLqTO or MLqm., in this case, the temperature can either be considered as a basic quantity, or expressed in terms of molecular kinetic energy.

Stage 3. Write down the dimensions of the selected independent variables and make dimensionless combinations. The solution will be correct if: 1) each combination is dimensionless; 2) the number of combinations is not less than that predicted by the p-theorem; 3) each variable occurs in combinations at least once.

Stage 4. Examine the resulting combinations in terms of their acceptability, physical meaning and (if least squares method is to be used) concentration of uncertainty in one combination if possible. If the combinations do not meet these criteria, then one can: 1) get another solution to the equations for the exponents in order to find the best set of combinations; 2) choose another system of basic dimensions and do all the work from the very beginning; 3) check the correctness of the choice of independent variables.

Stage 5. When a satisfactory set of dimensionless combinations is obtained, the researcher can plan to change the combinations by varying the values ​​of the selected variables in his equipment. The design of experiments should be given special consideration.

When using the method of dimensional analysis with the organization of plausible reasoning "from the end to the beginning", it is necessary to introduce serious corrections, and especially at the first stage.

Brief conclusions

Today it is possible to form the conceptual provisions of research work according to the already established normative algorithm. Step-by-step following allows you to streamline the search for a topic and determine its stages of implementation with access to scientific provisions and recommendations. Knowledge of the content of individual procedures contributes to their expert evaluation and selection of the most appropriate and effective.

Progress of scientific research can be presented in the form of a logical scheme, determined in the process of performing research, highlighting three stages that are characteristic of any activity:

Preparatory stage: It can also be called the stage of methodological preparation of research and the formation of methodological support for research. The scope of work is as follows. Definition of the problem, development of a conceptual description of the subject of research and definition (formulation) of the research topic. Drawing up a research program with the formulation of tasks and the development of a plan for their solution. Reasonable choice of research methods. Development of a methodology for experimental work.

Main stage: - executive (technological), implementation of the program and research plan.

final stage: - processing of research results, formulation of the main provisions, recommendations, expertise.

Scientific provisions are a new scientific truth - this is what needs and can be defended. The formulation of scientific provisions can be mathematical or logical. Scientific provisions help the cause, the solution of the problem. Scientific provisions should be targeted, i.e. reflect (contain) the topic for which they were solved. In order to carry out a general linkage of the content of R&D with the strategy for its implementation, it is recommended to work on the structure of the R&D report before and (or) after the development of these provisions. In the first case, work on the structure of the report even has heuristic potential, contributes to the understanding of R&D ideas, in the second case, it acts as a kind of strategy test and feedback for R&D management.

Let's remember that there is a logic of searching, doing work and lo geek presentation. The first is dialectical - dynamic, with cycles, returns, difficult to formalize, the second is the logic of a static state, formal, i.e. having a strictly defined form.

As a conclusion it is desirable not to stop working on the structure of the report during the entire time of the research and thus episodically "check the clocks of TWO LOGICS".

The systematization of modern problems of mining at the administrative level contributes to the increase in the efficiency of work on the concept.

In the methodological support of research work, we often encounter situations where the theoretical provisions on a specific problem have not yet been fully developed. It is appropriate to use methodological "leasing". As an example of such an approach and its possible use, the method of dimensional analysis with the organization of plausible reasoning "from end to beginning" is of interest.

Basic terms and concepts

Object and subject of activity	Relevance	mining technology
Concept		Mining technology facility
Purpose and goal setting		Mining Technology Tools
problem problem situation	Structure	Physical and technical effect
Stages and stages of research		Scientific position
Similarity theorems	Dimension	Basic units

Experience is the explorer of nature. He never deceives... We must make experiments by changing the circumstances until we extract general rules from them, because experience provides true rules.

Leonardo da Vinci

Physical quantities, the numerical value of which does not depend on the chosen scale of units, are called dimensionless. Examples of dimensionless quantities are the angle (the ratio of the arc length to the radius), the refractive index of matter (the ratio of the speed of light in vacuum to the speed of light in matter).

Physical quantities that change their numerical value when the scale of units is changed are called dimensional. Examples of dimensional quantities are length, force, etc. The expression of a unit of a physical quantity in terms of basic units is called its dimension (or dimension formula). For example, the dimension of force in the CGS and SI systems is expressed by the formula

Considerations of dimension can be used to check the correctness of the answers obtained when solving physical problems: the right and left parts of the obtained expressions, as well as individual terms in each of the parts, must have the same dimension.

The method of dimensions can also be used to derive formulas and equations, when we know on what physical parameters the desired value may depend. The essence of the method is easiest to understand with specific examples.

Applications of the method of dimensions. Consider a problem for which the answer is well known to us: with what speed will a body fall to the ground, freely falling without an initial velocity from a height, if air resistance can be neglected? Instead of a direct calculation based on the laws of motion, we will argue as follows.

Let's think about what the desired speed may depend on. It is obvious that it must depend on the initial height and on the acceleration of free fall It can be assumed, following Aristotle, that it also depends on the mass. Since only values ​​of the same dimension can be added, the following formula can be proposed for the desired speed:

where C is some dimensionless constant (numerical coefficient), and x, y and z are unknown numbers to be determined.

The dimensions of the right and left parts of this equality must be the same, and it is this condition that can be used to determine the exponents x, y, z in (2). The dimension of speed is the dimension of height is the dimension of the acceleration of free fall is, finally, the dimension of the mass is equal to M. Since the constant C is dimensionless, formula (2) corresponds to the following equality of dimensions:

This equality must hold regardless of what the numeric values ​​are. Therefore, it is necessary to equate the exponents at and M in the left and right parts of equality (3):

From this system of equations, we obtain Therefore, formula (2) takes the form

The true value of the speed, as is known, is equal to

So, the approach used made it possible to determine correctly the dependence on and and did not make it possible to find the value

dimensionless constant C. Although we have not been able to obtain an exhaustive answer, nevertheless, very significant information has been obtained. For example, we can state with complete certainty that if the initial height is quadrupled, the speed at the moment of falling will double and that, contrary to Aristotle's opinion, this speed does not depend on the mass of the falling body.

Choice of options. When using the method of dimensions, one should first of all identify the parameters that determine the phenomenon under consideration. This is easy to do if the physical laws describing it are known. In a number of cases, the parameters determining the phenomenon can be specified even when the physical laws are unknown. As a rule, you need to know less to use the dimensional analysis method than to write equations of motion.

If the number of parameters that determine the phenomenon under study is greater than the number of basic units on which the chosen system of units is built, then, of course, all the exponents in the proposed formula for the desired value cannot be determined. In this case, it is useful first of all to determine all independent dimensionless combinations of the chosen parameters. Then the desired physical quantity will be determined not by a formula like (2), but by the product of some (the simplest) combination of parameters that has the desired dimension (i.e., the dimension of the desired quantity) by some function of the found dimensionless parameters.

It is easy to see that in the above example of a body falling from a height, it is impossible to form a dimensionless combination from the quantities and the dimensionless combination. Therefore, formula (2) there exhausts all possible cases.

Dimensionless parameter. Let us now consider the following problem: we determine the range of the horizontal flight of a projectile fired in a horizontal direction with an initial velocity from a gun located on a mountain of height

In the absence of air resistance, the number of parameters on which the desired range may depend is equal to four: and m. Since the number of basic units is equal to three, a complete solution of the problem by the method of dimensions is impossible. Let us first find all the independent dimensionless parameters y that can be composed of and

This expression corresponds to the following equality of dimensions:

From here we get the system of equations

which gives and for the desired dimensionless parameter we obtain

It can be seen that the only independent dimensionless parameter in the problem under consideration is .

where is the yet unknown function of the dimensionless parameter. The method of dimensions (in the presented version) does not allow one to determine this function. But if we know from somewhere, for example, from experience, that the desired range is proportional to the horizontal velocity of the projectile, then the form of the function is immediately determined: the velocity must enter into it to the first power, i.e.

Now from (5) for the range of the projectile we get

which matches the correct answer

We emphasize that with this method of determining the type of function, it is enough for us to know the nature of the experimentally established dependence of the flight range not on all parameters, but only on one of them.

Vector units of length. But it is possible to determine the range (7) only from dimensional considerations, if we increase to four the number of basic units in terms of which the parameters are expressed, etc. Until now, when writing dimensional formulas, no distinction was made between units of length in the horizontal and vertical directions. However, such a distinction can be introduced based on the fact that gravity acts only vertically.

Let us denote the dimension of length in the horizontal direction through and in the vertical direction - through Then the dimension of the flight range in the horizontal direction will be the dimension of height will be the dimension of the horizontal speed will be and for acceleration

free fall we get Now, looking at formula (5), we see that the only way to get the right dimension on the right side is to consider it proportional. We again come to formula (7).

Of course, having four basic units and M, one can directly construct the value of the required dimension from four parameters and

The equality of the dimensions of the left and right parts has the form

The system of equations for x, y, z and and gives the values ​​and we again come to formula (7).

The different units of length used here in mutually perpendicular directions are sometimes referred to as vector units of length. Their application significantly expands the possibilities of the dimensional analysis method.

When using the dimensional analysis method, it is useful to develop skills to such an extent that you do not make a system of equations for the exponents in the desired formula, but select them directly. Let's illustrate this in the next problem.

Task

Maximum range. At what angle to the horizontal should a stone be thrown to maximize the horizontal flight range?

Solution. Let's assume that we have "forgotten" all kinematics formulas and try to get an answer from dimensional considerations. At first glance, it may seem that the method of dimensions is not applicable here at all, since some trigonometric function of the throwing angle must enter into the answer. Therefore, instead of the angle a itself, we will try to look for an expression for the range. It is clear that we cannot do without vector units of length.

In cases where there are no equations describing the process, and it is not possible to create them, it is possible to use the analysis of dimensions to determine the type of criteria from which the similarity equation should be compiled. Beforehand, however, it is necessary to determine all the parameters essential for the description of the process. This can be done on the basis of experience or theoretical considerations.

The method of dimensions subdivides physical quantities into basic (primary), which characterize the measure directly (without connection with other quantities), and derivatives, which are expressed through the basic quantities in accordance with physical laws.

In the SI system, the basic units are assigned designations: length L, weight M, time T, temperature Θ , current strength I, the power of light J, amount of substance N.

Derived value expression φ through the main is called the dimension. The formula for the dimension of a derived quantity, for example, with four basic units of measurement L, M, T, Θ, looks like:

Where a, b, c, d are real numbers.

In accordance with the equation, dimensionless numbers have zero dimension, and basic quantities have dimension equal to one.

In addition to the above principle, the method is based on the axiom that only quantities and complexes of quantities that have the same dimension can be added and subtracted. From these provisions it follows that if any physical quantity, for example ∆ p, is defined as a function of other physical quantities in the form ∆ p= f(V, ρ, η, l, d) , then this dependence can be represented as:

,

Where C- constant.

If we then express the dimension of each derived quantity in terms of the main dimensions, then we can find the values ​​of the exponents x, y, z etc. Thus:

In accordance with the equation, after substituting the dimensions, we obtain:

Grouping then homogeneous terms, we find:

If in both parts of the equation we equate the exponents with the same basic units, we get the following system of equations:

There are five unknowns in this system of three equations. Therefore, any three of these unknowns can be expressed in terms of the other two, namely x, y And r through z And v:

After substituting the exponents
And into a power function it turns out:

.

The criterion equation describes the fluid flow in the pipe. This equation includes, as shown above, two criteria-complexes and one criterion-simplex. Now, using the analysis of dimensions, the types of these criteria are established: this is the Euler criterion Eu=∆ p/(ρ V 2 ) , Reynolds criterion Re= Vdρ/η and parametric criterion of geometric similarity G=l/ d. In order to finally establish the form of the criterion equation, it is necessary to experimentally determine the values ​​of the constants C, z And v in the equation.

1. Experimental determination of the constants of the criterion equation

When conducting experiments, the dimensional quantities contained in all similarity criteria are measured and determined. According to the results of the experiments, the values ​​of the criteria are calculated. Then they make up tables, in which, according to the values ​​of the criterion K 1 enter the values ​​of the defining criteria K 2 , K 3 etc. This operation completes the preparatory stage of processing experiments.

To generalize tabular data as a power law:

logarithmic coordinate system is used. The selection of exponents m, n etc. achieve such an arrangement of experimental points on the graph so that a straight line can be drawn through them. The straight line equation gives the desired relationship between the criteria.

Let us show how to determine in practice the constants of the criterion equation:

.

In logarithmic coordinates lgK 2 – lgK 1 this is the straight line equation:

.

Putting the experimental points on the graph (Fig. 4), draw a straight line through them, the slope of which determines the value of the constant m= tgβ.

Rice. 4. Processing of experimental data

It remains to find a constant . For any point on a straight line on the graph
. Therefore, the value C find by any pair of corresponding values K 1 And K 2 counted on the straight line of the graph. For the reliability of the value determined by several points of a straight line and the average value is substituted into the final formula:

With a larger number of criteria, the determination of the equation constants becomes somewhat more complicated and is carried out according to the method described in the book.

In logarithmic coordinates, it is not always possible to arrange experimental points along a straight line. This happens when the observed dependence is not described by a power equation and it is necessary to look for a function of a different type.

Many of the processes encountered in practice are so complex that they cannot be directly described by differential equations. In such cases, a very valuable technique for revealing the relationship between variables is the analysis of dimensions.

This method does not provide complete information about the relationship between variables, which, ultimately, must be revealed experimentally. However, this method can significantly reduce the amount of experimental work.

Thus, the effective application of the dimensional method is possible only when combined with experiment; in this case, all factors or variables that affect the process under study must be known.

Dimensional analysis gives a logical distribution of quantities over dimensionless groups. In general, the functional dependence of N can be represented as a formula, which is called the dimension formula:

This includes (k + 1) inclusion quantities and N quantities. They can be variable, constant, dimensional, and dimensionless. However, in this case, it is necessary that for the numerical quantities included in the equation that characterizes the physical phenomenon, the same system of basic units of measurement would be adopted. Under this condition, the equation remains valid for an arbitrarily chosen system of units. Further, these basic units should be independent in their dimensions, and their number should be such that it would be possible to represent through them the dimensions of all quantities included in the functional dependence (3.73).

Such units of measurement can be any three quantities included in equation (3.73) and which are independent of each other in terms of dimension. If we take, for example, the length L and the speed V as units of measurement, then we have the given unit of length L and the unit of time . Thus, for the third unit of measure, it is impossible to accept any quantity whose dimension contains only length and time, such as, for example, acceleration, since the unit of this quantity is already set as a result of choosing the units of length and speed. Therefore, in addition, any value must be chosen, the dimension of which includes mass, for example, density, viscosity, force, etc.

In practice, for example, in hydraulic studies, it turns out to be appropriate to take the following three units of measurement: the speed V 0 of any flow particle, any length (pipeline diameter D or its length L), density ρ of the selected particle.

The dimension of these units of measurement:

m/s; m; kg / m 3.

Thus, the equation for dimensions in accordance with the functional dependence (3.73) can be represented in the following form:

The values ​​N i and n i taken in the system of basic units (meter, second, kilogram) can be expressed in dimensionless numbers:

; .

Therefore, instead of equation (3.73), one can write an equation in which all quantities are expressed in relative units (with respect to V 0 , L 0 , ρ 0):

Since p 1, p 2, p 3 are, respectively, V 0, L 0, ρ 0, then the first three terms of the equation turn into three units and the functional dependence takes the form:

. (3.76)

In accordance with the π-theorem, any relationship between dimensional quantities can be formulated as a relationship between dimensionless quantities. In research, this theorem makes it possible to determine the relationship not between the variables themselves, but between some of their dimensionless ratios, compiled according to certain laws.

Thus, the functional dependence between k + 1 dimensional quantities N and n i is generally expressed as the ratio between (k + 1- 3) quantities π and π i (i = 4.5, ..., k), each of which is a dimensionless power combination of the quantities included in the functional dependence. Dimensionless numbers π have the character of similarity criteria, as can be seen from the following example.

Example 3.3. Determine the functional dependence for the resistance force F (N = kg m / s 2), which the plate experiences when flowing around with liquid in the direction of its length.

The functional dependence of the resistance force can be represented as a function of a number of independent variables and determined under similarity conditions:

,

Where flow velocity, m/s; plate area, m 2 ; liquid density, kg/m 3 ; dynamic coefficient of viscosity, Pa s ([Pa s] = kg/m s); free fall acceleration, m/s 2 ; pressure, Pa (Pa = kg/m s); the ratio of the height of the plate to its length; the angle of inclination of the plate to the direction of flow.

Thus, the quantities and are dimensionless, the remaining six are dimensional. Three of them: , and taken as the main ones. In accordance with the π-theorem, only three dimensionless relations are possible here. Hence:

for the resistance force:

1 \u003d z (indicators on the left and right at kg);

2 \u003d - x (indicators on the left and right at c);

1 \u003d x + 2y - 3z (indicators on the left and right at m).

The solution of these equations gives: x = 2; y = 1; z = 1.

Functional dependency:

Similarly, we get:

For viscosity:

we have x 1 = 1; y 1 = 0.5; z1 = 1.

Functional dependency:

;

we have x 2 = 2; y 2 = - 0.5; z2 = 0.

Functional dependency:

For pressure:

we have x 3 = 2; y 3 = 0; z3 = 1.

Functional dependency:

.

It's obvious that , ,

.

From this we can conclude that after studying this process at certain sizes, speeds, etc., it is possible to establish how it will proceed at other sizes and speeds if the dimensionless ratios composed of these variables are the same for both cases . So, the conclusions obtained in experiments with bodies of given sizes, moving at a given speed, etc., will obviously be valid for any other body sizes, speeds, etc. provided that the dimensionless ratios are equal with those observed in experiments.

Example 3.4. Based on previous studies on a laboratory device, determine the functional dependence of the power N (W = kg m 2 /s 3) of the stirrer motor, which is necessary for mixing the pulp with reagents in the contact tank.

For the similarity of two mixing systems, it is required:

Geometric similarity, in which the ratio of quantities for the systems under consideration must be equal to each other;

Kinematic similarity, when the speeds at the corresponding points should be in the same ratio as the speeds at other corresponding points, that is, the paths of the pulp must be similar;

Dynamic similarity, which requires that the ratio of forces at corresponding points be equal to the ratio of forces at other relevant points.

If the boundary conditions are fixed, one variable can be expressed in terms of other variables, that is, the functional dependence of the power of the stirrer motor can be represented as a function of a number of independent variables and determined by similarity criteria:

,

where is the mixer diameter, m; pulp density, kg/m 3 ; stirrer rotation speed, s -1 ; dynamic coefficient of viscosity, Pa·s (Pa·s=kg/m·s); free fall acceleration, m/s 2 – the angle of inclination of the plate to the flow direction.

Thus, we have five dimensional quantities, three of them: , and taken as basic. In accordance with the π-theorem, only two dimensionless relations are possible here. Hence:

.

Given the equality of dimensions for the numerator and denominator, we find the exponents:

for the power of the stirrer motor:

,

3 \u003d z (indicators on the left and right at c);

1 = in (indicators on the left and right at kg);

2 \u003d x - 3y (indicators on the left and right at m).

The solution of these equations gives: x = 5; y = 1; z = 3.

Functional dependency:

Similarly, we get:

For viscosity:

we have x 1 = 2; y 1 = 1; z1 = 1.

Functional dependency:

;

To accelerate free fall:

we have x 2 = 1; y 2 = 0; z2 = 1.

Functional dependency:

;

It's obvious that , . Then the desired functional dependence has the form:

.

From this we can conclude that after finding the functional dependence of the power of the agitator motor for some of its parameters, it is possible to establish what it will be for other sizes and speeds, etc. if the dimensionless ratios for both cases are the same. So, the conclusions obtained on the experimental device will be valid for any other device, provided that the dimensionless ratios are equal to those observed in the experiments.

Example 3.5. The enrichment process in a heavy medium separator is investigated. The parametric diagram of the heavy media separation process (Fig. 3.5) shows the incoming, outgoing and controlled parameters, as well as possible obstacles:

Input and controlled parameters: Qin - performance of the separator for the source material; Q susp - the flow rate of the suspension; V - bucket volume; Δρ is the difference in the densities of the suspension and the fraction to be separated; ω - speed of rotation of the elevator wheel; n is the number of buckets of the elevator wheel;

Output and controlled parameters: Q to-t - performance of the separator for concentrate; Q otx - performance of the separator for waste;

Obstacles (unaccounted for parameters that affect the process): humidity, granulometric and fractional composition.

We check whether the number of parameters is sufficient for calculating the model, for which we write down the dimensions of all quantities = kg / s; \u003d m 3 / s; [Δ] \u003d kg / m 3; [V] \u003d m 3; [ ] = c -1 ; = kg/s; [n] = 8.

The main dimensional quantities m = 3 (kg, m, s), therefore, the following can be used in calculations:

parameter, i.e. Q out, V, Δ, ω.

0 = 3x - 3z (exponents on the left and right at L);

1 \u003d - y - 3z (indicators on the left and right at T);

So x = 1; y = - 2; z = 1, that is, the functional dependence of the waste separator capacity on the bucket volume, the rotation speed of the elevator wheel and the difference in the density of the suspension and the separated fraction has the form:

The value of the coefficient k is determined on the basis of previous studies with fixed parameters: V = 0.25 m 3 ; Δ \u003d 100 kg / m 3; = 0.035 s -1; n \u003d 8, as a result of which it was found that Q otx \u003d 42 kg / s:

Formula is a mathematical model of the process under study.

Example 3.6. The process of transporting a concentrate with a particle size of 0.5 - 13 mm by a dewatering bagger-sump elevator is being studied:

Input and controlled parameters: ω - capacity of the elevator bucket in terms of solids; ρ - supply density; V is the speed of the elevator chain;

Output and controlled parameter: Q - productivity of the dewatering bagger-sump elevator according to the class 0.5 - 13 mm;

Constant parameters: bucket fill factor = 0.5; humidity, granulometric and fractional composition.

In this example:

We check whether the number of parameters is sufficient for calculating the model, for which we write down the dimensions of all quantities: [ω] = m 3; [ρ] \u003d kg / m 3; [V] = m/s.

The main dimensional quantities m = 3 (kg, m, s), therefore, the following can be used in calculations:

parameter, i.e. Q, V, , ω.

Since not all parameters are taken into account, the coefficient k is added to the functional dependence between the selected parameters:

,

or using base units M, L, T:

0 \u003d 3x + y - 3z (indicators on the left and right at L);

1 \u003d - y (indicators on the left and right at T);

1 = z (exponents on the left and right at M).

So x = 2/3; y = 1; z = 1, that is, the functional dependence of the productivity of the dewatering bagger-sump elevator according to the class 0.5-13 mm on the bucket volume, the speed of the elevator chain and the feed density has the form:

.

The value of the coefficient k is determined on the basis of previous studies with fixed parameters: V = 0.25 m/s; \u003d 1400 kg / m 3; \u003d 50 10 -3 m 3 as a result of which it was found that Q \u003d 1.5 kg / s, in addition, the filling factor of the buckets should be taken into account = 0.5 and then:

.

Formula is a mathematical model of the process of transporting a concentrate with a particle size of 0.5-13 mm by the investigated dewatering bagger-sump elevator.

It should be borne in mind that the smaller the value of the coefficient k, the greater the value of the parameters under consideration.

The dimensional analysis method is often very effective in solving complex problems of mechanics, in particular, in hydraulics, fluid dynamics and aerodynamics. Together with the idea of ​​the physical meaning of phenomena or with the involvement of experimental data, it leads, and, moreover, quickly and simply, to results evaluating a given phenomenon.

In the domestic literature, the methods of similarity and dimension are described in a monograph, for example [Sena]; [Sedova]; [Kogan]. Recognizing that the π-theorem is fundamental, we mention and explain it once; in the future, in terms of level and generality, we adhere to the book [Kogan].

Basic definitions.

There are several systems of units of measurement (CGS, SI, etc.) and in each of them some physical quantities are conventionally taken as main or primary, i.e. those for which the units are set arbitrarily and independently. In mechanics, and in particular in hydromechanics and hydraulics, a system is used L , m , t , in which the length is taken as the main quantities L, weight m and time t. Obviously, when analyzing any phenomenon, the units of mass, time, and length are chosen independently of each other. To secondary quantities include those that are obtained as combinations of the main ones. For example, secondary quantities include: speed V= S/ t or [ V]= Lt -1 , acceleration a= V/ t or [ a]= Lt -2 , density ρ= m/ W or [ ρ ]= mL -3 and many other quantities. The square brackets in which the designation of the quantity is placed means that we are talking about the dimension of the unit of this quantity, and the symbols L,m,t are generalized designations for units of length, mass and time without specifying the specific name of the units.

In special courses it is shown that the formula for the dimension of secondary quantities should be power-law with respect to all basic physical quantities. Suppose, for example, that the number of basic quantities is chosen to be three and the length is taken as them L, weight m and time t. Then the dimension of the physical quantity y represented by the formula

[y]= L α m β t γ , (.1)

Where α , β , γ are constant numbers (recall that the square brackets in which the symbol of magnitude is placed y, means that the dimension of this quantity is considered). Formula (.1) is called the formula for the dimension of the unit of a given quantity or, as is often said, briefly dimension of this quantity.

It must be emphasized that you can multiply and divide physical quantitiesanydimensions, and only values ​​of the same dimension can be added and subtracted.

Example(.1) . Speed V can be expressed as V= L/ t= L 1 m 0 t -1 , i.e. α =1 , β =0, γ =-1 .Force F= ma can be presented as F= mL/ t²= L 1 m 1 t -2 , i.e. α =1 , β =1 , γ = -2 .

Not necessary α , β , γ are rational numbers, but there is no need to enter numbers other than rational ones. Often the dimension of a physical quantity is identified with its unit in the corresponding system of units. So, for example, they say that speed has the dimension cm/s (centimeter per second). Although this is not logical, but there is no gross error in this. In this case cm/s is Name units (just like km / h, m / s, etc.). Always, if necessary, units of this type allow you to go to dimensional formulas in which the scales of the units of basic quantities are not fixed.

Remark 1. Different physical quantities can have the same dimensions even in the same system of units. Examples in mechanics are work and kinetic energy or work and moment of force (system Lmt).

Remark 2. Dimensionless combinations of physical quantities are such combinations that have zero dimension in the considered system of units. Their numerical values ​​do not change when the scales of the units of the basic quantities change.

Task 1. Find dimensions: 1) pressure; 2) energy; 3) coefficient of dynamic viscosity; 4) coefficient of kinematic viscosity; 5) coefficient of surface tension.

All results that can be obtained using the dimensional analysis method are based on two theorems.