Addition and subtraction of decimal fractions.
Multiplying decimals.
Division of decimals.
Addition and subtraction of decimal fractions. These operations are performed in the same way as addition and subtraction of integers. It is only necessary to write the corresponding decimal places one under the other.
EXAMPLE
Multiplying decimals. In the first step, we multiply the decimal fractions as whole numbers, without taking into account the decimal point. The following rule is then applied: the number of decimal places in the product is equal to the sum of the decimal places in all factors.
Comment: before decimal point V work cannot bediscard trailing zeros !
EXAMPLE
The sum of the numbers of decimal places in the factors is: 3 + 4 = 7. The sum of the digits in the product is 6. Therefore, you need to add one zero to the left: 0197056 and put a decimal point in front of it: 0.0197056.
Decimal division
Divide a decimal by an integer
If dividend is less than divisor, we write zero in the integer part of the quotient and put a decimal point after it. Then, not taking into account the decimal point of the dividend, we add the next digit of the fractional part to its integer part and again compare the resulting integer part of the dividend with the divisor. If the new number is again less than the divisor, put one more zero after the decimal point in the quotient and add the next digit of its fractional part to the integer part of the dividend. This process is repeated until the resulting dividend becomes more divisor. After that division is performed as for integers. If dividend is greater than or equal to the divisor, first we divide its integer part, write the result of division in private and put a decimal point. After that, the division continues, as in the case of integers.
EXAMPLE Divide 1.328 by 64.
Solution: 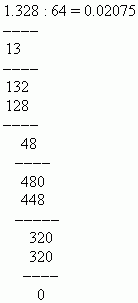
Division of one decimal fraction by another.
First, we transfer the decimal points in the dividend and the divisor by the number of decimal places in the divisor, that is, we make the divisor an integer. Now we perform the division, as in the previous case.
EXAMPLE Divide 0.04569 by 0.0006.
Solution.
We transfer decimal points for 4 positions to the right And divide 456.9 on 6:Actions with fractions. In this article, we will analyze examples, everything is detailed with explanations. We will consider ordinary fractions. In the future, we will analyze decimals. I recommend to watch the whole and study sequentially.
1. Sum of fractions, difference of fractions.
Rule: when adding fractions with equal denominators, the result is a fraction - the denominator of which remains the same, and its numerator will be equal to the sum of the numerators of the fractions.
Rule: when calculating the difference of fractions with the same denominators, we get a fraction - the denominator remains the same, and the numerator of the second is subtracted from the numerator of the first fraction.
Formal notation of the sum and difference of fractions with equal denominators:

Examples (1):

It is clear that when ordinary fractions are given, then everything is simple, but if they are mixed? Nothing complicated...
Option 1- you can convert them into ordinary ones and then calculate them.
Option 2- you can separately "work" with the integer and fractional parts.
Examples (2):

More:
And if the difference of two mixed fractions and the numerator of the first fraction will be less than the numerator of the second? It can also be done in two ways.
Examples (3):
* Translated into ordinary fractions, calculated the difference, converted the resulting improper fraction into a mixed one.

* Divided into integer and fractional parts, got three, then presented 3 as the sum of 2 and 1, with the unit presented as 11/11, then found the difference between 11/11 and 7/11 and calculated the result. The meaning of the above transformations is to take (select) the unit and present it as a fraction with the denominator we need, then from this fraction we can already subtract another.
Another example:

Conclusion: there is a universal approach - in order to calculate the sum (difference) of mixed fractions with equal denominators, they can always be converted into improper ones, then perform the necessary action. After that, if as a result we get an improper fraction, we translate it into a mixed one.
Above, we looked at examples with fractions that have equal denominators. What if the denominators differ? In this case, the fractions are reduced to the same denominator and the specified action is performed. To change (transform) a fraction, the main property of the fraction is used.
Consider simple examples:

In these examples, we immediately see how one of the fractions can be converted to get equal denominators.
If we designate ways to reduce fractions to one denominator, then this one will be called METHOD ONE.
That is, immediately when “evaluating” the fraction, you need to figure out whether such an approach will work - we check whether the larger denominator is divisible by the smaller one. And if it is divided, then we perform the transformation - we multiply the numerator and denominator so that the denominators of both fractions become equal.
Now look at these examples:
This approach does not apply to them. There are other ways to reduce fractions to a common denominator, consider them.
Method SECOND.
Multiply the numerator and denominator of the first fraction by the denominator of the second, and the numerator and denominator of the second fraction by the denominator of the first:

*In fact, we bring fractions to the form when the denominators become equal. Next, we use the rule of adding timid with equal denominators.
Example:
*This method can be called universal, and it always works. The only negative is that after the calculations, a fraction may turn out that will need to be further reduced.
Consider an example:
It can be seen that the numerator and denominator are divisible by 5:

Method THIRD.
Find the least common multiple (LCM) of the denominators. This will be the common denominator. What is this number? This is the smallest natural number that is divisible by each of the numbers.
Look, here are two numbers: 3 and 4, there are many numbers that are divisible by them - these are 12, 24, 36, ... The smallest of them is 12. Or 6 and 15, 30, 60, 90 are divisible by them .... Least 30. Question - how to determine this least common multiple?
There is a clear algorithm, but often this can be done immediately without calculations. For example, according to the above examples (3 and 4, 6 and 15), no algorithm is needed, we took large numbers (4 and 15), doubled them and saw that they are divisible by the second number, but pairs of numbers can be others, such as 51 and 119.
Algorithm. In order to determine the least common multiple of several numbers, you must:
- decompose each of the numbers into SIMPLE factors
- write out the decomposition of the BIGGER of them
- multiply it by the MISSING factors of other numbers
Consider examples:
50 and 60 50 = 2∙5∙5 60 = 2∙2∙3∙5
in decomposition more missing one five
=> LCM(50,60) = 2∙2∙3∙5∙5 = 300
48 and 72 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3
in the expansion of a larger number, two and three are missing
=> LCM(48,72) = 2∙2∙2∙2∙3∙3 = 144
* The least common multiple of two prime numbers is equal to their product
Question! And why is it useful to find the least common multiple, because you can use the second method and simply reduce the resulting fraction? Yes, you can, but it's not always convenient. See what the denominator will be for the numbers 48 and 72 if you simply multiply them 48∙72 = 3456. Agree that it is more pleasant to work with smaller numbers.
Consider examples:
*51 = 3∙17 119 = 7∙17
in the expansion of a larger number, a triple is missing
=> LCM(51,119) = 3∙7∙17
And now we apply the first method:
* Look at the difference in the calculations, in the first case there is a minimum of them, and in the second you need to work separately on a piece of paper, and even the fraction that you got needs to be reduced. Finding the LCM simplifies the work considerably.
More examples:

* In the second example, it is already clear that the smallest number that is divisible by 40 and 60 is 120.
TOTAL! GENERAL CALCULATION ALGORITHM!
- we bring fractions to ordinary ones, if there is an integer part.
- we bring fractions to a common denominator (first we look to see if one denominator is divisible by another, if it is divisible, then we multiply the numerator and denominator of this other fraction; if it is not divisible, we act through the other methods indicated above).
- having received fractions with equal denominators, we perform actions (addition, subtraction).
- if necessary, we reduce the result.
- if necessary, select the whole part.
2. Product of fractions.
The rule is simple. When multiplying fractions, their numerators and denominators are multiplied:
 Examples:
Examples:
Task. 13 tons of vegetables were brought to the base. Potatoes make up ¾ of all imported vegetables. How many kilograms of potatoes were brought to the base?
Let's finish with the work.
*Earlier I promised you to give a formal explanation of the main property of the fraction through the product, please:

3. Division of fractions.
The division of fractions is reduced to their multiplication. It is important to remember here that the fraction that is a divisor (the one that is divided by) is turned over and the action changes to multiplication:

This action can be written as a so-called four-story fraction, because the division itself “:” can also be written as a fraction:

Examples:
That's all! Good luck to you!
Sincerely, Alexander Krutitskikh.
DECIMAL FRACTIONS. ACTIONS ON DECIMAL FRACTIONS
(lesson summary)
Tumysheva Zamira Tansykbaevna, teacher of mathematics, school-gymnasium No. 2
Khromtau, Aktobe region, Republic of Kazakhstan
This lesson development is intended as a generalization lesson for the chapter “Actions on decimals". It can be used in both 5th grade and 6th grade. The lesson is conducted in the form of a game.
Decimals. Operations on decimals.(lesson summary)
Target:
Practicing the skills and abilities of adding, subtracting, multiplying and dividing decimal fractions into natural numbers and decimal fractions
Creation of conditions for skills development independent work, self-control and self-esteem, development of intellectual qualities: attention, imagination, memory, ability to analyze and generalize
To instill cognitive interest in the subject and develop self-confidence
LESSON PLAN:
1. Organizational part.
3. The theme and purpose of our lesson.
4. The game "To the treasured flag!"
5. The game "Number mill".
6. Lyrical digression.
8. Game "Encryption" (work in pairs)
9. Summing up.
10. Homework.
1. Organizational part. Hello. Have a seat.
2. An overview of the rules for performing arithmetic operations with decimal fractions.
Rule for adding and subtracting decimals:
1) equalize the number of decimal places in these fractions;
2) write down one under the other so that the comma is under the comma;
3) without noticing the comma, perform the action (addition or subtraction), and put a comma under the commas as a result.
3,455 + 0,45 = 3,905 3,5 + 4 = 7,5 15 – 7,88 = 7,12 4,57 - 3,2 = 1,37
3,455 + 3,5 _15,00 _ 4,57
0,450 4,0 7,88 3,20
3,905 7,5 7,12 1,37
When adding and subtracting, natural numbers are written as a decimal fraction with decimal places equal to zero.
Rule for multiplying decimals:
1) ignoring the comma, multiply the numbers;
2) in the resulting product, separate with a comma as many digits from right to left as they are separated by a comma in decimal fractions.
When multiplying a decimal fraction by bit units (10, 100, 1000, etc.), the comma is moved to the right by as many numbers as there are zeros in the bit unit
4
17.25 4 = 69
x 1 7.2 5
4
6 9,0 0
15.256 100 = 1525.6
.5 0.52 = 2.35X 0.5 2
4,5
2 7 0
2 0 8__
2,3 5 0
When multiplying, natural numbers are written as natural numbers.
The rule for dividing decimal fractions by a natural number:
1) divide the whole part of the dividend, put a comma in the private;
2) continue dividing.
When dividing to the remainder, we take down only one number from the dividend.
If in the process of dividing a decimal fraction there remains a remainder, then by assigning the required number of zeros to it, we continue the division until the remainder is zero.
15,256: 100 = 0,15256
0,25: 1000 = 0,00025
When dividing a decimal fraction into bit units (10, 100, 1000, etc.), the comma is moved to the left by as many numbers as there are zeros in the bit unit.
18,4: 8 = 2,3
_ 18,4 І_8_
16 2,3
2 4
2 4
22,2: 25 = 0,88
22,2 І_25_
0 0,888
22 2
20 0
2 20
2 00
200
200
3,56: 4 = 0,89
3,56 І_4_
0 0,89
3 5
3 2
36
When dividing, natural numbers are written as natural numbers.
Rule for dividing decimals by decimals:
1) we move the comma in the divisor to the right so that we get a natural number;
2) move the comma in the dividend to the right of as many numbers as it was moved in the divisor;
3) we divide the decimal fraction by a natural number.
3,76: 0,4 = 9, 4
_ 3,7,6 I_0,4,_
3 6 9, 4
1 6
1 6
0
The game "To the cherished flag!"
Rules of the game: From each team, one student is called to the board, who perform an oral count from the bottom step. The solver of one example marks the answer in the table. Then he is replaced by another member of the team. There is a movement up - to the coveted flag. Students in the field verbally check the results of their players. If the answer is incorrect, another member of the team comes to the board to continue solving the tasks. Team captains call the students to work at the board. The first team to reach the flag with the fewest students wins.
Game "Number Mill"
Rules of the game: Numbers are written in the circles of the mill. The arrows connecting the circles indicate the actions. The task is to perform sequential actions, moving along the arrow from the center to the outer circle. Performing sequential actions along the indicated route, you will find the answer in one of the circles below. The result of performing actions for each arrow is written in the oval next to it.

Lyrical digression.
Lifshitz's poem "Three tenths"
Who is this
From portfolio
Throws in annoyance
hateful puzzler,
Pencil case and notebooks
And sticks his diary.
Without blushing,
Under an oak sideboard.
To lie under the sideboard? ..
Please get to know:
Kostya Zhigalin.
The victim of eternal nit-picking, -
He failed again.
And hisses
To disheveled
Looking problem book:
I'm just not lucky!
I'm just a loser!
What is the reason
His resentment and annoyance?
That the answer didn't fit
Only three tenths.
This is a real waste!
And to him, of course,
find fault
Strict
Maria Petrovna.
Three tenths...
Tell me about this error
And, perhaps, on the faces
You will see a smile.
Three tenths...
And yet about this error
I beg you
listen to me
No smile.
If b, building your house.
The one you live in.
Architect
a little
Wrong
In counting, -
What would happen.
Do you know Kostya Zhigalin?
This house
would have turned
In a heap of ruins!
You enter the bridge.
He is reliable and durable.
Don't be an engineer
Accurate in his drawings, -
Would you, Kostya,
Falling down
into the cold river
Wouldn't say thank you
That person!
Here is the turbine.
It has a shaft
Bored by turners.
If the turner
In work
Wasn't very accurate.
It would be done, Kostya,
Great misfortune:
It would destroy the turbine
into small parts!
Three tenths -
And the walls
Are being erected
Koso!
Three tenths -
And collapse
wagons
Off the slope!
make a mistake
Only three tenths
Pharmacy, -
Medicine becomes poison
Will kill a man!
We smashed and drove
Fascist gang.
Your father gave
Battery command.
Make a mistake on arrival
At least three tenths
The shells would not overtake
Damned fascists.
You think about it
My friend, in cold blood
And say.
Was it not right
Maria Petrovna?
Honestly
Think about it, Kostya.
It's not long to lie
Diary under the buffet!
Test work on the topic "Decimal fractions" (mathematics -5)
9 slides will appear on the screen in sequence. Students write down the number of the option and the answers to the question in their notebooks. For example, Option 2
1. C; 2. A; and so on.
QUESTION 1
Option 1
When multiplying a decimal fraction by 100, you need to move the comma in this fraction:
A. to the left by 2 digits; B. to the right by 2 digits; C. do not change the place of the comma.
Option 2
When multiplying a decimal fraction by 10, you need to move the comma in this fraction:
A. right 1 digit; B. to the left by 1 digit; C. do not change the place of the comma.
QUESTION 2
Option 1
The sum 6.27 + 6.27 + 6.27 + 6.27 + 6.27 as a product is written as follows:
A. 6.27 5; B. 6.27 6.27; S. 6.27 4.
Option 2
The sum 9.43 + 9.43 + 9.43 + 9.43 as a product is written as follows:
A. 9.43 9.43; B. 6 9.43; S. 9.43 4.
QUESTION 3
Option 1
In the product 72.43 18 after the decimal point will be:
Option 2
In the product of 12.453 35 after the decimal point will be:
A. 2 digits; B. 0 digits; C. 3 digits.
QUESTION 4
Option 1
In quotient 76.4:2 after the decimal point will be:
A. 2 digits; B. 0 digits; C. 1 digit.
Option 2
In private 95.4:6 after the decimal point will be:
A. 1 digit; B. 3 digits; C. 2 digits.
QUESTION 5
Option 1
Find the value of the expression 34.5: x + 0.65 y, at x=10 y=100:
A. 35.15; B. 68.45; S. 9.95.
Option 2
Find the value of the expression 4.9 x +525:y, at x=100 y=1000:
A. 4905.25; B. 529.9; pp. 490,525.
QUESTION 6
Option 1
The area of a rectangle with sides 0.25 and 12 cm is
A. 3; B. 0.3; S. 30.
Option 2
The area of a rectangle with sides 0.5 and 36 cm is
A. 1.8; V. 18; C. 0.18.
QUESTION 7
Option 1
from school at the same time opposite sides two students left. The speed of the first student is 3.6 km/h, the speed of the second student is 2.56 km/h. After 3 hours the distance between them will be:
A. 6.84 km; V. 18.48 km; S. 3.12 km
Option 2
Two cyclists left the school at the same time in opposite directions. The speed of the first is 11.6 km/h, the speed of the second is 13.06 km/h. After 4 hours the distance between them will be:
A. 5.84 km; V. 100.8 km; S. 98.64 km
Option 1
Option 2
Check your answers. Put a "+" for a correct answer and a "-" for an incorrect answer.
Game "Encryption"
Rules of the game: Each desk is given a card with a task that has a code-letter. After completing the steps and getting the result, write down the code-letter of your card under the number corresponding to your answer.
As a result, we get the proposal:
6,8
420
21,6
420
306
65,8
21,6
Summing up the lesson.
Scores for test work are announced.
Homework #1301, 1308, 1309
Thank you for your attention!!!
This article is about decimals. Here we will deal with decimal notation fractional numbers, we introduce the concept of a decimal fraction and give examples of decimal fractions. Next, let's talk about the digits of decimal fractions, give the names of the digits. After that, we will focus on infinite decimal fractions, say about periodic and non-periodic fractions. Next, we list the main actions with decimal fractions. In conclusion, we establish the position of decimal fractions on the coordinate ray.
Page navigation.
Decimal notation of a fractional number
Reading decimals
Let's say a few words about the rules for reading decimal fractions.
Decimal fractions, which correspond to the correct ordinary fractions, are read in the same way as these ordinary fractions, only “zero whole” is added beforehand. For example, the decimal fraction 0.12 corresponds to the ordinary fraction 12/100 (it reads “twelve hundredths”), therefore, 0.12 is read as “zero point twelve hundredths”.
Decimal fractions, which correspond to mixed numbers, are read in exactly the same way as these mixed numbers. For example, the decimal fraction 56.002 corresponds to a mixed number, therefore, the decimal fraction 56.002 is read as "fifty-six point two thousandths."
Places in decimals
In the notation of decimal fractions, as well as in the notation of natural numbers, the value of each digit depends on its position. Indeed, the number 3 in decimal 0.3 means three tenths, in decimal 0.0003 - three ten thousandths, and in decimal 30,000.152 - three tens of thousands. Thus, we can talk about digits in decimals, as well as about digits in natural numbers.
The names of the digits in the decimal fraction to the decimal point completely coincide with the names of the digits in natural numbers. And the names of the digits in the decimal fraction after the decimal point are visible from the following table.

For example, in the decimal fraction 37.051, the number 3 is in the tens place, 7 is in the units place, 0 is in the tenth place, 5 is in the hundredth place, 1 is in the thousandth place.
The digits in the decimal fraction also differ in seniority. If we move from digit to digit from left to right in the decimal notation, then we will move from senior To junior ranks. For example, the hundreds digit is older than the tenths digit, and the millionths digit is younger than the hundredths digit. In this final decimal fraction, we can talk about the most significant and least significant digits. For example, in decimal 604.9387 senior (highest) the digit is the hundreds digit, and junior (lowest)- ten-thousandth place.
For decimal fractions, expansion into digits takes place. It is analogous to the expansion in digits of natural numbers. For example, the decimal expansion of 45.6072 is: 45.6072=40+5+0.6+0.007+0.0002 . And the properties of addition from the expansion of a decimal fraction by digits allow you to go to other representations of this decimal fraction, for example, 45.6072=45+0.6072 , or 45.6072=40.6+5.007+0.0002 , or 45.6072= 45.0072+0.6 .
End decimals
Up to this point, we have only talked about decimal fractions, in the record of which there is a finite number of digits after the decimal point. Such fractions are called final decimal fractions.
Definition.
End decimals- These are decimal fractions, the records of which contain a finite number of characters (digits).
Here are some examples of final decimals: 0.317 , 3.5 , 51.1020304958 , 230 032.45 .
However, not every common fraction can be represented as a finite decimal fraction. For example, the fraction 5/13 cannot be replaced by an equal fraction with one of the denominators 10, 100, ..., therefore, it cannot be converted to a final decimal fraction. We'll talk more about this in the theory section of converting ordinary fractions to decimal fractions.
Infinite decimals: periodic fractions and non-periodic fractions
In writing a decimal fraction after a decimal point, you can allow the possibility of an infinite number of digits. In this case, we will come to the consideration of the so-called infinite decimal fractions.
Definition.
Endless decimals- These are decimal fractions, in the record of which there is an infinite number of digits.
It is clear that we cannot write the infinite decimal fractions in full, therefore, in their recording they are limited to only a certain finite number of digits after the decimal point and put an ellipsis indicating an infinitely continuing sequence of digits. Here are some examples of infinite decimal fractions: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.111111111…, 69.74152152152….
If you look closely at the last two endless decimal fractions, then in the fraction 2.111111111 ... the infinitely repeating number 1 is clearly visible, and in the fraction 69.74152152152 ..., starting from the third decimal place, the repeating group of numbers 1, 5 and 2 is clearly visible. Such infinite decimal fractions are called periodic.
Definition.
Periodic decimals(or simply periodic fractions) are infinite decimal fractions, in the record of which, starting from a certain decimal place, some digit or group of digits, which is called fraction period.
For example, the period of the periodic fraction 2.111111111… is the number 1, and the period of the fraction 69.74152152152… is a group of numbers like 152.
For infinite periodic decimal fractions, a special notation has been adopted. For brevity, we agreed to write the period once, enclosing it in parentheses. For example, the periodic fraction 2.111111111… is written as 2,(1) , and the periodic fraction 69.74152152152… is written as 69.74(152) .
It is worth noting that for the same periodic decimal fraction, you can specify different periods. For example, the periodic decimal 0.73333… can be considered as a fraction 0.7(3) with a period of 3, as well as a fraction 0.7(33) with a period of 33, and so on 0.7(333), 0.7 (3333), ... You can also look at the periodic fraction 0.73333 ... like this: 0.733(3), or like this 0.73(333), etc. Here, in order to avoid ambiguity and inconsistencies, we agree to consider as the period of a decimal fraction the shortest of all possible sequences of repeating digits, and starting from the closest position to the decimal point. That is, the period of the decimal fraction 0.73333… will be considered a sequence of one digit 3, and the periodicity starts from the second position after the decimal point, that is, 0.73333…=0.7(3) . Another example: the periodic fraction 4.7412121212… has a period of 12, the periodicity starts from the third digit after the decimal point, that is, 4.7412121212…=4.74(12) .
Infinite decimal periodic fractions are obtained when converted to decimal fractions ordinary fractions, whose denominators contain prime factors other than 2 and 5 .
Here it is worth mentioning periodic fractions with a period of 9. Here are examples of such fractions: 6.43(9) , 27,(9) . These fractions are another notation for periodic fractions with period 0, and it is customary to replace them with periodic fractions with period 0. To do this, period 9 is replaced by period 0, and the value of the next highest digit is increased by one. For example, a fraction with period 9 of the form 7.24(9) is replaced by a periodic fraction with period 0 of the form 7.25(0) or an equal final decimal fraction of 7.25. Another example: 4,(9)=5,(0)=5 . The equality of a fraction with a period of 9 and its corresponding fraction with a period of 0 is easily established after replacing these decimal fractions with their equal ordinary fractions.
Finally, let's take a closer look at infinite decimals, which do not have an infinitely repeating sequence of digits. They are called non-periodic.
Definition.
Non-recurring decimals(or simply non-periodic fractions) are infinite decimals with no period.
Sometimes non-periodic fractions have a form similar to that of periodic fractions, for example, 8.02002000200002 ... is a non-periodic fraction. In these cases, you should be especially careful to notice the difference.
Note that non-periodic fractions are not converted to ordinary fractions, infinite non-periodic decimal fractions represent irrational numbers.
Operations with decimals
One of the actions with decimals is comparison, and four basic arithmetic are also defined operations with decimals: addition, subtraction, multiplication and division. Consider separately each of the actions with decimal fractions.
Decimal Comparison essentially based on a comparison of ordinary fractions corresponding to the compared decimal fractions. However, converting decimal fractions to ordinary ones is a rather laborious operation, and infinite non-repeating fractions cannot be represented as an ordinary fraction, so it is convenient to use a bitwise comparison of decimal fractions. Bitwise comparison of decimals is similar to comparison of natural numbers. For more detailed information, we recommend that you study the article material comparison of decimal fractions, rules, examples, solutions.
Let's move on to the next step - multiplying decimals. Multiplication of final decimal fractions is carried out similarly to the subtraction of decimal fractions, rules, examples, solutions to multiplication by a column of natural numbers. In the case of periodic fractions, multiplication can be reduced to the multiplication of ordinary fractions. In turn, the multiplication of infinite non-periodic decimal fractions after their rounding is reduced to the multiplication of finite decimal fractions. We recommend further study of the material of the article multiplication of decimal fractions, rules, examples, solutions.
Decimals on the coordinate beam
There is a one-to-one correspondence between dots and decimals.
Let's figure out how points are constructed on the coordinate ray corresponding to a given decimal fraction.
We can replace finite decimal fractions and infinite periodic decimal fractions with ordinary fractions equal to them, and then construct the corresponding ordinary fractions on the coordinate ray. For example, a decimal fraction 1.4 corresponds to an ordinary fraction 14/10, therefore, the point with coordinate 1.4 is removed from the origin in the positive direction by 14 segments equal to a tenth of a single segment.

Decimal fractions can be marked on the coordinate beam, starting from the expansion of this decimal fraction into digits. For example, let's say we need to build a point with coordinate 16.3007 , since 16.3007=16+0.3+0.0007 , then in given point can be reached by sequentially laying 16 unit segments from the origin, 3 segments, the length of which is equal to a tenth of a unit segment, and 7 segments, the length of which is equal to a ten-thousandth fraction of a unit segment.
This method of constructing decimal numbers on the coordinate beam allows you to get as close as you like to the point corresponding to an infinite decimal fraction.
It is sometimes possible to accurately plot a point corresponding to an infinite decimal. For example, ![]() , then this infinite decimal fraction 1.41421... corresponds to the point of the coordinate ray, remote from the origin by the length of the diagonal of a square with a side of 1 unit segment.
, then this infinite decimal fraction 1.41421... corresponds to the point of the coordinate ray, remote from the origin by the length of the diagonal of a square with a side of 1 unit segment.
The reverse process of obtaining a decimal fraction corresponding to a given point on the coordinate beam is the so-called decimal measurement of a segment. Let's see how it is done.
Let our task be to get from the origin to a given point on the coordinate line (or infinitely approach it if it is impossible to get to it). With a decimal measurement of a segment, we can sequentially postpone any number of unit segments from the origin, then segments whose length is equal to a tenth of a single segment, then segments whose length is equal to a hundredth of a single segment, etc. By writing down the number of plotted segments of each length, we get the decimal fraction corresponding to a given point on the coordinate ray.
For example, to get to point M in the above figure, you need to set aside 1 unit segment and 4 segments, the length of which is equal to the tenth of the unit. Thus, the point M corresponds to the decimal fraction 1.4.
It is clear that the points of the coordinate beam, which cannot be reached during the decimal measurement, correspond to infinite decimal fractions.
Bibliography.
- Mathematics: studies. for 5 cells. general education institutions / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21st ed., erased. - M.: Mnemosyne, 2007. - 280 p.: ill. ISBN 5-346-00699-0.
- Mathematics. Grade 6: textbook. for general education institutions / [N. Ya. Vilenkin and others]. - 22nd ed., Rev. - M.: Mnemosyne, 2008. - 288 p.: ill. ISBN 978-5-346-00897-2.
- Algebra: textbook for 8 cells. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; ed. S. A. Telyakovsky. - 16th ed. - M. : Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Mathematics (a manual for applicants to technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.
In mathematics, various types of numbers have been studied since their inception. There are a large number of sets and subsets of numbers. Among them are integers, rational, irrational, natural, even, odd, complex and fractional. Today we will analyze information about the last set - fractional numbers.
Definition of fractions
Fractions are numbers consisting of a whole part and fractions of a unit. Just like integers, there are an infinite number of fractional numbers between two integers. In mathematics, operations with fractions are performed, since with integers and natural numbers. It is quite simple and can be learned in a couple of lessons.
The article presents two types
Common fractions
Ordinary fractions are the integer part a and two numbers written through the fractional bar b/c. Common fractions can be extremely handy if the fractional part cannot be represented in rational decimal form. In addition, it is more convenient to perform arithmetic operations through a fractional line. The top part is called the numerator, the bottom part is the denominator.
Actions with ordinary fractions: examples
Basic property of a fraction. At multiplying the numerator and denominator by the same number that is not zero, the result is a number equal to the given one. This property of a fraction helps to bring a denominator for addition (this will be discussed below) or reduce a fraction, making it more convenient for counting. a/b = a*c/b*c. For example, 36/24 = 6/4 or 9/13 = 18/26
Reduction to a common denominator. To bring the denominator of a fraction, you need to represent the denominator in the form of factors, and then multiply by the missing numbers. For example, 7/15 and 12/30; 7/5*3 and 12/5*3*2. We see that the denominators differ by two, so we multiply the numerator and denominator of the first fraction by 2. We get: 14/30 and 12/30.
Compound fractions- ordinary fractions with highlighted whole part. (A b/c) To represent a compound fraction as a common fraction, multiply the number in front of the fraction by the denominator and then add it to the numerator: (A*c + b)/c.

Arithmetic operations with fractions
It will not be superfluous to consider the well-known arithmetic operations only when working with fractional numbers.
Addition and subtraction. Adding and subtracting fractions is just as easy as whole numbers, with the exception of one difficulty - the presence of a fractional line. When adding fractions with the same denominator, it is necessary to add only the numerators of both fractions, the denominators remain unchanged. For example: 5/7 + 1/7 = (5+1)/7 = 6/7
If the denominators of two fractions are different numbers, you first need to bring them to a common one (as discussed above). 1/8 + 3/2 = 1/2*2*2 + 3/2 = 1/8 + 3*4/2*4 = 1/8 + 12/8 = 13/8. Subtraction occurs according to exactly the same principle: 8/9 - 2/3 \u003d 8/9 - 6/9 \u003d 2/9.

Multiplication and division. Actions with fractions by multiplication occur according to the following principle: numerators and denominators are multiplied separately. IN general view the multiplication formula looks like this: a/b *c/d = a*c/b*d. In addition, as you multiply, you can reduce the fraction by eliminating the same factors from the numerator and denominator. In another language, the numerator and denominator are divisible by the same number: 4/16 = 4/4*4 = 1/4.
To divide one ordinary fraction by another, you need to change the numerator and denominator of the divisor and perform the multiplication of two fractions, according to the principle discussed earlier: 5/11: 25/11 = 5/11 * 11/25 = 5*11/11*25 = 1/5
Decimals
Decimals are the more popular and commonly used version of fractional numbers. They are easier to write down in a line or present on a computer. The structure of the decimal fraction is as follows: first the whole number is written, and then, after the decimal point, the fractional part is written. At their core, decimal fractions are compound fractions, but their fractional part is represented by a number divided by a multiple of 10. Hence their name. Operations with decimal fractions are similar to operations with integers, since they are also written in the decimal number system. Also, unlike ordinary fractions, decimals can be irrational. This means that they can be infinite. They are written as 7,(3). The following entry is read: seven whole, three tenths in the period.
Basic operations with decimal numbers
Addition and subtraction of decimal fractions. Performing actions with fractions is no more difficult than with whole natural numbers. The rules are exactly the same as those used when adding or subtracting natural numbers. They can also be considered a column in the same way, but if necessary, replace the missing places with zeros. For example: 5.5697 - 1.12. In order to perform a column subtraction, you need to equalize the number of numbers after the decimal point: (5.5697 - 1.1200). So, the numerical value will not change and can be counted in a column.
Operations with decimal fractions cannot be performed if one of them has an irrational form. To do this, you need to convert both numbers to ordinary fractions, and then use the techniques described earlier.

Multiplication and division. Multiplying decimals is similar to multiplying natural numbers. They can also be multiplied by a column, simply ignoring the comma, and then separated by a comma in the final value the same number of digits as the sum after the decimal point was in two decimal fractions. For example, 1.5 * 2.23 = 3.345. Everything is very simple, and should not cause difficulties if you have already mastered the multiplication of natural numbers.
Division also coincides with the division of natural numbers, but with a slight digression. To split into decimal number column, you must discard the comma in the divisor, and multiply the dividend by the number of digits after the decimal point in the divisor. Then perform division as with natural numbers. With incomplete division, you can add zeros to the dividend on the right, also adding a zero after the decimal point.
Examples of actions with decimal fractions. Decimals are a very handy tool for arithmetic counting. They combine the convenience of natural, whole numbers and the precision of common fractions. In addition, it is quite simple to convert one fraction to another. Operations with fractions are no different from operations with natural numbers.
- Addition: 1.5 + 2.7 = 4.2
- Subtraction: 3.1 - 1.6 = 1.5
- Multiplication: 1.7 * 2.3 = 3.91
- Division: 3.6: 0.6 = 6
In addition, decimals are suitable for representing percentages. So, 100% = 1; 60% = 0.6; and vice versa: 0.659 = 65.9%.

That's all you need to know about fractions. The article considered two types of fractions - ordinary and decimal. Both are fairly easy to calculate, and if you have a complete mastery of natural numbers and operations with them, you can safely start learning fractional ones.





