 It is believed that the problem of stereometry on profile exam in mathematics - only for excellent students. That its solution requires special talents and mysterious “spatial thinking”, which only rare lucky people possess from birth.
It is believed that the problem of stereometry on profile exam in mathematics - only for excellent students. That its solution requires special talents and mysterious “spatial thinking”, which only rare lucky people possess from birth.
Is it so?
Fortunately, everything is much simpler. What is so beautifully called " spatial thinking”, most often means knowledge of the basics of stereometry and the ability to build drawings.
First, knowledge of stereometry formulas is necessary. In our tables " Polyhedrons"And" Bodies of revolution"All the formulas are given by which the volumes and surface areas of three-dimensional bodies are calculated.
Secondly - confident solution of problems in geometry presented in Part 1 (the first 12 USE tasks). These are both planimetric and stereometric problems.
And most importantly, to solve Problem 14, you will need the basic axioms and theorems of stereometry. It is best if you purchase a textbook on geometry for grades 10-11 (author - A. V. Pogorelov or L. S. Atanasyan), and answer the questions listed below. Write down the definitions and statements of theorems in your notebook. Make drawings. Try to prove the theorem yourself.
Working on this task, formulate for yourself - what is the difference between definition and sign. There is, for example, a definition of parallelism of a straight line and a plane - and a sign of parallelism of a straight line and a plane. What is the difference between them?
It is very good if you do the task yourself, and then check with the answers. All answers can be found on our website, in this section.
Stereometry program.
- Plane in space. Finish the phrase: A plane can be drawn through ...
(Give four answers).
- Location of planes in space. Finish the sentence: If two planes have common point then they...
- Parallelism of a line and a plane. Definition and sign.
- What is oblique and oblique projection. Drawing.
- The angle between a line and a plane.
- Perpendicularity of a line and a plane. Definition and sign.
- Crossing straight lines. Angle between intersecting lines. Distance between intersecting lines.
- The distance from a straight line to a plane parallel to it.
- Parallelism of planes. Definition and sign.
- Plane perpendicularity. Definition and sign.
- Finish the sentence: a) Lines of intersection of two parallel planes by a third plane...
b) Segments of parallel lines enclosed between parallel planes...
Here are a few simple rules for solving problems in stereometry:
There are two main ways to solve problems in stereometry on the exam in mathematics. The first is classical: the practical application of definitions, theorems and features, the list of which is given above. Second -
C2 USE in Mathematics.
The base of the pyramid is a square
two side faces of this pyramid are perpendicular to the plane of its base,
its other two side faces form equal dihedral angles with the base plane,
each of which is equal to 30 degrees.
The height of the pyramid is sqrt(2).
Find the area of the side surface of the pyramid.
Solution C2 Unified State Examination in Mathematics.
C2 USE in Mathematics.
The diameter of the circumference of the base of the cylinder is 26, the generatrix of the cylinder is 21. The plane intersects its bases along chords of length 24 and 10. Find the tangent of the angle between this plane and the plane of the base of the cylinder.
Solution C2 Unified State Examination in Mathematics.

Let AB=10 and C1D1 = 24 be the chords along which the section intersects the bases of the cylinder. The planes of the bases are parallel, so AB and C1D1 are also parallel.
Dropping the perpendiculars from the points C1 and D1 to the plane OAB, we obtain the segment CD equal to C1D1. Let K, L, and L1 be the midpoints of the chords AB, CD, and C1D1, respectively.
The angle between the section plane and the base plane of the cylinder will be equal to the angle L1KL. We will find its tangent from the right triangle L1LK: tg(L1KL) = LL1/LK.
LL1 = cylinder generatrix = 21
LK=LO+OK.
From right triangle CLO:
LO = sqrt(CO^2-CL^2) = sqrt(13^2-12^2) = 5
From right triangle AKO:
OK = sqrt(AO^2-AK^2) = sqrt(13^2-5^2) = 12
Tg(L1KL) = LL1/LK = 21/17
Task C2 Condition:
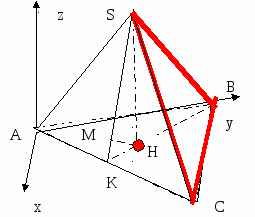
In a regular hexagonal pyramid SABCDEF
base side AB=√3, side edge SA = √7. Find the distance from vertex A to plane BCS.
Solution:
Note that AD is parallel to BC, and hence to the entire plane BCS.
This means that all points of the line AD are equidistant from the plane BCS.
Let SH be the height of triangle BCS, SO be the perpendicular dropped from the point S to the plane of the base of the pyramid, and the point O belongs to AD. The desired distance will be the length of the height OM of the right triangle SOH.
1) Find OH from an equilateral triangle OBC: OH = BC*sqrt(3)/2 = 3/2
2) Find SH from right triangle BHS: SH = sqrt(SB^2-BH^2) = sqrt(sqrt(7)^2-(sqrt(3)/2)^2) = 5/2
3) Find SO from right triangle SOH: SO = sqrt(SH^2-OH^2) = 4/2
4) The desired distance OM, knowing all the sides of the right triangle SOH, can, for example, be found by writing the expression for its area in two different ways:
S \u003d SO * OH / 2 \u003d SH * OM / 2,
Where OM = SO*OH/SH = 4*3/5 = 6/5
Answer: 6/5
Task C2 Condition:
In a regular triangular pyramid ABCS with a base ABC, the edges are known: AB \u003d 5 roots out of 3, SC \u003d 13.
Find the angle formed by the plane of the base and the straight line passing through the midpoint of the edges AS and BC.
Solution:
1. Since SABC is a regular pyramid, then ABC is an equilateral triangle, and the remaining faces are equal isosceles triangles.
That is, all sides of the base are 5*sqrt(3), and all side ribs are equal to 13.
2. Let D be the midpoint of BC, E the midpoint of AS, SH the height from point S to the base of the pyramid, Ep the height from point E to the base of the pyramid.
3. Find AD from the right triangle CAD using the Pythagorean theorem. You get 15/2 = 7.5.
4. Since the pyramid is regular, point H is the intersection point of heights/medians/bisectors of triangle ABC, which means it divides AD in the ratio 2:1 (AH=2*AD).
5. Find SH from right triangle ASH. AH=AD*2/3 = 5, AS = 13, by the Pythagorean theorem SH = sqrt(13^2-5^2) = 12.
6. Triangles AEp and ASH are both right-angled and have a common angle A, hence similar. By assumption, AE = AS/2, hence both Ap = AH/2 and Ep = SH/2.
7. It remains to consider the right triangle EDp (we are just interested in the angle EDp).
Ep = SH/2 = 6;
Dp = AD*2/3 = 5;
Angle tangent EDp = Ep/Dp = 6/5,
Angle EDp = arctg(6/5)
Answer:
Task C2 Condition:
in isosceles right triangle one of the legs lies in plane a, and the other forms an angle of 45 degrees with it. Find the angle between the hypotenuse of the given triangle and the given plane.
Solution:
Triangle ABC, angle C - right, BC belongs to the plane.
AC = BC = x, AB = x*sqrt(2)
Let us drop the perpendicular AA1 to the plane a.
The desired angle is the angle A1BA.
Angle A1CA is 45 degrees, angle AA1C is a right angle. AA1 = AC*sin(45 degrees) = x/sqrt(2).
sin(A1BA) = AA1/AB = (x/sqrt(2))/(x*sqrt(2)) = 1/2
Angle A1BA = arcsin(1/2) = 30 degrees.
Methodical development of solving problems C2 at the Unified State Examination in mathematics.
Explanatory note
Task C2 refers to tasks advanced level Difficulties with a detailed answer.
When performing a task in the answer form No. 2, a complete justified decision and answer should be recorded. It is required that the calculations made be consistent and logical, the key points of the decision are justified, and mathematical terms and symbols are used correctly. Problem C2 is a stereometric problem of medium complexity, feasible for most successful graduates. A complete correct solution of problem C2 is estimated at 2 points.
The assessment of the fulfillment of the tasks of the second part is carried out by experts on the basis of a specially developed system of criteria based on the following requirements. The method and form of writing the solution can be arbitrary, but the solution must be mathematically literate, complete and justified. At the same time, the progress of the graduate in solving the problem is evaluated. When solving a problem, you can use without proofs and references any mathematical facts contained in textbooks and teaching aids approved or recommended by the Ministry of Education and Science of the Russian Federation.
Build a drawing that matches the condition (if possible, the most visual),
Describe the figure, remember the definition, properties, signs,
Determine dependencies between elements
Reason from the question of the problem, gradually using the given conditions.
IN last years when solving C2 problems, it is often required to find the distance and angles:
From point to line;
From point to plane;
Between intersecting lines, or find the angle between:
Straight & Plane & Angle;
Planes and angle.
For many modern students, it is a difficult task to be able to navigate in geometric concepts, theorems, signs, or to make the necessary constructions, and as a rule, it is easier for them to learn a certain set of formulas and use one algorithm. Therefore, I want to propose an algorithm for solving C2 based on the coordinate method, which does not require any construction, but is analytical.
The work is aimed at preparing students for the exam. It considers: examples of solving problems for finding the distance between intersecting lines, the angle between complex planes, the angle between a line and a plane. Solutions to problems follow from the analysis of theoretical material. The proposed tasks can be considered in the lessons allotted for preparing students for the exam and in the lessons on the topics: "The angle between a straight line and a plane", "The angle between planes", "The distance between criss-crossing lines".
Theoretical material
Finding distances:
Point to line
1 way - vector
M1(x1, y1, z1) - an arbitrary point in space from which you need to find the distance to the line ℓ. Point M0 (x0, y0, z0), an arbitrary point belonging to the line ℓ, (a , b , c ) - coordinates of the directing vector of the line ℓ.
2 way - analytical
1. Construct a triangle from a line and a point, i.e. connect the point from which we are looking for the distance with any two points on the line
2. We are looking for all sides of the resulting triangle using the formula for the distances between two points:
3. Then, using the cosine theorem, we look for the cosine of any angle of the triangle
4. Using the main trigonometric identity find the sine of this angle
5. According to the formula S \u003d 1 / 2ab sin a area of this triangle
6. We are looking for the height extended from a given point to a given straight line using the area of the triangle S = 1/2ah
Example
In a regular hexagonal prism ABCDEF A1B1C1D 1E 1F whose base sides are 4 and the side edges are 1, find the distance from point B to the line F 1 E 1.

1 way
SA= 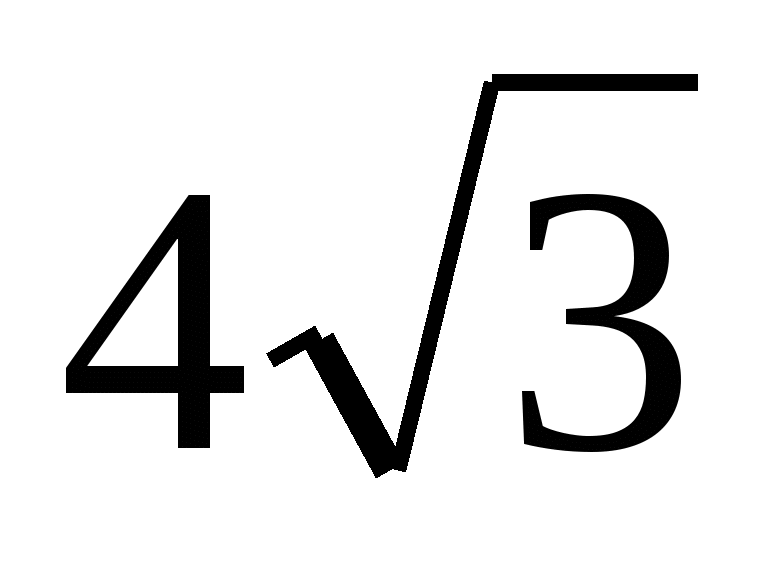 , A (
, A ( 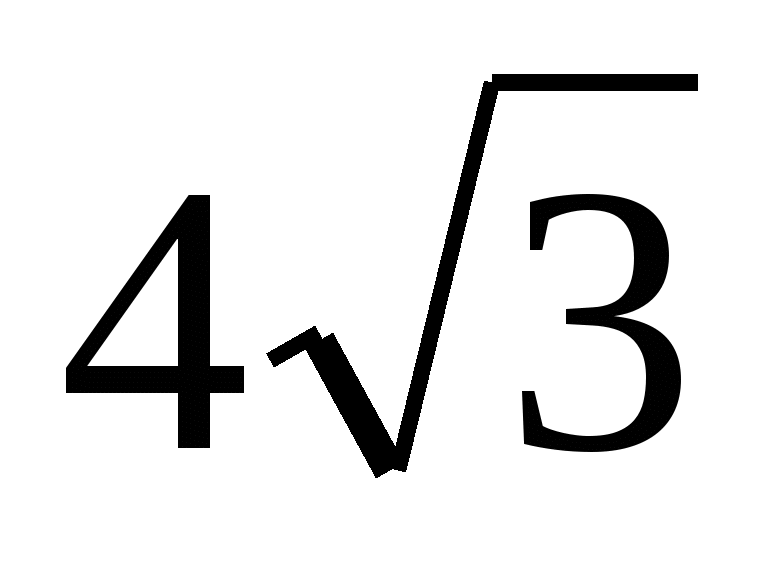 ;0;0)
;0;0)
B(  ; -2;0)
; -2;0)
F 1 ( 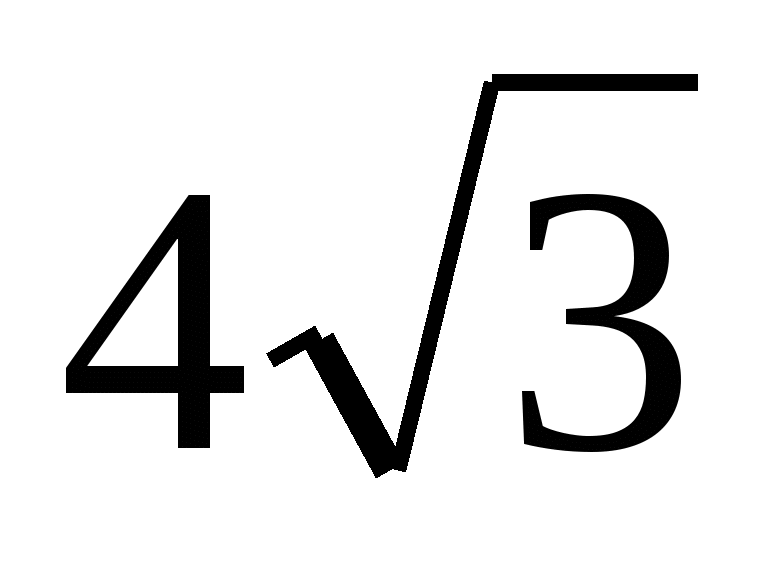 ;4;1)
;4;1)
E 1 (  ;6;1)
;6;1)
Let's write the coordinates of the direction vector for the straight line F 1E 1 (  ;-2;0), let F 1 (
;-2;0), let F 1 ( 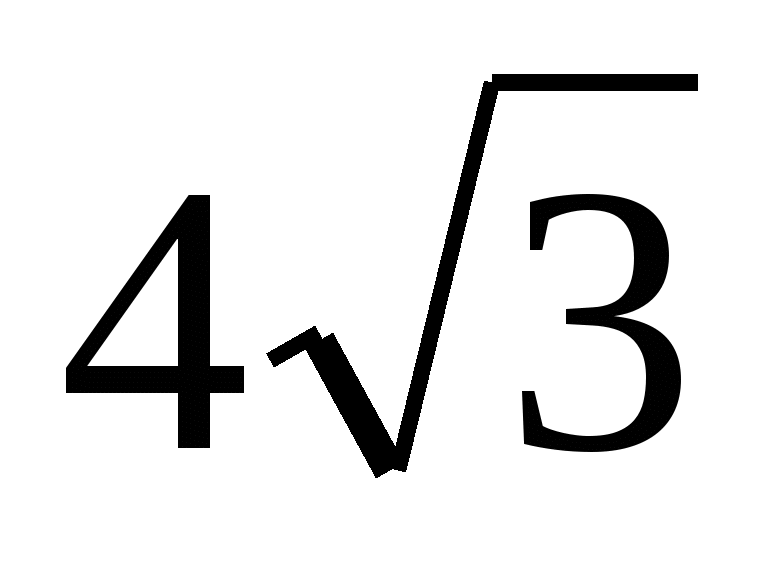 ;4;1) is a point on the line.
;4;1) is a point on the line.
Find the distance using the formula:
2 way:
Consider ∆BF 1E 1
BF1 = 
BE1= 
cosB=  ,
Then sinB=
,
Then sinB= 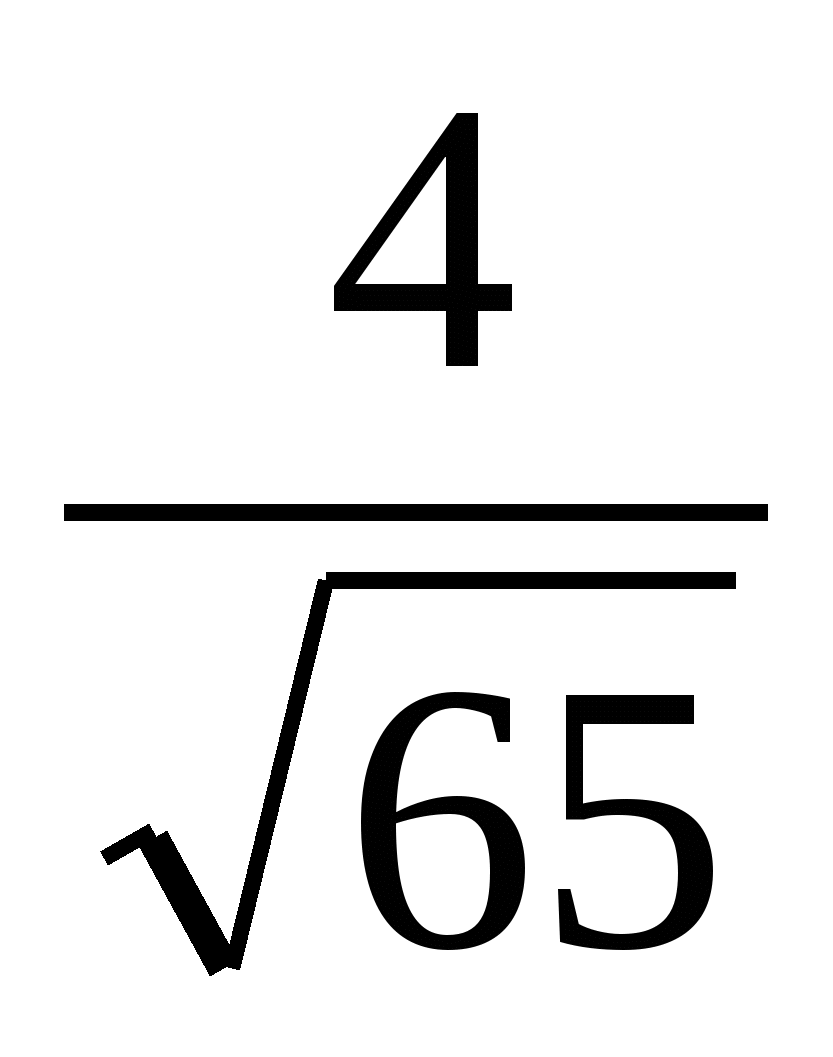
S ∆BF 1E 1=  , knowing the area ∆BF 1E 1 we find the height 14=1/2*4 *BH , where BH is the height drawn from the vertex B , i.e. distance from point B to line F 1E 1.
, knowing the area ∆BF 1E 1 we find the height 14=1/2*4 *BH , where BH is the height drawn from the vertex B , i.e. distance from point B to line F 1E 1.
BH=7
Tasks:
In a regular hexagonal prism ABCDEF A1B1C1D 1E 1F whose base sides are 4 and the side edges are 3, find the distance from point B to line C 1 D 1.
Answer: 
2. point to plane
Let it be necessary to find the distance from the point P (x 1; y 1; z 1) to the plane Ax + By + Cz + D \u003d 0, where (A; B; C) are the coordinates of the normal of the plane.
The formula for finding the distance between a point and a plane

Difficulty can arise when writing the equation of the plane.
Compilation of the plane equation is reduced to solving a system of three unknowns, consisting of equations obtained by substituting three points lying in the plane into the plane formula.
Example:
In a regular 3-sided pyramid, the side of the base is 12 cm. Find the distance from the center of the base to the side face if the dihedral angle at the edge of the base is π/3
H(  ; 6; 0)
; 6; 0)
B(0;12;0); C( 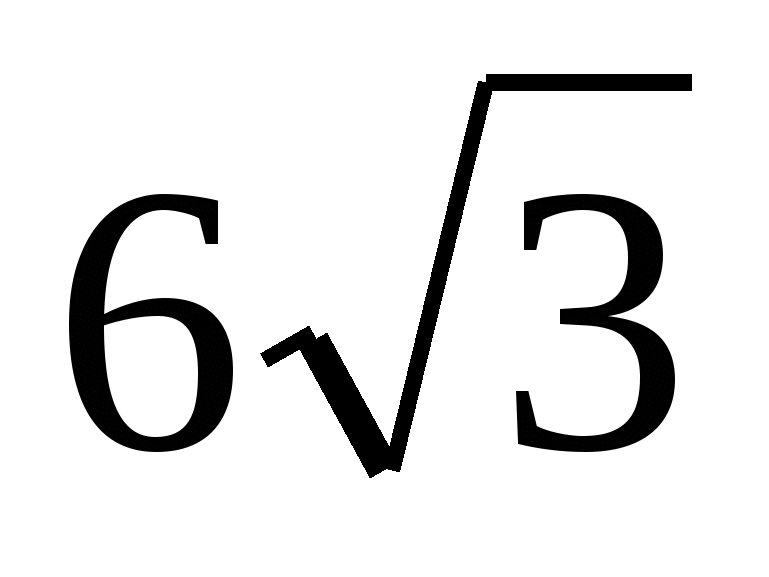 ;6;0); S(
;6;0); S(  ;6;6)
;6;6)
Let's write the equation of the plane:
B: 12V+D=0, then D=-12V
C: 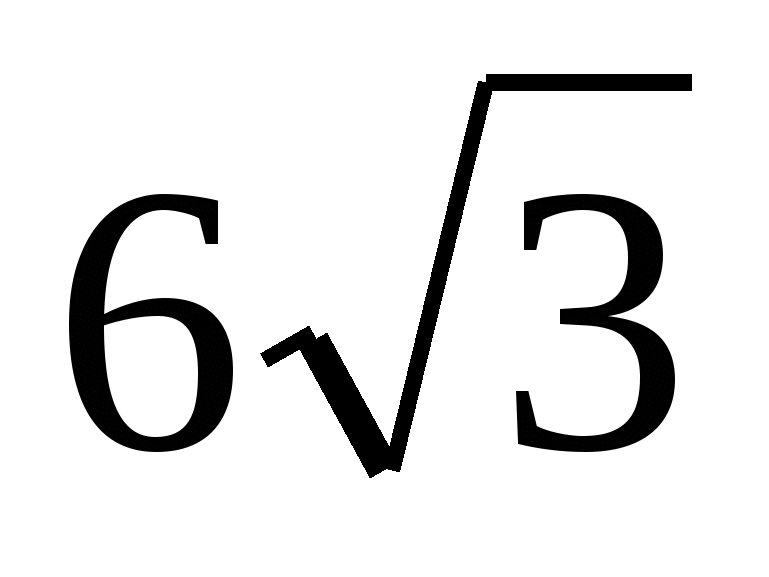 A+6B+D=0, A=
A+6B+D=0, A= 
S:  A+6B+6C+D=0; C=
A+6B+6C+D=0; C= 
Let's write the equation of the plane:

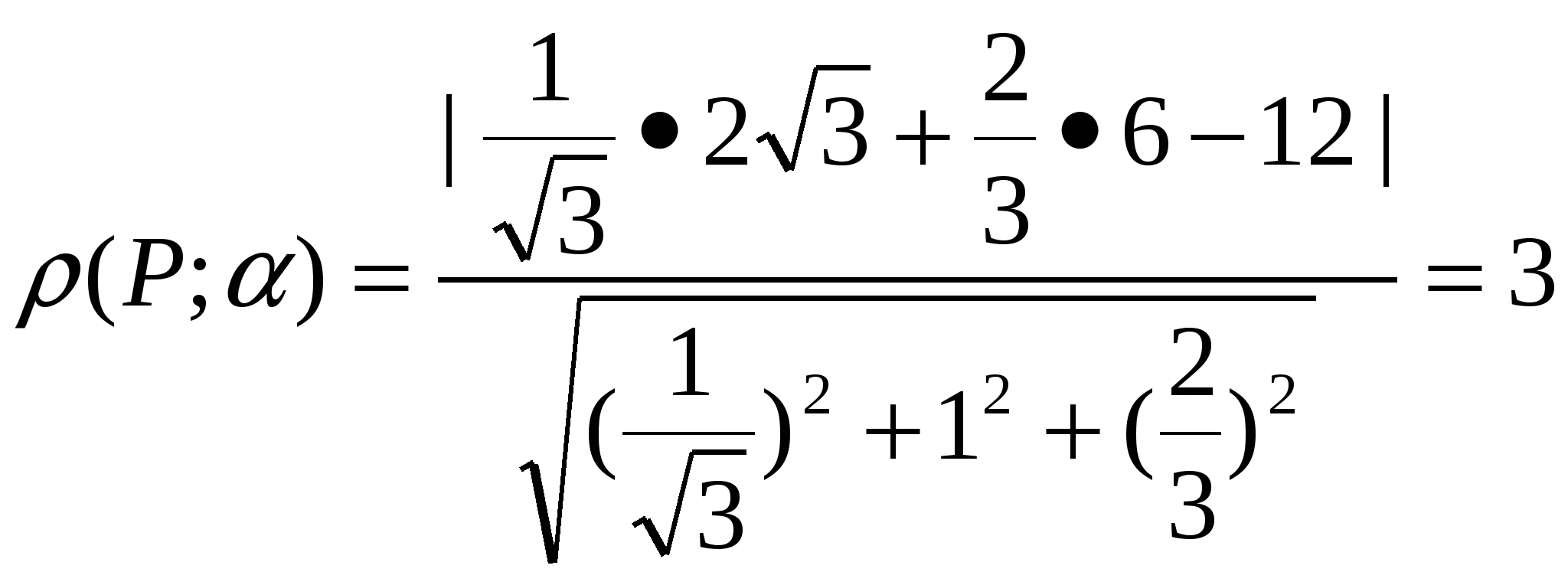 cm
cm
Answer: 3 cm
Tasks
The length of the edge of the cube AC 1 is equal to 1. Find the distance from the vertex B to the plane ASD 1
Answer: 
3. from a straight line to a plane and between planes
The solution of these problems is reduced to solving the problem of finding the distance from a point to a plane. It is necessary to take a point belonging to a straight line, and in the second case, a point belonging to one of the planes and thus find the distance from a point to a plane.
4. between crossing lines
The most common way to determine the distance between skew lines is to use the vector method. A vector is found that is equal in length to the common perpendicular to the skew lines and perpendicular to any non-zero vector located on each of these lines. Based on the equality to zero of the scalar product of two perpendicular vectors, we obtain a system of equations that allows us to determine the coordinates of the sought vector.
Given a unit cube ABCDA 1 B 1С1 D1 . Dot M - mid-rib BB 1 . Find distance between straight speakers 1 and DM .
Let the points R And Qare such that the segmentPQ - general perpendicular to intersecting direct AC1 And DM . Then PQ - a vector that is perpendicular vectors AC1 And DM Behind write the correct equation:
From it we get that PQ = MQ + BM + AB + P A

Vector  collinear vecto RU DM
,
i.e. there is such a numberA,
What
collinear vecto RU DM
,
i.e. there is such a numberA,
What  .
.
 (-1;1;1/2)
(-1;1;1/2)
Therefore, the vector MQ has coordinates ( a ;- a ;-1/2 a )
Vectors VM (0;0;1/2) And AB(0; 1; 0).
Vector AR collinear to the vector AC
1,
i.e., there is such number β,
What  and traceimportantly, vectorRA has coordinates (- β;-β;-β
).
Folding che tyre vector, we get that coordi natami vector PQ
there will be numbers
and traceimportantly, vectorRA has coordinates (- β;-β;-β
).
Folding che tyre vector, we get that coordi natami vector PQ
there will be numbers
(a -β;1-a -β;1/2-1/2a -β)
Quantities A And β define from the system:
 ;
; 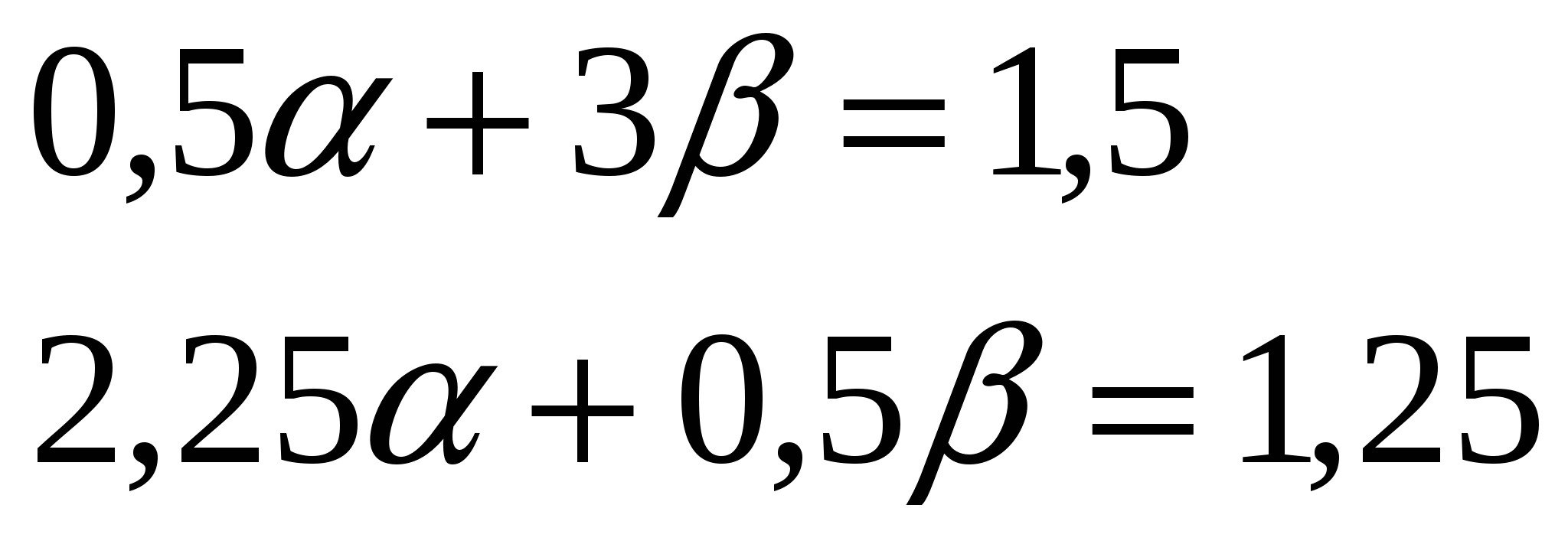 ;
; 
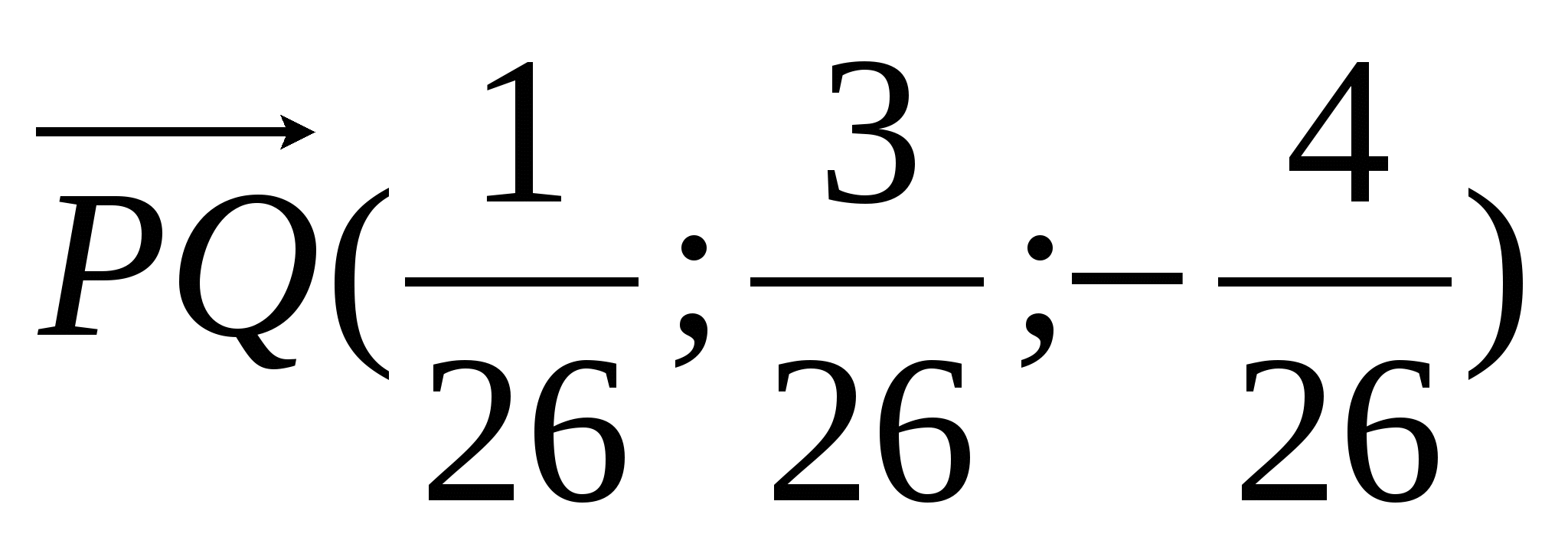
PQ= 
Answer: 
Tasks
In the pyramid D ABC, the lengths of the ribs AB = AC = D B = D C = 13cm, DA = 6cm, BC = 24cm are known. Find the distance between lines D A and BC.
Answer: 4cm
IN regular tetrahedron ABCD with edge equal to 1, point M - mid-rib sun, a dot N- middle AB. Find the distance between the lines CN And DM .
Answer: 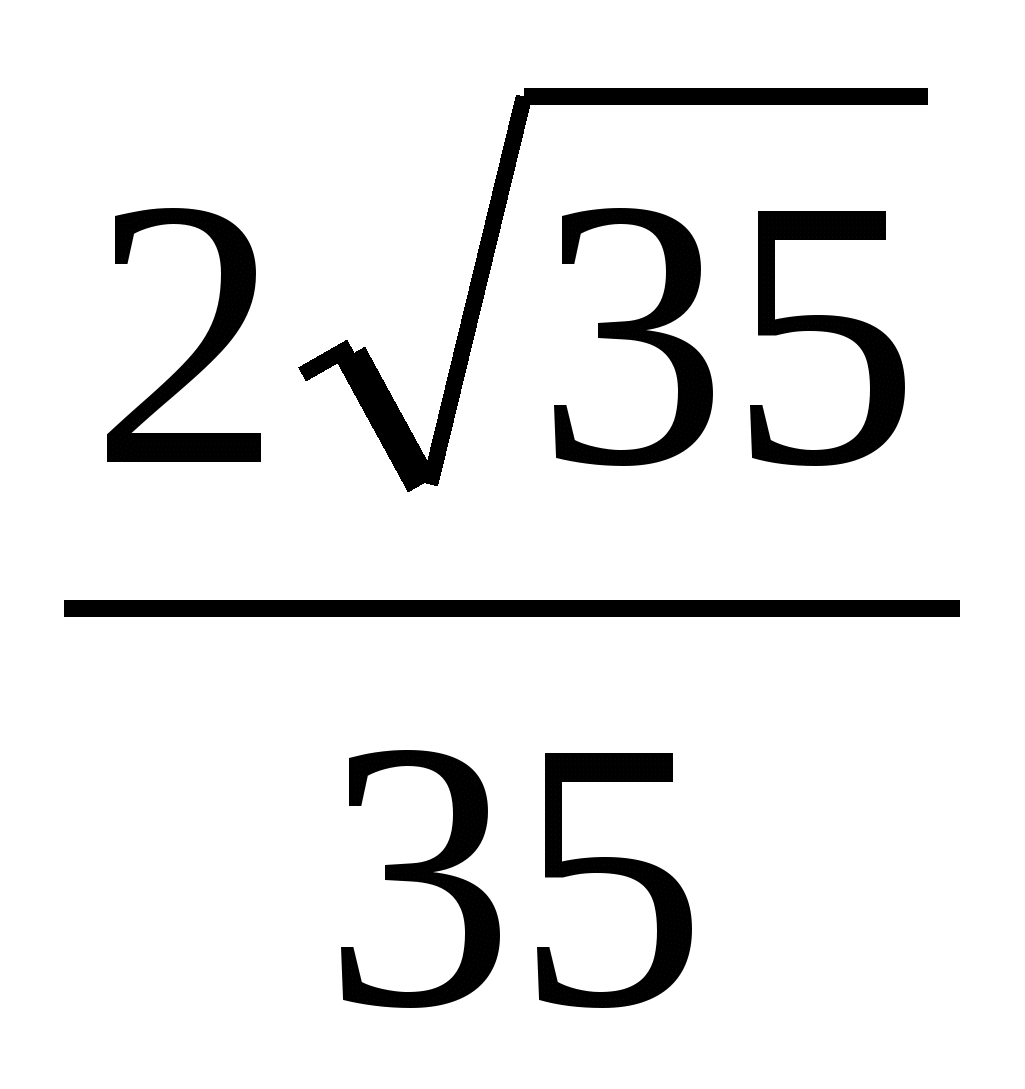
In a regular hexagonal prism ABCDEFA1B1C1D1E1F1, whose edges are equal to l, find the distance between the lines AB1 and BC1.
Answer; 
Finding corners
between straight lines
This task is reduced to finding the cosine of the angle between the direction vectors of these lines.
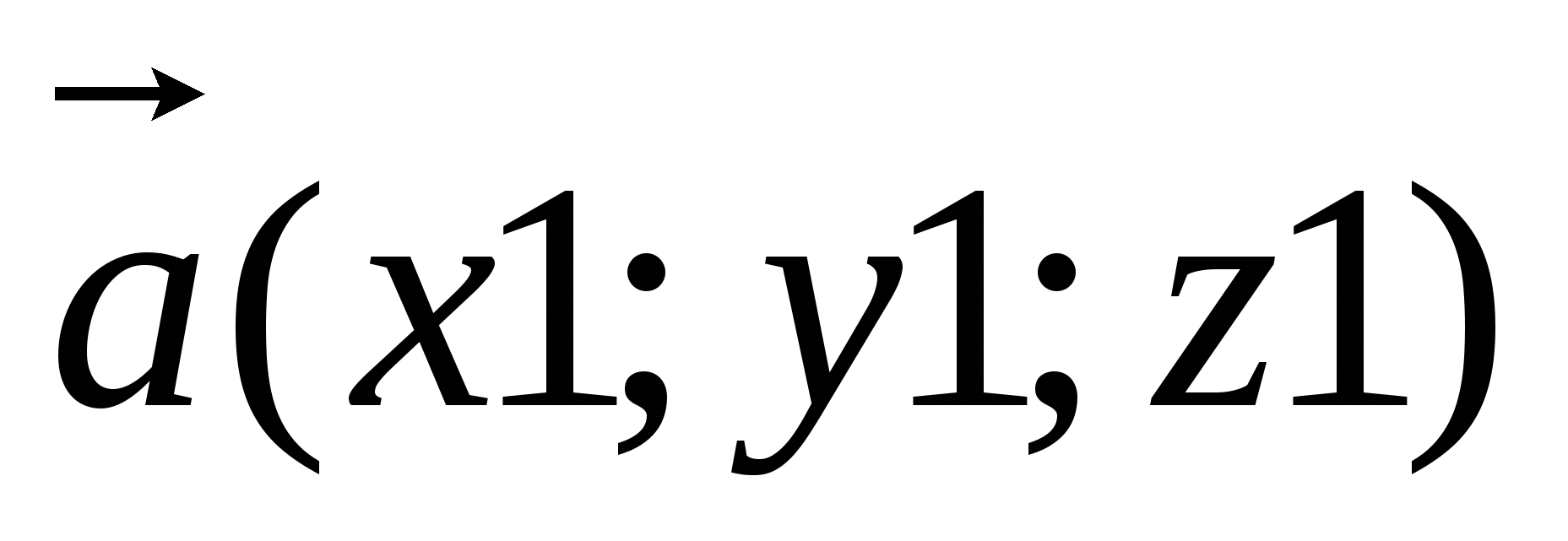
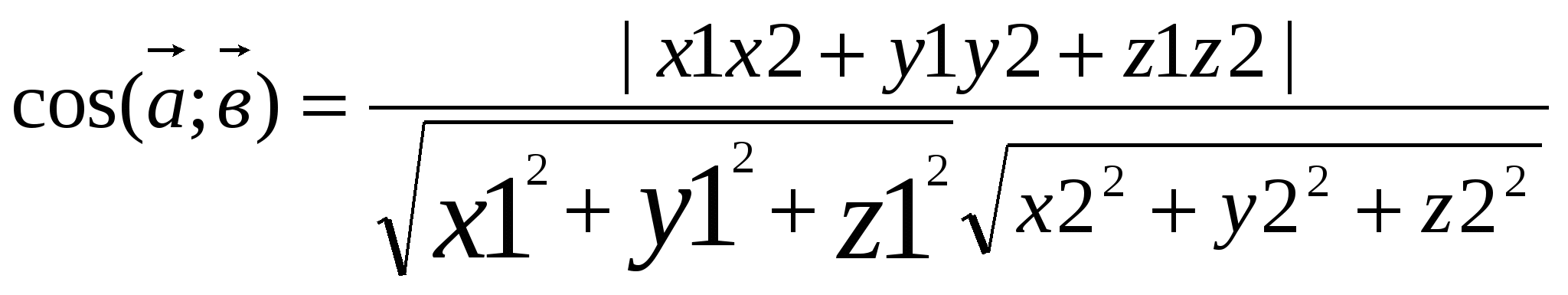
Task
In the cube ABCDA1B1C1D1 find the angle between lines AD1 and DE1 ,
where E is the midpoint of the edge CC1
D 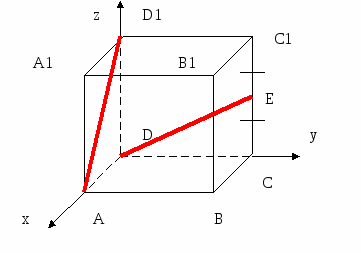 For definiteness, let's take the edge of the cube as 1.
For definiteness, let's take the edge of the cube as 1.



Tasks:
1. In the correct triangular prism ABCA1B1C1 , whose edges are equal to 1 , find the angle between lines AC1 and B1C
Answer: 
2. In a regular hexagonal pyramid MABCDEF with base sides equal to 1 and side edges equal to 2, find the cosine of the angle between MB and AD .
Answer: ¼
2. Between a straight line and a plane
This problem is reduced to finding the cosine of the angle between the normal to the plane and the directing vector of the straight line.
Ax + By + Cz + D \u003d 0, where (A; B; C) are the coordinates of the normal of the plane. a(x 1; y 1; z 1)
To find the coordinates of the normal, you need to write the equation of the plane using the known coordinates of three points (see the problem of finding the distance from a point to a plane)
|
 sin (flat; straight)=
sin (flat; straight)= 
Task: In a regular quadrangular pyramid MABCD , all edges of which are equal to 1, point E is the midpoint of edge MC. Find the sine of the angle between the line DE and the plane AMB.





