Pokud se budete řídit definicí, pak derivace funkce v bodě je limitou poměru přírůstku funkce Δ y na přírůstek argumentu Δ X:

Vše se zdá být jasné. Ale zkuste použít tento vzorec k výpočtu, řekněme, derivace funkce F(X) = X 2 + (2X+ 3) · E X hřích X. Pokud uděláte vše podle definice, pak po několika stránkách výpočtů jednoduše usnete. Proto existují jednodušší a efektivnější způsoby.

Nejprve si všimneme, že z celé řady funkcí můžeme rozlišit takzvané elementární funkce. Jedná se o poměrně jednoduché výrazy, jejichž derivace jsou již dávno vypočítány a tabelovány. Takové funkce jsou docela snadno zapamatovatelné - spolu s jejich deriváty.

Derivace elementárních funkcí

Elementární funkce jsou všechny ty, které jsou uvedeny níže. Deriváty těchto funkcí je třeba znát nazpaměť. Navíc není vůbec těžké si je zapamatovat - proto jsou elementární.

Takže derivace elementárních funkcí:

název	Funkce	Derivát
Konstantní	F(X) = C, C ∈ R	0 (ano, nula!)
Mocnina s racionálním exponentem	F(X) = X n	n · X n − 1
Sinus	F(X) = hřích X	cos X
Kosinus	F(X) = cos X	-hřích X(mínus sinus)
Tečna	F(X) = tg X	1/cos 2 X
Kotangens	F(X) = ctg X	− 1/hřích 2 X
Přirozený logaritmus	F(X) = log X	1/X
Libovolný logaritmus	F(X) = log A X	1/(X ln A)
Exponenciální funkce	F(X) = E X	E X(nic se nezměnilo)

Pokud se elementární funkce vynásobí libovolnou konstantou, pak se derivace nové funkce také snadno vypočítá:

(C · F)’ = C · F ’.

Obecně lze konstanty vyjmout ze znaménka derivace. Například:

(2X 3)‘ = 2 · ( X 3) = 2 3 X 2 = 6X 2 .

Je zřejmé, že elementární funkce lze vzájemně sčítat, násobit, dělit – a mnoho dalšího. Tak se objeví nové funkce, již ne nijak zvlášť elementární, ale také diferencované podle určitých pravidel. Tato pravidla jsou popsána níže.

Derivace součtu a rozdílu

Nechť jsou dány funkce F(X) A G(X), jejichž deriváty jsou nám známé. Můžete si například vzít výše popsané základní funkce. Pak můžete najít derivaci součtu a rozdílu těchto funkcí:

1. (F + G)’ = F ’ + G ’
2. (F − G)’ = F ’ − G ’

Takže derivace součtu (rozdílu) dvou funkcí se rovná součtu (rozdílu) derivací. Termínů může být více. Například, ( F + G + h)’ = F ’ + G ’ + h ’.

Přísně vzato, v algebře neexistuje pojem „odčítání“. Existuje koncept „negativního prvku“. Proto ten rozdíl F − G lze přepsat jako součet F+ (-1) G, a pak zbývá pouze jeden vzorec - derivace součtu.

F(X) = X 2 + sin x; G(X) = X 4 + 2X 2 − 3.

Funkce F(X) je součet dvou elementárních funkcí, tedy:

F ’(X) = (X 2 + hřích X)’ = (X 2) + (hřích X)’ = 2X+ cos x;

Podobně uvažujeme i u funkce G(X). Pouze již existují tři termíny (z hlediska algebry):

G ’(X) = (X 4 + 2X 2 − 3)’ = (X 4 + 2X 2 + (−3))’ = (X 4)’ + (2X 2)’ + (−3)’ = 4X 3 + 4X + 0 = 4X · ( X 2 + 1).

Odpovědět:
F ’(X) = 2X+ cos x;
G ’(X) = 4X · ( X 2 + 1).

Derivát produktu

Matematika je logická věda, takže mnoho lidí věří, že pokud se derivace součtu rovná součtu derivací, pak derivace součinu stávkovat">rovná se součinu derivátů. Ale vykašli se na to! Derivát součinu se vypočítá podle úplně jiného vzorce. Konkrétně:

(F · G) ’ = F ’ · G + F · G ’

Vzorec je jednoduchý, ale často se na něj zapomíná. A to nejen školáků, ale i studentů. Výsledkem jsou nesprávně vyřešené problémy.

Úkol. Najděte derivace funkcí: F(X) = X 3 cos x; G(X) = (X 2 + 7X− 7) · E X .

Funkce F(X) je součin dvou elementárních funkcí, takže vše je jednoduché:

F ’(X) = (X 3 cos X)’ = (X 3)' cos X + X 3 (cos X)’ = 3X 2 cos X + X 3 (- hřích X) = X 2 (3 cos X − X hřích X)

Funkce G(X) první násobitel je trochu složitější, ale obecné schéma se nemění. Je zřejmé, že první faktor funkce G(X) je polynom a jeho derivace je derivací součtu. My máme:

G ’(X) = ((X 2 + 7X− 7) · E X)’ = (X 2 + 7X− 7)' · E X + (X 2 + 7X− 7) · ( E X)’ = (2X+ 7) · E X + (X 2 + 7X− 7) · E X = E X· (2 X + 7 + X 2 + 7X −7) = (X 2 + 9X) · E X = X(X+ 9) · E X .

Odpovědět:
F ’(X) = X 2 (3 cos X − X hřích X);
G ’(X) = X(X+ 9) · E X .

Upozorňujeme, že v posledním kroku je derivace faktorizována. Formálně to není potřeba dělat, ale většina derivací se nepočítá sama o sobě, ale pro zkoumání funkce. To znamená, že se derivace bude dále rovnat nule, určí se její znaménka a tak dále. Pro takový případ je lepší mít výraz faktorizovaný.

Pokud existují dvě funkce F(X) A G(X), a G(X) ≠ 0 na množině, která nás zajímá, můžeme definovat novou funkci h(X) = F(X)/G(X). Pro takovou funkci můžete také najít derivaci:

Není slabý, co? Kde se vzalo mínus? Proč G 2? A takhle! Toto je jeden z nejsložitějších vzorců - bez láhve na to nepřijdete. Proto je lepší si to prostudovat na konkrétních příkladech.

Úkol. Najděte derivace funkcí:

Čitatel a jmenovatel každého zlomku obsahuje elementární funkce, takže vše, co potřebujeme, je vzorec pro derivaci podílu:

Podle tradice rozložme čitatel na faktor – tím se značně zjednoduší odpověď:

Komplexní funkce nemusí být nutně půlkilometrový vzorec. Například stačí vzít funkci F(X) = hřích X a nahradit proměnnou Xřekněme dál X 2 + ln X. ono to vyjde F(X) = hřích ( X 2 + ln X) - jedná se o komplexní funkci. Má také odvozeninu, ale nebude možné ji najít pomocí výše uvedených pravidel.

Co bych měl dělat? V takových případech pomůže nahrazení proměnné a vzorce za derivaci komplexní funkce:

F ’(X) = F ’(t) · t', Pokud X je nahrazeno t(X).

Situace s pochopením tohoto vzorce je zpravidla ještě smutnější než s derivací kvocientu. Proto je také lepší to vysvětlit na konkrétních příkladech, s podrobným popisem každého kroku.

Úkol. Najděte derivace funkcí: F(X) = E 2X + 3 ; G(X) = hřích ( X 2 + ln X)

Všimněte si, že pokud ve funkci F(X) místo výrazu 2 X+ 3 bude snadné X, pak dostaneme elementární funkci F(X) = E X. Proto provedeme náhradu: nechť 2 X + 3 = t, F(X) = F(t) = E t. Hledáme derivaci komplexní funkce pomocí vzorce:

F ’(X) = F ’(t) · t ’ = (E t)’ · t ’ = E t · t ’

A teď - pozor! Provádíme zpětnou výměnu: t = 2X+ 3. Dostáváme:

F ’(X) = E t · t ’ = E 2X+ 3 (2 X + 3)’ = E 2X+ 3 2 = 2 E 2X + 3

Nyní se podíváme na funkci G(X). Je zřejmé, že je třeba jej vyměnit X 2 + ln X = t. My máme:

G ’(X) = G ’(t) · t‘ = (hřích t)’ · t’ = cos t · t ’

Reverzní výměna: t = X 2 + ln X. Pak:

G ’(X) = cos ( X 2 + ln X) · ( X 2 + ln X)‘ = cos ( X 2 + ln X) · (2 X + 1/X).

To je vše! Jak je vidět z posledního výrazu, celý problém se zredukoval na výpočet derivačního součtu.

Odpovědět:
F ’(X) = 2 · E 2X + 3 ;
G ’(X) = (2X + 1/X) cos ( X 2 + ln X).

Velmi často ve svých lekcích místo termínu „derivát“ používám slovo „první“. Například zdvih součtu se rovná součtu zdvihů. Je to jasnější? Dobře, to je super.

Výpočet derivace tedy spočívá v zbavení se stejných tahů podle výše uvedených pravidel. Jako poslední příklad se vraťme k derivační mocnině s racionálním exponentem:

(X n)’ = n · X n − 1

To v roli málokdo ví n může být i zlomkové číslo. Například kořen je X 0,5. Co když je pod kořenem něco fantastického? Opět bude výsledkem komplexní funkce – takové konstrukce rádi dávají v testech a zkouškách.

Úkol. Najděte derivaci funkce:

Nejprve přepišme odmocninu jako mocninu s racionálním exponentem:

F(X) = (X 2 + 8X − 7) 0,5 .

Nyní uděláme náhradu: let X 2 + 8X − 7 = t. Derivaci najdeme pomocí vzorce:

F ’(X) = F ’(t) · t ’ = (t 0,5)' · t’ = 0,5 · t−0,5 · t ’.

Udělejme obrácenou výměnu: t = X 2 + 8X− 7. Máme:

F ’(X) = 0,5 · ( X 2 + 8X− 7) −0,5 · ( X 2 + 8X− 7)’ = 0,5 · (2 X+ 8) ( X 2 + 8X − 7) −0,5 .

Nakonec zpět ke kořenům:

Operace hledání derivace se nazývá diferenciace.

V důsledku řešení problémů hledání derivací nejjednodušších (a nepříliš jednoduchých) funkcí definováním derivace jako limity poměru přírůstku k přírůstku argumentu se objevila tabulka derivací a přesně definovaná pravidla derivace. . První, kdo pracoval v oblasti hledání derivátů, byli Isaac Newton (1643-1727) a Gottfried Wilhelm Leibniz (1646-1716).

Proto v naší době, abychom našli derivaci libovolné funkce, nepotřebujeme vypočítat výše zmíněnou mez poměru přírůstku funkce k přírůstku argumentu, ale stačí použít tabulku derivace a pravidla diferenciace. Pro nalezení derivace je vhodný následující algoritmus.

Chcete-li najít derivát, potřebujete výraz pod prvočíslem rozdělit jednoduché funkce na komponenty a určit, jaké akce (součin, součet, podíl) tyto funkce spolu souvisí. Dále najdeme derivace elementárních funkcí v tabulce derivací a vzorce pro derivace součinu, součtu a kvocientu - v pravidlech derivování. Tabulka derivací a pravidla diferenciace jsou uvedeny po prvních dvou příkladech.

Příklad 1. Najděte derivaci funkce

Řešení. Z pravidel derivace zjistíme, že derivace součtu funkcí je součtem derivací funkcí, tzn.

Z tabulky derivací zjistíme, že derivace "x" je rovna jedné a derivace sinu je rovna kosinu. Tyto hodnoty dosadíme do součtu derivací a najdeme derivaci požadovanou podmínkou problému:

Příklad 2 Najděte derivaci funkce

Řešení. Derivujeme jako derivaci součtu, ve kterém má druhý člen konstantní faktor; lze jej vyjmout ze znaménka derivace:

Pokud stále vyvstávají otázky o tom, odkud něco pochází, jsou obvykle vyjasněny poté, co se seznámíte s tabulkou derivací a nejjednoduššími pravidly diferenciace. Právě k nim přecházíme.

Tabulka derivací jednoduchých funkcí

1. Derivace konstanty (čísla). Jakékoli číslo (1, 2, 5, 200...), které je ve výrazu funkce. Vždy se rovná nule. To je velmi důležité mít na paměti, protože je to velmi často vyžadováno
2. Derivace nezávisle proměnné. Nejčastěji "X". Vždy se rovná jedné. To je také důležité si dlouho pamatovat
3. Derivace stupně. Při řešení problémů je potřeba převést neodmocniny na mocniny.
4. Derivace proměnné k mocnině -1
5. Derivace odmocniny
6. Derivace sinusu
7. Derivace kosinusu
8. Derivace tečny
9. Derivace kotangens
10. Derivace arcsinusu
11. Derivát arkosinu
12. Derivace arkustangens
13. Derivace obloukového kotangens
14. Derivace přirozeného logaritmu
15. Derivace logaritmické funkce
16. Derivace exponentu
17. Derivace exponenciální funkce

Pravidla diferenciace

1. Derivace součtu nebo rozdílu
2. Derivát produktu
2a. Derivace výrazu násobená konstantním faktorem
3. Derivace kvocientu
4. Derivace komplexní funkce

Pravidlo 1.Pokud funkce

jsou v určitém bodě diferencovatelné, pak jsou funkce diferencovatelné ve stejném bodě

a

těch. derivace algebraického součtu funkcí se rovná algebraickému součtu derivací těchto funkcí.

Následek. Pokud se dvě diferencovatelné funkce liší konstantním členem, pak jsou jejich derivace stejné, tj.

Pravidlo 2.Pokud funkce

jsou v určitém bodě diferencovatelné, pak je jejich produkt diferencovatelný ve stejném bodě

a

těch. Derivace součinu dvou funkcí se rovná součtu součinů každé z těchto funkcí a derivace druhé.

Důsledek 1. Konstantní faktor lze vyjmout ze znaménka derivace:

Důsledek 2. Derivace součinu několika diferencovatelných funkcí se rovná součtu součinů derivace každého faktoru a všech ostatních.

Například pro tři násobiče:

Pravidlo 3.Pokud funkce

v určitém okamžiku rozlišitelné A , pak v tomto bodě je jejich kvocient také diferencovatelnýu/v a

těch. derivace podílu dvou funkcí se rovná zlomku, jehož čitatel je rozdílem součinů jmenovatele a derivace v čitateli a čitatele a derivace jmenovatele, a jmenovatel je druhá mocnina bývalý čitatel.

Kde hledat věci na jiných stránkách

Při hledání derivace součinu a kvocientu v reálných problémech je vždy nutné aplikovat více diferenciačních pravidel najednou, proto je v článku více příkladů na tyto derivace"Derivace produktu a kvocient funkcí".

Komentář. Neměli byste zaměňovat konstantu (tedy číslo) jako člen v součtu a jako konstantní faktor! V případě členu je jeho derivace rovna nule a v případě konstantního faktoru je vyjmuta ze znaménka derivací. Toto je typická chyba, která se vyskytuje v počáteční fázi studia odvozenin, ale protože průměrný student řeší několik jedno- a dvoudílných příkladů, již tuto chybu nedělá.

A pokud při rozlišování produktu nebo kvocientu máte termín u"proti, ve kterém u- číslo, například 2 nebo 5, tedy konstanta, pak bude derivace tohoto čísla rovna nule, a tedy celý člen bude roven nule (tento případ je probrán v příkladu 10).

Další častou chybou je mechanické řešení derivace komplexní funkce jako derivace jednoduché funkce. Proto derivace komplexní funkce je věnován samostatný článek. Nejprve se ale naučíme najít derivace jednoduchých funkcí.

Po cestě se neobejdete bez transformace výrazů. Chcete-li to provést, možná budete muset otevřít příručku v nových oknech. Akce se silami a kořeny A Operace se zlomky .

Pokud hledáte řešení pro derivace zlomků s mocninou a odmocninou, tedy když funkce vypadá a poté postupujte podle lekce „Derivace součtů zlomků s mocninami a odmocninami“.

Pokud máte úkol jako , poté absolvujete lekci „Derivace jednoduchých goniometrických funkcí“.

Příklady krok za krokem - jak najít derivaci

Příklad 3 Najděte derivaci funkce

Řešení. Definujeme části funkčního výrazu: celý výraz představuje součin a jeho činitele jsou součty, ve druhém z nich jeden z členů obsahuje konstantní činitel. Aplikujeme pravidlo diferenciace součinu: derivace součinu dvou funkcí se rovná součtu součinů každé z těchto funkcí derivací druhé:

Dále použijeme pravidlo derivace součtu: derivace algebraického součtu funkcí se rovná algebraickému součtu derivací těchto funkcí. V našem případě má v každém součtu druhý člen znaménko mínus. V každém součtu vidíme jak nezávislou proměnnou, jejíž derivace je rovna jedné, tak konstantu (číslo), jejíž derivace je rovna nule. Takže „X“ se změní na jedničku a mínus 5 na nulu. Ve druhém výrazu je "x" násobeno 2, takže násobíme dva stejnou jednotkou jako derivace "x". Získáme následující derivační hodnoty:

Nalezené derivace dosadíme do součtu součinů a získáme derivaci celé funkce, kterou vyžaduje podmínka problému:

A můžete zkontrolovat řešení problému s derivací na.

Příklad 4. Najděte derivaci funkce

Řešení. Musíme najít derivaci kvocientu. Aplikujeme vzorec pro derivování kvocientu: derivace kvocientu dvou funkcí se rovná zlomku, jehož čitatel je rozdílem součinů jmenovatele a derivace čitatele a čitatele a derivace jmenovatel a jmenovatel je druhá mocnina dřívějšího čitatele. Dostaneme:

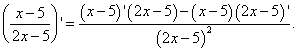
Derivaci faktorů v čitateli jsme již našli v příkladu 2. Nezapomeňme také, že součin, který je v aktuálním příkladu druhým faktorem v čitateli, je brán se znaménkem mínus:

Pokud hledáte řešení problémů, ve kterých potřebujete najít derivaci funkce, kde je souvislá hromada odmocnin a mocnin, jako je např. , pak vítejte ve třídě "Derivace součtů zlomků s mocninou a odmocninou" .

Pokud se potřebujete dozvědět více o derivacích sinů, kosinů, tečen a dalších goniometrických funkcí, tedy když funkce vypadá , pak lekce pro vás "Derivace jednoduchých goniometrických funkcí" .

Příklad 5. Najděte derivaci funkce

Řešení. V této funkci vidíme součin, jehož jedním z faktorů je odmocnina nezávisle proměnné, s jejíž derivací jsme se seznámili v tabulce derivací. Pomocí pravidla pro derivování součinu a tabulkové hodnoty derivace odmocniny získáme:

Řešení problému s derivací můžete zkontrolovat na online kalkulačka derivátů .

Příklad 6. Najděte derivaci funkce

Řešení. V této funkci vidíme kvocient, jehož dividenda je druhou odmocninou nezávislé proměnné. Pomocí pravidla derivace kvocientů, které jsme zopakovali a použili v příkladu 4, a tabulkové hodnoty derivace odmocniny, získáme:

Chcete-li se zbavit zlomku v čitateli, vynásobte čitatel a jmenovatel číslem .

A věta o derivaci komplexní funkce, jejíž formulace je následující:

Nechť 1) funkce $u=\varphi (x)$ má v určitém bodě $x_0$ derivaci $u_(x)"=\varphi"(x_0)$, 2) funkce $y=f(u)$ mít v odpovídajícím bodě $u_0=\varphi (x_0)$ derivaci $y_(u)"=f"(u)$. Pak bude mít i komplexní funkce $y=f\left(\varphi (x) \right)$ ve zmíněném bodě derivaci rovnou součinu derivací funkcí $f(u)$ a $\varphi ( x) $:

$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \right)\cdot \varphi"(x_0) $$

nebo v kratším zápisu: $y_(x)"=y_(u)"\cdot u_(x)"$.

V příkladech v této části mají všechny funkce tvar $y=f(x)$ (tj. uvažujeme pouze funkce jedné proměnné $x$). V souladu s tím je ve všech příkladech derivace $y"$ brána vzhledem k proměnné $x$. Abychom zdůraznili, že derivace je brána vzhledem k proměnné $x$, místo $y se často píše $y"_x$ "$.

Příklady č. 1, č. 2 a č. 3 nastiňují podrobný postup hledání derivace komplexních funkcí. Příklad č. 4 je určen pro úplnější pochopení derivační tabulky a má smysl se s ní seznámit.

Je vhodné po prostudování látky v příkladech č. 1-3 přejít k samostatnému řešení příkladů č. 5, č. 6 a č. 7. Příklady #5, #6 a #7 obsahují krátké řešení, aby si čtenář mohl zkontrolovat správnost svého výsledku.

Příklad č. 1

Najděte derivaci funkce $y=e^(\cos x)$.

Potřebujeme najít derivaci komplexní funkce $y"$. Protože $y=e^(\cos x)$, pak $y"=\left(e^(\cos x)\right)"$. Chcete-li najděte derivaci $ \left(e^(\cos x)\right)"$ použijeme vzorec č. 6 z tabulky derivací. Abychom mohli použít vzorec č. 6, musíme vzít v úvahu, že v našem případě $u=\cos x$. Další řešení spočívá v jednoduchém dosazení výrazu $\cos x$ místo $u$ do vzorce č. 6:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$

Nyní potřebujeme najít hodnotu výrazu $(\cos x)"$. Znovu se vrátíme k tabulce derivací a vybereme z ní vzorec č. 10. Dosazením $u=x$ do vzorce č. 10 máme : $(\cos x)"=-\ sin x\cdot x"$. Nyní pokračujeme v rovnosti (1.1) a doplníme ji o nalezený výsledek:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \tag (1.2) $$

Protože $x"=1$, pokračujeme v rovnosti (1.2):

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$

Z rovnosti (1.3) tedy máme: $y"=-\sin x\cdot e^(\cos x)$. Vysvětlení a mezilehlé rovnosti se samozřejmě obvykle přeskakují a zjištění derivace se zapíše na jeden řádek, jako v rovnosti ( 1.3) Takže derivace komplexní funkce byla nalezena, zbývá jen zapsat odpověď.

Odpovědět: $y"=-\sin x\cdot e^(\cos x)$.

Příklad č. 2

Najděte derivaci funkce $y=9\cdot \arctg^(12)(4\cdot \ln x)$.

Musíme vypočítat derivaci $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$. Nejprve si všimneme, že konstantu (tj. číslo 9) lze vyjmout z derivačního znaménka:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$

Nyní přejdeme k výrazu $\left(\arctg^(12)(4\cdot \ln x) \right)"$. Abychom usnadnili výběr požadovaného vzorce z tabulky derivací, uvedu výraz dotyčný v tomto tvaru: $\left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. Nyní je jasné, že je nutné použít vzorec č. 2, tzn. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Dosadíme $u=\arctg(4\cdot \ln x)$ a $\alpha=12$ do tohoto vzorce:

Doplněním rovnosti (2.1) k získanému výsledku máme:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“ \tag (2.2) $$

V této situaci se často udělá chyba, když řešitel v prvním kroku zvolí místo vzorce vzorec $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ $\left(u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Jde o to, že derivace externí funkce musí být na prvním místě. Abyste pochopili, která funkce bude externí vůči výrazu $\arctg^(12)(4\cdot 5^x)$, představte si, že počítáte hodnotu výrazu $\arctg^(12)(4\cdot 5^ x)$ v nějaké hodnotě $x$. Nejprve vypočítáte hodnotu $5^x$, poté výsledek vynásobíte 4, dostanete $4\cdot 5^x$. Nyní z tohoto výsledku vezmeme arkustangens a získáme $\arctg(4\cdot 5^x)$. Potom výsledné číslo zvýšíme na dvanáctou mocninu, dostaneme $\arctg^(12)(4\cdot 5^x)$. Poslední akce, tzn. zvýšení na 12 bude externí funkcí. A právě od toho musíme začít hledat derivaci, což bylo provedeno v rovnosti (2.2).

Nyní potřebujeme najít $(\arctg(4\cdot \ln x))"$. Použijeme vzorec č. 19 z tabulky derivací, do kterého dosadíme $u=4\cdot \ln x$:

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$

Výsledný výraz trochu zjednodušíme a vezmeme v úvahu $(4\cdot \ln x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$.

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$

Rovnost (2.2) se nyní stane:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \tag (2.3) $$

Zbývá najít $(4\cdot \ln x)"$. Vezmeme konstantu (tj. 4) z derivačního znaménka: $(4\cdot \ln x)"=4\cdot (\ln x)" $. Pro Abychom našli $(\ln x)"$, použijeme vzorec č. 8, do kterého dosadíme $u=x$: $(\ln x)"=\frac(1)(x)\cdot x "$. Protože $x"=1$, pak $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $ Dosazením získaného výsledku do vzorce (2.3) získáme:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).$ $

Připomínám, že derivace komplexní funkce se nejčastěji nachází na jednom řádku, jak je napsáno v poslední rovnosti. Proto při přípravě standardních výpočtů nebo kontrolních prací není vůbec nutné řešení tak podrobně popisovat.

Odpovědět: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.

Příklad č. 3

Najděte $y"$ funkce $y=\sqrt(\sin^3(5\cdot9^x))$.

Nejprve mírně transformujme funkci $y$, vyjádříme radikál (kořen) jako mocninu: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\cdot 9) ^x) \right)^(\frac(3)(7))$. Nyní začneme hledat derivaci. Protože $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$, pak:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \tag (3.1) $$

Použijme vzorec č. 2 z tabulky derivací, do kterého dosadíme $u=\sin(5\cdot 9^x)$ a $\alpha=\frac(3)(7)$:

$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$

Pokračujme v rovnosti (3.1) s použitím získaného výsledku:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$

Nyní potřebujeme najít $(\sin(5\cdot 9^x))"$. K tomu použijeme vzorec č. 9 z tabulky derivací, do kterého dosadíme $u=5\cdot 9^x$:

$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$

Po doplnění rovnosti (3.2) získaným výsledkem máme:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)" \tag (3.3) $$

Zbývá najít $(5\cdot 9^x)"$. Nejprve vezměme konstantu (číslo $5$) mimo derivační znaménko, tj. $(5\cdot 9^x)"=5\cdot (9 ^x) "$. Chcete-li najít derivaci $(9^x)"$, použijte vzorec č. 5 z tabulky derivací a dosaďte do něj $a=9$ a $u=x$: $(9^x )"=9^x\cdot \ ln9\cdot x"$. Protože $x"=1$, pak $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. Nyní můžeme pokračovat v rovnosti (3.3):

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$

Můžeme se opět vrátit od mocnin k radikálům (tj. kořenům) zapsáním $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ ve tvaru $\ frac(1)(\left(\sin(5\cdot 9^x)\right)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\) cdot 9^x)))$. Poté bude derivace zapsána v tomto tvaru:

$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$

Odpovědět: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\) cdot 9^x)))$.

Příklad č. 4

Ukažte, že vzorce č. 3 a č. 4 tabulky derivací jsou speciálním případem vzorce č. 2 této tabulky.

Vzorec č. 2 tabulky derivací obsahuje derivaci funkce $u^\alpha$. Dosazením $\alpha=-1$ do vzorce č. 2 dostaneme:

$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$

Protože $u^(-1)=\frac(1)(u)$ a $u^(-2)=\frac(1)(u^2)$, lze rovnost (4.1) přepsat následovně: $ \left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. Toto je vzorec č. 3 tabulky derivátů.

Vraťme se znovu ke vzorci č. 2 tabulky derivací. Dosadíme do něj $\alpha=\frac(1)(2)$:

$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$

Protože $u^(\frac(1)(2))=\sqrt(u)$ a $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, pak rovnost (4.2) lze přepsat následovně:

$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$

Výsledná rovnost $(\sqrt(u))"=\frac(1)(2\sqrt(u))\cdot u"$ je vzorec č. 4 tabulky derivací. Jak vidíte, vzorce č. 3 a č. 4 tabulky derivací se získají ze vzorce č. 2 dosazením odpovídající hodnoty $\alpha$.

Na kterém jsme zkoumali nejjednodušší derivace, a také se seznámili s pravidly diferenciace a některými technickými technikami hledání derivací. Pokud tedy nejste s derivacemi funkcí příliš zběhlí nebo vám některé body v tomto článku nejsou zcela jasné, přečtěte si nejprve výše uvedenou lekci. Prosím o vážnou náladu - materiál není jednoduchý, ale přesto se jej pokusím podat jednoduše a srozumitelně.

V praxi se musíte s derivací komplexní funkce vypořádat velmi často, dokonce bych řekl, že téměř vždy, když dostanete úkoly na hledání derivací.

Podíváme se do tabulky na pravidlo (č. 5) pro derivování komplexní funkce:

Pojďme na to přijít. V první řadě si dejte pozor na zadání. Zde máme dvě funkce - a , přičemž funkce je, obrazně řečeno, vnořena do funkce . Funkce tohoto typu (když je jedna funkce vnořena do jiné) se nazývá komplexní funkce.

Zavolám funkci vnější funkce a funkce – vnitřní (nebo vnořená) funkce.

! Tyto definice nejsou teoretické a neměly by se objevit v konečném návrhu zadání. Neformální výrazy „externí funkce“, „interní“ funkce používám pouze proto, abych vám usnadnil pochopení látky.

Chcete-li objasnit situaci, zvažte:

Příklad 1

Najděte derivaci funkce

Pod sinem nemáme jen písmeno „X“, ale celý výraz, takže nalezení derivace hned z tabulky nebude fungovat. Všimli jsme si také, že zde nelze použít první čtyři pravidla, zdá se, že existuje rozdíl, ale faktem je, že sinus nelze „roztrhat na kusy“:

V tomto příkladu je již z mých vysvětlení intuitivně jasné, že funkce je komplexní funkce a polynom je vnitřní funkce (vložení) a vnější funkce.

První krok co musíte udělat, když najdete derivaci komplexní funkce, je to pochopit, která funkce je vnitřní a která vnější.

V případě jednoduchých příkladů se zdá jasné, že pod sinus je vnořen polynom. Ale co když není vše zřejmé? Jak přesně určit, která funkce je vnější a která vnitřní? K tomu navrhuji použít následující techniku, kterou lze provést mentálně nebo v konceptu.

Představme si, že potřebujeme vypočítat hodnotu výrazu at na kalkulačce (místo jedné může být libovolné číslo).

Co budeme počítat jako první? Nejdříve budete muset provést následující akci: , proto bude polynom vnitřní funkcí:

Za druhé bude nutné najít, takže sinus – bude externí funkce:

Po nás VYPRODÁNO s vnitřními a vnějšími funkcemi je čas uplatnit pravidlo diferenciace komplexních funkcí .

Začněme se rozhodovat. Z lekce Jak najít derivát? pamatujeme si, že návrh řešení jakékoli derivace vždy začíná takto - výraz uzavřeme do hranatých závorek a dáme tah vpravo nahoře:

Nejprve najdeme derivaci externí funkce (sinus), podíváme se na tabulku derivací elementárních funkcí a všimneme si, že . Všechny tabulkové vzorce jsou také použitelné, pokud je „x“ nahrazeno složitým výrazem, v tomto případě:

Vezměte prosím na vědomí, že vnitřní funkce se nezměnilo, nedotýkáme se ho.

No, to je celkem zřejmé

Výsledek použití vzorce ve finální podobě to vypadá takto:

Konstantní faktor je obvykle umístěn na začátku výrazu:

Pokud dojde k nějakému nedorozumění, napište si řešení na papír a znovu si přečtěte vysvětlení.

Příklad 2

Najděte derivaci funkce

Příklad 3

Najděte derivaci funkce

Jako vždy zapisujeme:

Pojďme zjistit, kde máme vnější funkci a kde vnitřní. K tomu se snažíme (mentálně nebo v konceptu) vypočítat hodnotu výrazu v . Co byste měli udělat jako první? Nejprve musíte vypočítat, čemu se rovná základna: proto je polynom vnitřní funkcí:

A teprve potom se provádí umocňování, proto je mocninná funkce externí funkcí:

Podle vzorce Nejprve musíte najít derivaci externí funkce, v tomto případě stupeň. Požadovaný vzorec hledáme v tabulce: . Znovu opakujeme: jakýkoli tabulkový vzorec platí nejen pro „X“, ale také pro komplexní výraz. Tedy výsledek aplikace pravidla pro derivování komplexní funkce další:

Znovu zdůrazňuji, že když vezmeme derivaci vnější funkce, naše vnitřní funkce se nezmění:

Nyní zbývá jen najít velmi jednoduchou derivaci vnitřní funkce a výsledek trochu upravit:

Příklad 4

Najděte derivaci funkce

Toto je příklad, který můžete vyřešit sami (odpověď na konci lekce).

Pro upevnění vašeho chápání derivace komplexní funkce uvedu příklad bez komentáře, zkuste si na to přijít sami, důvod, kde je vnější a kde vnitřní funkce, proč jsou úlohy řešeny tímto způsobem?

Příklad 5

a) Najděte derivaci funkce

b) Najděte derivaci funkce

Příklad 6

Najděte derivaci funkce

Zde máme kořen, a abychom mohli kořen rozlišit, musí být reprezentován jako mocnina. Nejprve tedy funkci převedeme do tvaru vhodného pro derivování:

Při analýze funkce dojdeme k závěru, že součet tří členů je vnitřní funkcí a umocnění je vnější funkcí. Aplikujeme pravidlo derivace komplexních funkcí :

Opět znázorňujeme stupeň jako radikál (odmocninu) a pro derivaci vnitřní funkce použijeme jednoduché pravidlo pro derivování součtu:

Připraveno. Výraz můžete také zredukovat na společného jmenovatele v závorkách a zapsat vše jako jeden zlomek. Je to samozřejmě krásné, ale když vám vzniknou těžkopádné dlouhé derivace, je lepší to nedělat (snadno se splete, uděláte zbytečnou chybu a pro učitele bude nepohodlné to kontrolovat).

Příklad 7

Najděte derivaci funkce

Toto je příklad, který můžete vyřešit sami (odpověď na konci lekce).

Je zajímavé, že někdy místo pravidla pro derivování komplexní funkce můžete použít pravidlo pro derivování kvocientu , ale takové řešení bude vypadat jako neobvyklá perverze. Zde je typický příklad:

Příklad 8

Najděte derivaci funkce

Zde můžete použít pravidlo diferenciace kvocientu , ale mnohem výhodnější je najít derivaci pomocí pravidla derivace komplexní funkce:

Připravíme funkci pro derivování - posuneme mínus ze znaménka derivace a zvedneme kosinus do čitatele:

Kosinus je vnitřní funkce, umocňování je vnější funkce.
Použijme naše pravidlo :

Najdeme derivaci vnitřní funkce a resetujeme kosinus zpět:

Připraveno. V uvažovaném příkladu je důležité nenechat se zmást ve znameních. Mimochodem, zkuste to vyřešit pomocí pravidla , odpovědi se musí shodovat.

Příklad 9

Najděte derivaci funkce

Toto je příklad, který můžete vyřešit sami (odpověď na konci lekce).

Dosud jsme se zabývali případy, kdy jsme měli pouze jedno vnoření v komplexní funkci. V praktických úlohách se často můžete setkat s odvozeninami, kde se jako hnízdící panenky jedna do druhé vnořuje 3 nebo dokonce 4-5 funkcí najednou.

Příklad 10

Najděte derivaci funkce

Pojďme pochopit přílohy této funkce. Zkusme spočítat výraz pomocí experimentální hodnoty. Jak bychom počítali s kalkulačkou?

Nejprve musíte najít , což znamená, že arcsinus je nejhlubší vložení:

Tento arkussinus jedné by pak měl být na druhou:

A nakonec zvýšíme sedm na mocninu:

To znamená, že v tomto příkladu máme tři různé funkce a dvě vložení, přičemž nejvnitřnější funkcí je arkussinus a nejvzdálenější funkcí je exponenciální funkce.

Začněme se rozhodovat

Podle pravidla Nejprve musíte vzít derivaci vnější funkce. Podíváme se na tabulku derivací a najdeme derivaci exponenciální funkce: Jediný rozdíl je v tom, že místo „x“ máme komplexní výraz, který nepopírá platnost tohoto vzorce. Tedy výsledek aplikace pravidla pro derivování komplexní funkce další.

Velmi snadno zapamatovatelné.

No, nechoďme daleko, pojďme okamžitě uvažovat o inverzní funkci. Která funkce je inverzní k exponenciální funkci? Logaritmus:

V našem případě je základem číslo:

Takový logaritmus (tedy logaritmus se základem) se nazývá „přirozený“ a používáme pro něj speciální zápis: místo toho píšeme.

čemu se to rovná? Samozřejmě, .

Derivace přirozeného logaritmu je také velmi jednoduchá:

Příklady:

1. Najděte derivaci funkce.
2. Jaká je derivace funkce?

Odpovědi: Exponenciální a přirozený logaritmus jsou z derivační perspektivy jedinečně jednoduché funkce. Exponenciální a logaritmické funkce s jakoukoli jinou bází budou mít jinou derivaci, kterou budeme analyzovat později, až si projdeme pravidla derivování.

Pravidla diferenciace

Pravidla čeho? Zase nový termín, zase?!...

Diferenciace je proces hledání derivátu.

To je vše. Jak jinak lze tento proces nazvat jedním slovem? Ne derivace... Matematici nazývají diferenciál stejným přírůstkem funkce at. Tento výraz pochází z latinského differentia – rozdíl. Tady.

Při odvozování všech těchto pravidel použijeme dvě funkce, například a. Budeme také potřebovat vzorce pro jejich přírůstky:

Existuje celkem 5 pravidel.

Konstanta je vyjmuta z derivačního znaménka.

Pokud - nějaké konstantní číslo (konstanta), pak.

Toto pravidlo samozřejmě funguje i pro rozdíl: .

Pojďme to dokázat. Nech to být, nebo jednodušší.

Příklady.

Najděte derivace funkcí:

1. v bodě;
2. v bodě;
3. v bodě;
4. na místě.

Řešení:

1. (derivace je ve všech bodech stejná, protože jde o lineární funkci, pamatujete?);

Derivát produktu

Zde je vše podobné: zavedeme novou funkci a najdeme její přírůstek:

Derivát:

Příklady:

1. Najděte derivace funkcí a;
2. Najděte derivaci funkce v bodě.

Řešení:

Derivace exponenciální funkce

Nyní vaše znalosti stačí na to, abyste se naučili najít derivaci jakékoli exponenciální funkce, a nejen exponentů (zapomněli jste, co to je?).

Tak kde je nějaké číslo.

Derivaci funkce již známe, zkusme tedy naši funkci zredukovat na nový základ:

K tomu použijeme jednoduché pravidlo: . Pak:

No, povedlo se. Nyní zkuste najít derivaci a nezapomeňte, že tato funkce je složitá.

Stalo?

Zde se přesvědčte:

Ukázalo se, že vzorec je velmi podobný derivaci exponentu: jak byl, zůstává stejný, objevil se pouze faktor, což je jen číslo, ale ne proměnná.

Příklady:
Najděte derivace funkcí:

Odpovědi:

To je jen číslo, které se bez kalkulačky nedá spočítat, to znamená, že se nedá zapsat v jednodušší podobě. Proto jej v odpovědi ponecháme v této podobě.

Všimněte si, že zde je podíl dvou funkcí, takže použijeme odpovídající pravidlo diferenciace:

V tomto příkladu součin dvou funkcí:

Derivace logaritmické funkce

Tady je to podobné: derivaci přirozeného logaritmu už znáte:

Chcete-li tedy najít libovolný logaritmus s jiným základem, například:

Musíme tento logaritmus zmenšit na základnu. Jak změníte základ logaritmu? Doufám, že si pamatujete tento vzorec:

Teprve teď místo toho napíšeme:

Jmenovatel je jednoduše konstanta (konstantní číslo, bez proměnné). Derivát se získá velmi jednoduše:

Derivace exponenciálních a logaritmických funkcí se v jednotné státní zkoušce téměř nikdy nenacházejí, ale nebude zbytečné je znát.

Derivace komplexní funkce.

Co je to "komplexní funkce"? Ne, toto není logaritmus ani arkustangens. Těmto funkcím může být obtížné porozumět (ačkoli pokud se vám zdá logaritmus obtížný, přečtěte si téma „Logaritmy“ a budete v pořádku), ale z matematického hlediska slovo „složitý“ neznamená „obtížný“.

Představte si malý dopravníkový pás: dva lidé sedí a provádějí nějaké akce s nějakými předměty. První například zabalí čokoládovou tyčinku do obalu a druhý ji převáže stuhou. Výsledkem je složený objekt: čokoládová tyčinka zabalená a převázaná stuhou. Chcete-li sníst čokoládovou tyčinku, musíte provést opačné kroky v opačném pořadí.

Vytvořme podobnou matematickou pipeline: nejprve najdeme kosinus čísla a poté odmocnime výsledné číslo. Takže dostaneme číslo (čokoláda), já najdu jeho kosinus (obal) a pak urovnáte, co jsem dostal (svažte to stuhou). Co se stalo? Funkce. Toto je příklad komplexní funkce: když, abychom zjistili její hodnotu, provedeme první akci přímo s proměnnou a poté druhou akci s tím, co vyplynulo z první.

Jinými slovy, komplexní funkce je funkce, jejímž argumentem je jiná funkce: .

Pro náš příklad, .

Stejné kroky můžeme snadno provést v opačném pořadí: nejprve to odmocníte a já pak hledám kosinus výsledného čísla: . Je snadné odhadnout, že výsledek bude téměř vždy jiný. Důležitá vlastnost komplexních funkcí: když se změní pořadí akcí, změní se funkce.

Druhý příklad: (totéž). .

Akce, kterou uděláme jako poslední, bude vyvolána „externí“ funkce, a akce provedená jako první – podle toho „vnitřní“ funkce(jedná se o neformální názvy, používám je pouze k vysvětlení látky jednoduchým jazykem).

Zkuste sami určit, která funkce je vnější a která vnitřní:

Odpovědi: Oddělení vnitřních a vnějších funkcí je velmi podobné změně proměnných: například ve funkci

1. Jakou akci provedeme jako první? Nejprve vypočítejme sinus a teprve potom jej počítejme. To znamená, že jde o vnitřní funkci, ale o vnější.
   A původní funkcí je jejich složení: .
2. Interní: ; externí: .
   Vyšetření: .
3. Interní: ; externí: .
   Vyšetření: .
4. Interní: ; externí: .
   Vyšetření: .
5. Interní: ; externí: .
   Vyšetření: .

Změníme proměnné a dostaneme funkci.

Nyní vytáhneme naši čokoládovou tyčinku a budeme hledat derivát. Postup je vždy obrácený: nejprve hledáme derivaci vnější funkce, poté výsledek vynásobíme derivací vnitřní funkce. Ve vztahu k původnímu příkladu to vypadá takto:

Další příklad:

Pojďme tedy konečně formulovat oficiální pravidlo:

Algoritmus pro nalezení derivace komplexní funkce:

Vypadá to jednoduše, že?

Podívejme se na příklady:

Řešení:

1) Interní: ;

Externí: ;

2) Interní: ;

(Jen to teď nezkoušejte odříznout! Z pod kosinusu nic nevychází, pamatujete?)

3) Interní: ;

Externí: ;

Okamžitě je jasné, že se jedná o tříúrovňovou komplexní funkci: vždyť to už je komplexní funkce sama o sobě a navíc z ní extrahujeme kořen, to znamená, že provedeme třetí akci (dáme čokoládu do obalu a se stuhou v kufříku). Není ale důvod se bát: i tak tuto funkci „rozbalíme“ ve stejném pořadí jako obvykle: od konce.

To znamená, že nejprve rozlišujeme kořen, potom kosinus a teprve potom výraz v závorkách. A pak to všechno znásobíme.

V takových případech je vhodné akce očíslovat. To znamená, že si představme, co víme. V jakém pořadí provedeme akce pro výpočet hodnoty tohoto výrazu? Podívejme se na příklad:

Čím později je akce provedena, tím „externější“ bude odpovídající funkce. Pořadí akcí je stejné jako dříve:

Zde je hnízdění obecně 4úrovňové. Pojďme určit postup.

1. Radikální vyjádření. .

2. Kořen. .

3. Sinus. .

4. Čtverec. .

5. Dejte to všechno dohromady:

DERIVÁT. KRÁTCE O HLAVNÍCH VĚCÍCH

Derivace funkce- poměr přírůstku funkce k přírůstku argumentu pro nekonečně malý přírůstek argumentu:

Základní deriváty:

Pravidla rozlišování:

Konstanta je vyjmuta z derivačního znaménka:

Derivát součtu:

Derivát produktu:

Derivát kvocientu:

Derivace komplexní funkce:

Algoritmus pro nalezení derivace komplexní funkce:

1. Definujeme „vnitřní“ funkci a najdeme její derivaci.
2. Definujeme „externí“ funkci a najdeme její derivaci.
3. Výsledky prvního a druhého bodu vynásobíme.