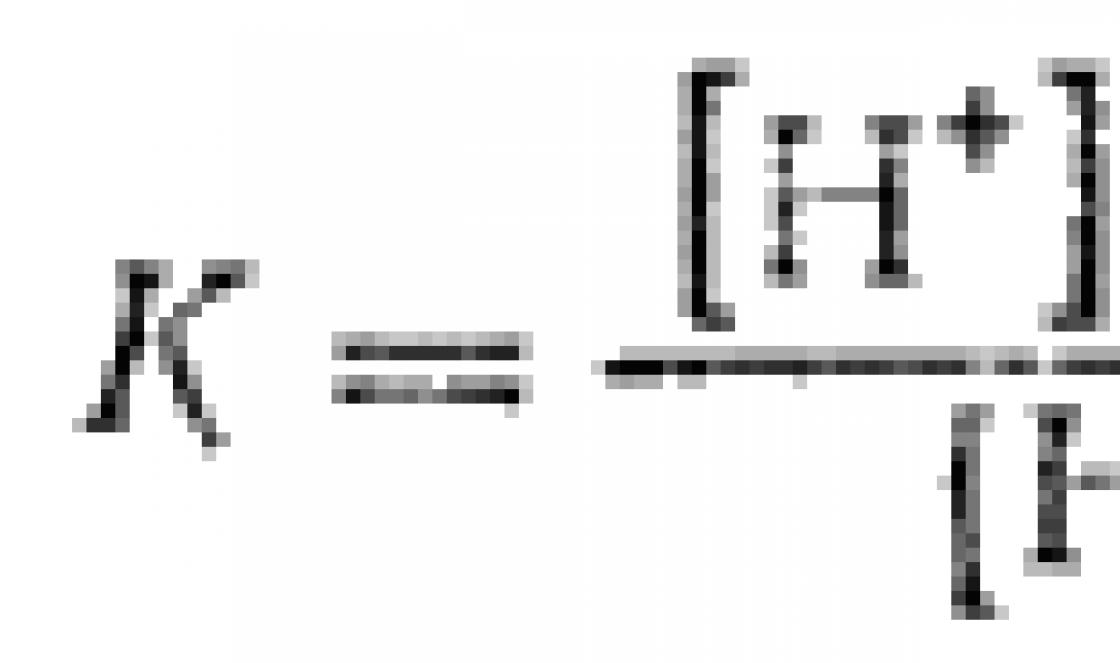The distribution function of a random variable X is the function F(x), which expresses for each x the probability that the random variable X will take the value, smaller x

Example 2.5. Given a distribution series of a random variable

Find and graphically depict its distribution function. Solution. According to the definition

F(jc) = 0 at X X

F(x) = 0.4 + 0.1 = 0.5 at 4 F(x) = 0.5 + 0.5 = 1 at X > 5.

So (see Fig. 2.1):

Properties of the distribution function:

1. The distribution function of a random variable is a non-negative function between zero and one:

2. The distribution function of a random variable is a non-decreasing function on the entire numerical axis, i.e. at X 2 >x

3. At minus infinity, the distribution function is equal to zero, at plus infinity it is equal to one, i.e.

4. Probability of hitting a random variable X in the interval is equal to a certain integral of its probability density ranging from A before b(see Fig. 2.2), i.e.

Rice. 2.2

3. The distribution function of a continuous random variable (see Fig. 2.3) can be expressed through the probability density according to the formula:

F(x)= Jp(*)*. (2.10)

4. The improper integral in infinite limits of the probability density of a continuous random variable is equal to unity:

Geometrically properties / and 4 probability densities mean that its graph is distribution curve - lies not below the x-axis, and the total area of ​​the figure, bounded by the distribution curve and the x-axis, equal to one.

For a continuous random variable X expected value M(X) and variance D(X) are determined by the formulas:

(if the integral is absolutely convergent); or

(if the above integrals converge).

Along with the numerical characteristics noted above, the concept of quantiles and percentage points is used to describe a random variable.

Quantile level q(or q-quantile) is such a valuex qrandom variable, at which its distribution function takes the value, equal to q, i.e.

• 100The q%-ou point is the quantile X~ q.
• ? Example 2.8.

Based on the data in Example 2.6, find the quantile xqj and the 30% random variable point X.

Solution. By definition (2.16) F(xo t3)= 0.3, i.e.

~Y~ = 0.3, where does the quantile come from? x 0 3 = 0.6. 30% random variable point X, or quantile X)_o,z = xoj"is found similarly from the equation ^ = 0.7. where *,= 1.4. ?

Among the numerical characteristics of a random variable there are initial v* and central R* moments of kth order, determined for discrete and continuous random variables by the formulas:

We can highlight the most common laws of distribution of discrete random variables:

• Binomial distribution law
• Poisson distribution law
• Geometric distribution law
• Hypergeometric distribution law

For given distributions of discrete random variables, the calculation of the probabilities of their values, as well as numerical characteristics (mathematical expectation, variance, etc.) is carried out using certain “formulas”. Therefore, it is very important to know these types of distributions and their basic properties.

1. Binomial distribution law.

A discrete random variable $X$ is subject to the binomial probability distribution law if it takes values ​​$0,\ 1,\ 2,\ \dots ,\ n$ with probabilities $P\left(X=k\right)=C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k)$. In fact, the random variable $X$ is the number of occurrences of event $A$ in $n$ independent trials. Law of probability distribution of random variable $X$:

$\begin(array)(|c|c|)
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end(array)$

For such a random variable, the mathematical expectation is $M\left(X\right)=np$, the variance is $D\left(X\right)=np\left(1-p\right)$.

Example . The family has two children. Assuming the probabilities of having a boy and a girl equal to $0.5$, find the law of distribution of the random variable $\xi$ - the number of boys in the family.

Let the random variable $\xi $ be the number of boys in the family. Values ​​that $\xi can take:\ 0,\ ​​1,\ 2$. The probabilities of these values ​​can be found using the formula $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k)$, where $n =2$ is the number of independent trials, $p=0.5$ is the probability of an event occurring in a series of $n$ trials. We get:

$P\left(\xi =0\right)=C^0_2\cdot (0,5)^0\cdot (\left(1-0,5\right))^(2-0)=(0, 5)^2=0.25;$

$P\left(\xi =1\right)=C^1_2\cdot 0.5\cdot (\left(1-0.5\right))^(2-1)=2\cdot 0.5\ cdot 0.5=0.5;$

$P\left(\xi =2\right)=C^2_2\cdot (0.5)^2\cdot (\left(1-0.5\right))^(2-2)=(0, 5)^2=0.25.$

Then the distribution law of the random variable $\xi $ is the correspondence between the values ​​$0,\ 1,\ 2$ and their probabilities, that is:

$\begin(array)(|c|c|)
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0.25 & 0.5 & 0.25 \\
\hline
\end(array)$

The sum of the probabilities in the distribution law should be equal to $1$, that is, $\sum _(i=1)^(n)P(\xi _((\rm i)))=0.25+0.5+0, 25=$1.

Expectation $M\left(\xi \right)=np=2\cdot 0.5=1$, variance $D\left(\xi \right)=np\left(1-p\right)=2\ cdot 0.5\cdot 0.5=0.5$, standard deviation $\sigma \left(\xi \right)=\sqrt(D\left(\xi \right))=\sqrt(0.5 )\approx $0.707.

2. Poisson distribution law.

If a discrete random variable $X$ can only take non-negative integer values ​​$0,\ 1,\ 2,\ \dots ,\ n$ with probabilities $P\left(X=k\right)=(((\lambda )^k )\over (k}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.!}

Comment. The peculiarity of this distribution is that, based on experimental data, we find estimates $M\left(X\right),\ D\left(X\right)$, if the obtained estimates are close to each other, then we have reason to assert that the random variable is subject to the Poisson distribution law.

Example . Examples of random variables subject to the Poisson distribution law can be: the number of cars that will be served by a gas station tomorrow; number of defective items in manufactured products.

Example . The factory sent $500$ of products to the base. The probability of damage to the product in transit is $0.002$. Find the law of distribution of the random variable $X$ equal to the number of damaged products; what is $M\left(X\right),\ D\left(X\right)$.

Let the discrete random variable $X$ be the number of damaged products. Such a random variable is subject to the Poisson distribution law with the parameter $\lambda =np=500\cdot 0.002=1$. The probabilities of the values ​​are equal to $P\left(X=k\right)=(((\lambda )^k)\over (k}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.!}

$P\left(X=0\right)=((1^0)\over (0}\cdot e^{-1}=0,368;$!}

$P\left(X=1\right)=((1^1)\over (1}\cdot e^{-1}=0,368;$!}

$P\left(X=2\right)=((1^2)\over (2}\cdot e^{-1}=0,184;$!}

$P\left(X=3\right)=((1^3)\over (3}\cdot e^{-1}=0,061;$!}

$P\left(X=4\right)=((1^4)\over (4}\cdot e^{-1}=0,015;$!}

$P\left(X=5\right)=((1^5)\over (5}\cdot e^{-1}=0,003;$!}

$P\left(X=6\right)=((1^6)\over (6}\cdot e^{-1}=0,001;$!}

$P\left(X=k\right)=(((\lambda )^k)\over (k}\cdot e^{-\lambda }$!}

Distribution law of random variable $X$:

$\begin(array)(|c|c|)
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0.368; & 0.368 & 0.184 & 0.061 & 0.015 & 0.003 & 0.001 & ... & (((\lambda )^k)\over (k}\cdot e^{-\lambda } \\!}
\hline
\end(array)$

For such a random variable, the mathematical expectation and variance are equal to each other and equal to the parameter $\lambda $, that is, $M\left(X\right)=D\left(X\right)=\lambda =1$.

3. Geometric distribution law.

If a discrete random variable $X$ can only take natural values ​​$1,\ 2,\ \dots ,\ n$ with probabilities $P\left(X=k\right)=p(\left(1-p\right)) ^(k-1),\ k=1,\ 2,\ 3,\ \dots $, then they say that such a random variable $X$ is subject to the geometric law of probability distribution. In fact, the geometric distribution is a Bernoulli test until the first success.

Example . Examples of random variables that have a geometric distribution can be: the number of shots before the first hit on the target; number of device tests until the first failure; the number of coin tosses until the first head comes up, etc.

The mathematical expectation and variance of a random variable subject to geometric distribution are respectively equal to $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^ $2.

Example . On the way of fish movement to the spawning site there is a $4$ lock. The probability of fish passing through each lock is $p=3/5$. Construct a series of distribution of the random variable $X$ - the number of locks passed by the fish before the first detention at the lock. Find $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.

Let the random variable $X$ be the number of locks passed by the fish before the first arrest at the lock. Such a random variable is subject to the geometric law of probability distribution. Values ​​that the random variable $X can take:$ 1, 2, 3, 4. The probabilities of these values ​​are calculated using the formula: $P\left(X=k\right)=pq^(k-1)$, where: $ p=2/5$ - probability of fish being detained through the lock, $q=1-p=3/5$ - probability of fish passing through the lock, $k=1,\ 2,\ 3,\ 4$.

$P\left(X=1\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^0=((2)\ over (5))=0.4;$

$P\left(X=2\right)=((2)\over (5))\cdot ((3)\over (5))=((6)\over (25))=0.24; $

$P\left(X=3\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^2=((2)\ over (5))\cdot ((9)\over (25))=((18)\over (125))=0.144;$

$P\left(X=4\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^3+(\left(( (3)\over (5))\right))^4=((27)\over (125))=0.216.$

$\begin(array)(|c|c|)
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0.4 & 0.24 & 0.144 & 0.216 \\
\hline
\end(array)$

Expected value:

$M\left(X\right)=\sum^n_(i=1)(x_ip_i)=1\cdot 0.4+2\cdot 0.24+3\cdot 0.144+4\cdot 0.216=2.176.$

Dispersion:

$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2=)0.4\cdot (\ left(1-2,176\right))^2+0.24\cdot (\left(2-2,176\right))^2+0.144\cdot (\left(3-2,176\right))^2+$

$+\0.216\cdot (\left(4-2,176\right))^2\approx 1.377.$

Standard deviation:

$\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(1,377)\approx 1,173.$

4. Hypergeometric distribution law.

If $N$ objects, among which $m$ objects have a given property. $n$ objects are randomly retrieved without returning, among which there were $k$ objects that have a given property. The hypergeometric distribution makes it possible to estimate the probability that exactly $k$ objects in the sample have a given property. Let the random variable $X$ be the number of objects in the sample that have a given property. Then the probabilities of the values ​​of the random variable $X$:

$P\left(X=k\right)=((C^k_mC^(n-k)_(N-m))\over (C^n_N))$

Comment. The statistical function HYPERGEOMET of the Excel $f_x$ function wizard allows you to determine the probability that a certain number of tests will be successful.

$f_x\to$ statistical$\to$ HYPERGEOMET$\to$ OK. A dialog box will appear that you need to fill out. In the column Number_of_successes_in_sample indicate the value $k$. sample_size equals $n$. In the column Number_of_successes_in_together indicate the value $m$. population_size equals $N$.

The mathematical expectation and variance of a discrete random variable $X$, subject to the geometric distribution law, are respectively equal to $M\left(X\right)=nm/N$, $D\left(X\right)=((nm\left(1 -((m)\over (N))\right)\left(1-((n)\over (N))\right))\over (N-1))$.

Example . The bank's credit department employs 5 specialists with higher financial education and 3 specialists with higher legal education. The bank's management decided to send 3 specialists to improve their qualifications, selecting them in random order.

a) Make a distribution series for the number of specialists with higher financial education who can be sent to improve their skills;

b) Find the numerical characteristics of this distribution.

Let the random variable $X$ be the number of specialists with higher financial education among the three selected ones. Values ​​that $X can take: 0,\ 1,\ 2,\ 3$. This random variable $X$ is distributed according to a hypergeometric distribution with the following parameters: $N=8$ - population size, $m=5$ - number of successes in the population, $n=3$ - sample size, $k=0,\ 1, \2,\3$ - number of successes in the sample. Then the probabilities $P\left(X=k\right)$ can be calculated using the formula: $P(X=k)=(C_(m)^(k) \cdot C_(N-m)^(n-k) \over C_( N)^(n) ) $. We have:

$P\left(X=0\right)=((C^0_5\cdot C^3_3)\over (C^3_8))=((1)\over (56))\approx 0.018;$

$P\left(X=1\right)=((C^1_5\cdot C^2_3)\over (C^3_8))=((15)\over (56))\approx 0.268;$

$P\left(X=2\right)=((C^2_5\cdot C^1_3)\over (C^3_8))=((15)\over (28))\approx 0.536;$

$P\left(X=3\right)=((C^3_5\cdot C^0_3)\over (C^3_8))=((5)\over (28))\approx 0.179.$

Then the distribution series of the random variable $X$:

$\begin(array)(|c|c|)
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0.018 & 0.268 & 0.536 & 0.179 \\
\hline
\end(array)$

Let us calculate the numerical characteristics of the random variable $X$ using the general formulas of the hypergeometric distribution.

$M\left(X\right)=((nm)\over (N))=((3\cdot 5)\over (8))=((15)\over (8))=1,875.$

$D\left(X\right)=((nm\left(1-((m)\over (N))\right)\left(1-((n)\over (N))\right)) \over (N-1))=((3\cdot 5\cdot \left(1-((5)\over (8))\right)\cdot \left(1-((3)\over (8 ))\right))\over (8-1))=((225)\over (448))\approx 0.502.$

$\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(0.502)\approx 0.7085.$

Random variable A variable is called a variable that, as a result of each test, takes on one previously unknown value, depending on random reasons. Random variables are denoted by capital Latin letters: $X,\ Y,\ Z,\ \dots $ According to their type, random variables can be discrete And continuous.

Discrete random variable- this is a random variable whose values ​​can be no more than countable, that is, either finite or countable. By countability we mean that the values ​​of a random variable can be numbered.

Example 1 . Here are examples of discrete random variables:

a) the number of hits on the target with $n$ shots, here the possible values ​​are $0,\ 1,\ \dots ,\ n$.

b) the number of emblems dropped when tossing a coin, here the possible values ​​are $0,\ 1,\ \dots ,\ n$.

c) the number of ships arriving on board (a countable set of values).

d) the number of calls arriving at the PBX (countable set of values).

1. Law of probability distribution of a discrete random variable.

A discrete random variable $X$ can take values ​​$x_1,\dots ,\ x_n$ with probabilities $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. The correspondence between these values ​​and their probabilities is called law of distribution of a discrete random variable. As a rule, this correspondence is specified using a table, the first line of which indicates the values ​​$x_1,\dots ,\ x_n$, and the second line contains the probabilities $p_1,\dots ,\ p_n$ corresponding to these values.

$\begin(array)(|c|c|)
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end(array)$

Example 2 . Let the random variable $X$ be the number of points rolled when tossing a die. Such a random variable $X$ can take the following values: $1,\ 2,\ 3,\ 4,\ 5,\ 6$. The probabilities of all these values ​​are equal to $1/6$. Then the law of probability distribution of the random variable $X$:

$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline

\hline
\end(array)$

Comment. Since in the distribution law of a discrete random variable $X$ the events $1,\ 2,\ \dots ,\ 6$ form a complete group of events, then the sum of the probabilities must be equal to one, that is, $\sum(p_i)=1$.

2. Mathematical expectation of a discrete random variable.

Expectation of a random variable sets its “central” meaning. For a discrete random variable, the mathematical expectation is calculated as the sum of the products of the values ​​$x_1,\dots ,\ x_n$ and the probabilities $p_1,\dots ,\ p_n$ corresponding to these values, that is: $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$. In English-language literature, another notation $E\left(X\right)$ is used.

Properties of mathematical expectation$M\left(X\right)$:

1. $M\left(X\right)$ lies between the smallest and largest values ​​of the random variable $X$.
2. The mathematical expectation of a constant is equal to the constant itself, i.e. $M\left(C\right)=C$.
3. The constant factor can be taken out of the sign of the mathematical expectation: $M\left(CX\right)=CM\left(X\right)$.
4. The mathematical expectation of the sum of random variables is equal to the sum of their mathematical expectations: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
5. The mathematical expectation of the product of independent random variables is equal to the product of their mathematical expectations: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.

Example 3 . Let's find the mathematical expectation of the random variable $X$ from example $2$.

$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\over (6))+4\cdot ((1)\over (6))+5\cdot ((1)\over (6))+6\cdot ((1 )\over (6))=3.5.$$

We can notice that $M\left(X\right)$ lies between the smallest ($1$) and largest ($6$) values ​​of the random variable $X$.

Example 4 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=2$. Find the mathematical expectation of the random variable $3X+5$.

Using the above properties, we get $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2 +5=$11.

Example 5 . It is known that the mathematical expectation of the random variable $X$ is equal to $M\left(X\right)=4$. Find the mathematical expectation of the random variable $2X-9$.

Using the above properties, we get $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4 -9=-1$.

3. Dispersion of a discrete random variable.

Possible values ​​of random variables with equal mathematical expectations can disperse differently around their average values. For example, in two student groups the average score for the exam in probability theory turned out to be 4, but in one group everyone turned out to be good students, and in the other group there were only C students and excellent students. Therefore, there is a need for a numerical characteristic of a random variable that would show the spread of the values ​​of the random variable around its mathematical expectation. This characteristic is dispersion.

Variance of a discrete random variable$X$ is equal to:

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$

In English literature the notation $V\left(X\right),\ Var\left(X\right)$ is used. Very often the variance $D\left(X\right)$ is calculated using the formula $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\left(X \right)\right))^2$.

Dispersion properties$D\left(X\right)$:

1. The variance is always greater than or equal to zero, i.e. $D\left(X\right)\ge 0$.
2. The variance of the constant is zero, i.e. $D\left(C\right)=0$.
3. The constant factor can be taken out of the sign of the dispersion provided that it is squared, i.e. $D\left(CX\right)=C^2D\left(X\right)$.
4. The variance of the sum of independent random variables is equal to the sum of their variances, i.e. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
5. The variance of the difference between independent random variables is equal to the sum of their variances, i.e. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.

Example 6 . Let's calculate the variance of the random variable $X$ from example $2$.

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3.5\right))^2+((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +((1)\over (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\approx 2.92.$$

Example 7 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=2$. Find the variance of the random variable $4X+1$.

Using the above properties, we find $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\ left(X\right)=16\cdot 2=32$.

Example 8 . It is known that the variance of the random variable $X$ is equal to $D\left(X\right)=3$. Find the variance of the random variable $3-2X$.

Using the above properties, we find $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\ left(X\right)=4\cdot 3=12$.

4. Distribution function of a discrete random variable.

The method of representing a discrete random variable in the form of a distribution series is not the only one, and most importantly, it is not universal, since a continuous random variable cannot be specified using a distribution series. There is another way to represent a random variable - the distribution function.

Distribution function random variable $X$ is called a function $F\left(x\right)$, which determines the probability that the random variable $X$ will take a value less than some fixed value $x$, that is, $F\left(x\right )=P\left(X< x\right)$

Properties of the distribution function:

1. $0\le F\left(x\right)\le 1$.
2. The probability that the random variable $X$ will take values ​​from the interval $\left(\alpha ;\ \beta \right)$ is equal to the difference between the values ​​of the distribution function at the ends of this interval: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
3. $F\left(x\right)$ - non-decreasing.
4. $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$.

Example 9 . Let us find the distribution function $F\left(x\right)$ for the distribution law of the discrete random variable $X$ from example $2$.

$\begin(array)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(array)$

If $x\le 1$, then, obviously, $F\left(x\right)=0$ (including for $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).

If $1< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

If $2< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

If $3< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

If $4< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

If $5< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

If $x > 6$, then $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$.

So $F(x)=\left\(\begin(matrix)
0,\ at\ x\le 1,\\
1/6,at\ 1< x\le 2,\\
1/3,\ at\ 2< x\le 3,\\
1/2,at\ 3< x\le 4,\\
2/3,\ at\ 4< x\le 5,\\
5/6,\ at\ 4< x\le 5,\\
1,\ for\ x > 6.
\end(matrix)\right.$

LAW OF DISTRIBUTION AND CHARACTERISTICS

RANDOM VARIABLES

Random variables, their classification and methods of description.

A random quantity is a quantity that, as a result of experiment, can take on one or another value, but which one is not known in advance. For a random variable, therefore, you can only specify values, one of which it will definitely take as a result of experiment. In what follows we will call these values ​​possible values ​​of the random variable. Since a random variable quantitatively characterizes the random result of an experiment, it can be considered as a quantitative characteristic of a random event.

Random variables are usually denoted by capital letters of the Latin alphabet, for example, X..Y..Z, and their possible values ​​by corresponding small letters.

There are three types of random variables:

Discrete; Continuous; Mixed.

Discrete is a random variable whose number of possible values ​​forms a countable set. In turn, a set whose elements can be numbered is called countable. The word "discrete" comes from the Latin discretus, meaning "discontinuous, consisting of separate parts".

Example 1. A discrete random variable is the number of defective parts X in a batch of nproducts. Indeed, the possible values ​​of this random variable are a series of integers from 0 to n.

Example 2. A discrete random variable is the number of shots before the first hit on the target. Here, as in Example 1, the possible values ​​can be numbered, although in the limiting case the possible value is an infinitely large number.

Continuous is a random variable whose possible values ​​continuously fill a certain interval of the numerical axis, sometimes called the interval of existence of this random variable. Thus, on any finite interval of existence, the number of possible values ​​of a continuous random variable is infinitely large.

Example 3. A continuous random variable is the monthly electricity consumption of an enterprise.

Example 4. A continuous random variable is the error in measuring height using an altimeter. Let it be known from the operating principle of the altimeter that the error lies in the range from 0 to 2 m. Therefore, the interval of existence of this random variable is the interval from 0 to 2 m.

Law of distribution of random variables.

A random variable is considered completely specified if its possible values ​​are indicated on the numerical axis and the distribution law is established.

Law of distribution of a random variable is a relation that establishes a connection between the possible values ​​of a random variable and the corresponding probabilities.

A random variable is said to be distributed according to a given law, or subject to a given distribution law. A number of probabilities, distribution function, probability density, and characteristic function are used as distribution laws.

The distribution law gives a complete probable description of a random variable. According to the distribution law, one can judge before experiment which possible values ​​of a random variable will appear more often and which less often.

For a discrete random variable, the distribution law can be specified in the form of a table, analytically (in the form of a formula) and graphically.

The simplest form of specifying the distribution law of a discrete random variable is a table (matrix), which lists in ascending order all possible values ​​of the random variable and their corresponding probabilities, i.e.

Such a table is called a distribution series of a discrete random variable. 1

Events X 1, X 2,..., X n, consisting in the fact that as a result of the test, the random variable X will take the values ​​x 1, x 2,... x n, respectively, are inconsistent and the only possible ones (since the table lists all possible values ​​of a random variable), i.e. form a complete group. Therefore, the sum of their probabilities is equal to 1. Thus, for any discrete random variable

(This unit is somehow distributed among the values ​​of the random variable, hence the term "distribution").

The distribution series can be depicted graphically if the values ​​of the random variable are plotted along the abscissa axis, and their corresponding probabilities are plotted along the ordinate axis. The connection of the obtained points forms a broken line called a polygon or polygon of the probability distribution (Fig. 1).

Example The lottery includes: a car worth 5,000 den. units, 4 TVs costing 250 den. units, 5 video recorders worth 200 den. units A total of 1000 tickets are sold for 7 days. units Draw up a distribution law for the net winnings received by a lottery participant who bought one ticket.

Solution. Possible values ​​of the random variable X - the net winnings per ticket - are equal to 0-7 = -7 money. units (if the ticket did not win), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 den. units (if the ticket has the winnings of a VCR, TV or car, respectively). Considering that out of 1000 tickets the number of non-winners is 990, and the indicated winnings are 5, 4 and 1, respectively, and using the classical definition of probability, we obtain.