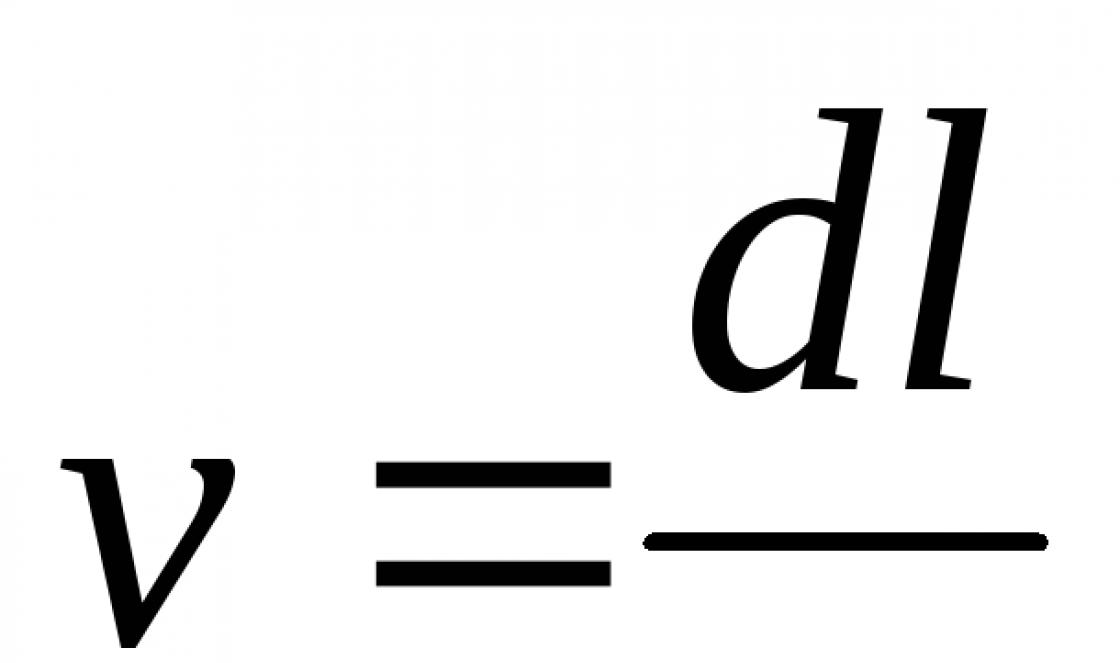"Lesson of the Pythagorean theorem" - The Pythagorean theorem. Determine the type of quadrilateral KMNP. Warm up. Introduction to the theorem. Determine the type of triangle: Lesson plan: Historical digression. Solving simple problems. And find a ladder 125 feet long. Calculate the height CF of trapezoid ABCD. Proof. Showing pictures. Proof of the theorem.
"Volume of a prism" - The concept of a prism. direct prism. The volume of the original prism is equal to the product S · h. How to find the volume of a straight prism? The prism can be divided into straight triangular prisms with height h. Draw the altitude of triangle ABC. The solution of the problem. Lesson goals. Basic steps in proving the direct prism theorem? Study of the prism volume theorem.
"Prism polyhedra" - Define a polyhedron. DABC is a tetrahedron, a convex polyhedron. The use of prisms. Where are prisms used? ABCDMP is an octahedron, made up of eight triangles. ABCDA1B1C1D1 is a parallelepiped, a convex polyhedron. Convex polyhedron. The concept of a polyhedron. Polyhedron A1A2..AnB1B2..Bn is a prism.
"Prism class 10" - A prism is a polyhedron whose faces are in parallel planes. The use of a prism in everyday life. Sside = Pbased. + h For a straight prism: Sp.p = Pmain. h + 2Smain. Inclined. Correct. Straight. Prism. Formulas for finding the area. The use of prism in architecture. Sp.p \u003d S side + 2 S based.
"Proof of the Pythagorean theorem" - Geometric proof. The meaning of the Pythagorean theorem. Pythagorean theorem. Euclid's proof. "In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs." Proofs of the theorem. The significance of the theorem is that most of the theorems of geometry can be deduced from it or with its help.
General information about a straight prism
The lateral surface of the prism (more precisely, the lateral surface area) is called sum side face areas. The total surface of the prism is equal to the sum of the lateral surface and the areas of the bases.
Theorem 19.1. Side surface a straight prism is equal to the product of the perimeter of the base and the height of the prism, i.e., the length of the side edge.
Proof. Side faces straight prisms are rectangles. The bases of these rectangles are the sides of the polygon lying at the base of the prism, and the heights are equal to the length of the side edges. It follows that the lateral surface of the prism is equal to
S = a 1 l + a 2 l + ... + a n l = pl,
where a 1 and n are the lengths of the ribs of the base, p is the perimeter of the base of the prism, and I is the length of the side ribs. The theorem has been proven.
Practical task
Task (22) . In an inclined prism section, perpendicular to the side edges and intersecting all side ribs. Find the side surface of the prism if the perimeter of the section is p and the side edges are l.
Solution. The plane of the section drawn divides the prism into two parts (Fig. 411). Let's subject one of them to a parallel translation that combines the bases of the prism. In this case, we obtain a straight prism, in which the section of the original prism serves as the base, and the side edges are equal to l. This prism has the same side surface as the original one. Thus, the side surface of the original prism is equal to pl.
Generalization of the topic
And now let's try with you to summarize the topic of the prism and remember what properties a prism has.

Prism Properties
First, for a prism, all its bases are equal polygons;
Secondly, for a prism, all its side faces are parallelograms;
Thirdly, in such a multifaceted figure as a prism, all side edges are equal;
Also, it should be remembered that polyhedra such as prisms can be straight and inclined.
What is a straight prism?
If the side edge of a prism is perpendicular to the plane of its base, then such a prism is called a straight line.
It will not be superfluous to recall that the side faces of a straight prism are rectangles.
What is an oblique prism?
But if the side edge of the prism is not located perpendicular to the plane of its base, then we can safely say that this is an inclined prism.
What is the right prism?

If at the base of a straight prism lies regular polygon, then such a prism is correct.
Now let's recall the properties that a regular prism has.
Properties of a regular prism
First, always grounds right prism are regular polygons;
Secondly, if we consider the side faces of a regular prism, then they are always equal rectangles;
Thirdly, if we compare the sizes of the side ribs, then in the correct prism they are always equal.
Fourth, a regular prism is always straight;
Fifthly, if in a regular prism the side faces are in the form of squares, then such a figure, as a rule, is called a semi-regular polygon.
Prism section
Now let's look at the cross section of a prism:

Homework
And now let's try to consolidate the studied topic by solving problems.
Let's draw an inclined triangular prism, in which the distance between its edges will be: 3 cm, 4 cm and 5 cm, and the side surface of this prism will be equal to 60 cm2. With these parameters, find the lateral edge of the given prism.
And you know that geometric figures constantly surround us not only in geometry lessons, but also in Everyday life there are objects that resemble one or another geometric figure.

Every home, school or work has a computer, the system unit of which is in the form of a straight prism.
If you pick up a simple pencil, you will see that the main part of the pencil is a prism.
Walking along the main street of the city, we see that under our feet lies a tile that has the shape of a hexagonal prism.
A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions
Definition 1. Prismatic surface
Theorem 1. On parallel sections of a prismatic surface
Definition 2. Perpendicular section of a prismatic surface
Definition 3. Prism
Definition 4. Prism height
Definition 5. Direct prism
Theorem 2. The area of the lateral surface of the prism
Parallelepiped :
Definition 6. Parallelepiped
Theorem 3. On the intersection of the diagonals of a parallelepiped
Definition 7. Right parallelepiped
Definition 8. Rectangular parallelepiped
Definition 9. Dimensions of a parallelepiped
Definition 10. Cube
Definition 11. Rhombohedron
Theorem 4. On diagonals cuboid
Theorem 5. Volume of a prism
Theorem 6. Volume of a straight prism
Theorem 7. Volume of a rectangular parallelepiped
prism a polyhedron is called, in which two faces (bases) lie in parallel planes, and the edges that do not lie in these faces are parallel to each other.
Faces other than bases are called lateral.
The sides of the side faces and bases are called prism edges, the ends of the edges are called the tops of the prism. Lateral ribs called edges that do not belong to the bases. The union of side faces is called side surface of the prism, and the union of all faces is called full surface of the prism. Prism height called the perpendicular dropped from the point of the upper base to the plane of the lower base or the length of this perpendicular.  straight prism called a prism, in which the side edges are perpendicular to the planes of the bases.
straight prism called a prism, in which the side edges are perpendicular to the planes of the bases.  Correct called a straight prism (Fig. 3), at the base of which lies a regular polygon.
Correct called a straight prism (Fig. 3), at the base of which lies a regular polygon.
Designations:
l - side rib;
P - base perimeter;
S o - base area;
H - height;
P ^ - perimeter of the perpendicular section;
S b - side surface area;
V - volume;
S p - area full surface prisms.
|
V=SH |
*It is assumed that every two consecutive planes intersect and that the last plane intersects the first.

Theorem 1 . Sections of a prismatic surface by planes parallel to each other (but not parallel to its edges) are equal polygons.
Let ABCDE and A"B"C"D"E" be sections of a prismatic surface by two parallel planes. To verify that these two polygons are equal, it is enough to show that triangles ABC and A"B"C" are equal and have the same direction of rotation and that the same holds for the triangles ABD and A"B"D", ABE and A"B"E". But the corresponding sides of these triangles are parallel (for example, AC is parallel to A "C") as the lines of intersection of a certain plane with two parallel planes; it follows that these sides are equal (e.g. AC equals A"C") as opposite sides parallelogram and that the angles formed by these sides are equal and have the same direction.
Definition 2 . A perpendicular section of a prismatic surface is a section of this surface by a plane perpendicular to its edges. Based on the previous theorem, all perpendicular sections of the same prismatic surface will be equal polygons.
Definition 3
. A prism is a polyhedron bounded by a prismatic surface and two planes parallel to each other (but not parallel to the edges of the prismatic surface)
The faces lying in these last planes are called prism bases; faces belonging to a prismatic surface - side faces; edges of the prismatic surface - side edges of the prism. By virtue of the previous theorem, the bases of the prism are equal polygons. All side faces of the prism parallelograms; all side edges are equal to each other.
It is obvious that if the base of the prism ABCDE and one of the edges AA" are given in magnitude and direction, then it is possible to construct a prism by drawing the edges BB", CC", .., equal and parallel to the edge AA".
Definition 4 . The height of a prism is the distance between the planes of its bases (HH").
Definition 5
. A prism is called a straight line if its bases are perpendicular sections of a prismatic surface. In this case, the height of the prism is, of course, its side rib; side edges will rectangles.
Prisms can be classified according to the number of side faces, equal number sides of the polygon that serves as its base. Thus, prisms can be triangular, quadrangular, pentagonal, etc.
Theorem 2
. The area of the lateral surface of the prism is equal to the product of the lateral edge and the perimeter of the perpendicular section.
Let ABCDEA"B"C"D"E" be the given prism and abcde be its perpendicular section, so that the segments ab, bc, .. are perpendicular to its side edges. Face ABA"B" is a parallelogram; its area is equal to the product of the base AA " to a height that matches ab; the area of \u200b\u200bthe face BCV "C" is equal to the product of the base BB" by the height bc, etc. Therefore, the side surface (i.e., the sum of the areas of the side faces) is equal to the product of the side edge, in other words, the total length of the segments AA", BB", .., by the sum ab+bc+cd+de+ea.
Different prisms are different from each other. At the same time, they have a lot in common. To find the area of \u200b\u200bthe base of a prism, you need to figure out what kind it looks like.
General theory
A prism is any polyhedron whose sides have the form of a parallelogram. Moreover, any polyhedron can be at its base - from a triangle to an n-gon. Moreover, the bases of the prism are always equal to each other. What does not apply to the side faces - they can vary significantly in size.
When solving problems, it is not only the area of \u200b\u200bthe base of the prism that is encountered. It may be necessary to know the lateral surface, that is, all faces that are not bases. The full surface will already be the union of all the faces that make up the prism.
Sometimes heights appear in tasks. It is perpendicular to the bases. The diagonal of a polyhedron is a segment that connects in pairs any two vertices that do not belong to the same face.
It should be noted that the area of the base of a straight or inclined prism does not depend on the angle between them and the side faces. If they have the same figures in the upper and lower faces, then their areas will be equal.
triangular prism
It has at the base a figure with three vertices, that is, a triangle. It is known to be different. If then it is enough to recall that its area is determined by half the product of the legs.
Mathematical notation looks like this: S = ½ av.
To find the area of the base in general view, the formulas are useful: Heron and the one in which half of the side is taken to the height drawn to it.
The first formula should be written like this: S \u003d √ (p (p-a) (p-in) (p-s)). This entry contains a semi-perimeter (p), that is, the sum of three sides divided by two.
Second: S = ½ n a * a.
If you want to know the area of the base of a triangular prism, which is regular, then the triangle is equilateral. It has its own formula: S = ¼ a 2 * √3.

quadrangular prism
Its base is any of the known quadrilaterals. It can be a rectangle or a square, a parallelepiped or a rhombus. In each case, in order to calculate the area of \u200b\u200bthe base of the prism, you will need your own formula.
If the base is a rectangle, then its area is determined as follows: S = av, where a, b are the sides of the rectangle.
When it comes to a quadrangular prism, the base area of a regular prism is calculated using the formula for a square. Because it is he who lies at the base. S \u003d a 2.
In the case when the base is a parallelepiped, the following equality will be needed: S \u003d a * n a. It happens that a side of a parallelepiped and one of the angles are given. Then, to calculate the height, you need to use additional formula: n a \u003d b * sin A. Moreover, the angle A is adjacent to the side "b", and the height n and opposite to this corner.
If a rhombus lies at the base of the prism, then the same formula will be needed to determine its area as for a parallelogram (since it is a special case of it). But you can also use this one: S = ½ d 1 d 2. Here d 1 and d 2 are two diagonals of the rhombus.

Regular pentagonal prism
This case involves splitting the polygon into triangles, the areas of which are easier to find out. Although it happens that the figures can be with a different number of vertices.
Since the base of the prism is regular pentagon, then it can be divided into five equilateral triangles. Then the area of \u200b\u200bthe base of the prism is equal to the area of one such triangle (the formula can be seen above), multiplied by five.

Regular hexagonal prism
According to the principle described for a pentagonal prism, it is possible to divide the base hexagon into 6 equilateral triangles. The formula for the area of the base of such a prism is similar to the previous one. Only in it should be multiplied by six.
The formula will look like this: S = 3/2 and 2 * √3.

Tasks
No. 1. A regular straight line is given. Its diagonal is 22 cm, the height of the polyhedron is 14 cm. Calculate the area of \u200b\u200bthe base of the prism and the entire surface.
Solution. The base of a prism is a square, but its side is not known. You can find its value from the diagonal of the square (x), which is related to the diagonal of the prism (d) and its height (n). x 2 \u003d d 2 - n 2. On the other hand, this segment "x" is the hypotenuse in a triangle whose legs are equal to the side of the square. That is, x 2 \u003d a 2 + a 2. Thus, it turns out that a 2 \u003d (d 2 - n 2) / 2.
Substitute the number 22 instead of d, and replace “n” with its value - 14, it turns out that the side of the square is 12 cm. Now it’s easy to find out the base area: 12 * 12 \u003d 144 cm 2.
To find out the area of \u200b\u200bthe entire surface, you need to add twice the value of the base area and quadruple the side. The latter is easy to find by the formula for a rectangle: multiply the height of the polyhedron and the side of the base. That is, 14 and 12, this number will be equal to 168 cm 2. The total surface area of the prism is found to be 960 cm 2 .
Answer. The base area of the prism is 144 cm2. The entire surface - 960 cm 2 .
No. 2. Dana At the base lies a triangle with a side of 6 cm. In this case, the diagonal of the side face is 10 cm. Calculate the areas: the base and the side surface.
Solution. Since the prism is regular, its base is an equilateral triangle. Therefore, its area turns out to be equal to 6 squared times ¼ and the square root of 3. A simple calculation leads to the result: 9√3 cm 2. This is the area of one base of the prism.
All side faces are the same and are rectangles with sides of 6 and 10 cm. To calculate their areas, it is enough to multiply these numbers. Then multiply them by three, because the prism has exactly so many side faces. Then the area of the side surface is wound 180 cm 2 .
Answer. Areas: base - 9√3 cm 2, side surface of the prism - 180 cm 2.
Definition.
This is a hexagon, the bases of which are two equal squares, and the side faces are equal rectangles.
Side rib is the common side of two adjacent side faces
Prism Height is a line segment perpendicular to the bases of the prism
Prism Diagonal- a segment connecting two vertices of the bases that do not belong to the same face
Diagonal plane- a plane that passes through the diagonal of the prism and its side edges
Diagonal section- the boundaries of the intersection of the prism and the diagonal plane. The diagonal section of a regular quadrangular prism is a rectangle
Perpendicular section (orthogonal section)- this is the intersection of a prism and a plane drawn perpendicular to its side edges
Elements of a regular quadrangular prism
The figure shows two regular quadrangular prisms, which are marked with the corresponding letters:
- Bases ABCD and A 1 B 1 C 1 D 1 are equal and parallel to each other
- Side faces AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C and CC 1 D 1 D, each of which is a rectangle
- Lateral surface - the sum of the areas of all the side faces of the prism
- Total surface - the sum of the areas of all bases and side faces (the sum of the area of the side surface and bases)
- Side ribs AA 1 , BB 1 , CC 1 and DD 1 .
- Diagonal B 1 D
- Base diagonal BD
- Diagonal section BB 1 D 1 D
- Perpendicular section A 2 B 2 C 2 D 2 .
Properties of a regular quadrangular prism
- The bases are two equal squares
- The bases are parallel to each other
- The sides are rectangles.
- Side faces are equal to each other
- Side faces are perpendicular to the bases
- Lateral ribs are parallel to each other and equal
- Perpendicular section perpendicular to all side ribs and parallel to the bases
- Perpendicular Section Angles - Right
- The diagonal section of a regular quadrangular prism is a rectangle
- Perpendicular (orthogonal section) parallel to the bases
Formulas for a regular quadrangular prism

Instructions for solving problems
When solving problems on the topic " regular quadrangular prism" implies that:Correct prism- a prism at the base of which lies a regular polygon, and the side edges are perpendicular to the planes of the base. That is, a regular quadrangular prism contains at its base square. (see above the properties of a regular quadrangular prism) Note. This is part of the lesson with tasks in geometry (section solid geometry - prism). Here are the tasks that cause difficulties in solving. If you need to solve a problem in geometry, which is not here - write about it in the forum. To indicate the action of extracting square root symbol is used in problem solving√ .
Task.
In a regular quadrangular prism, the base area is 144 cm 2 and the height is 14 cm. Find the diagonal of the prism and the total surface area.Solution.
A regular quadrilateral is a square.
Accordingly, the side of the base will be equal to
Whence the diagonal of the base of a regular rectangular prism will be equal to
√(12 2 + 12 2 ) = √288 = 12√2
The diagonal of a regular prism forms with the diagonal of the base and the height of the prism right triangle. Accordingly, according to the Pythagorean theorem, the diagonal of a given regular quadrangular prism will be equal to:
√((12√2) 2 + 14 2 ) = 22 cm
Answer: 22 cm
Task
Find the total surface area of a regular quadrangular prism if its diagonal is 5 cm and the diagonal of the side face is 4 cm.Solution.
Since the base of a regular quadrangular prism is a square, then the side of the base (denoted as a) is found by the Pythagorean theorem:
A 2 + a 2 = 5 2
2a 2 = 25
a = √12.5
The height of the side face (denoted as h) will then be equal to:
H 2 + 12.5 \u003d 4 2
h 2 + 12.5 = 16
h 2 \u003d 3.5
h = √3.5
The total surface area will be equal to the sum of the lateral surface area and twice the base area
S = 2a 2 + 4ah
S = 25 + 4√12.5 * √3.5
S = 25 + 4√43.75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S \u003d 25 + 10√7 ≈ 51.46 cm 2.
Answer: 25 + 10√7 ≈ 51.46 cm 2.