Nechť jsou dvě přímky l a m na rovině v kartézském souřadném systému dány obecnými rovnicemi: l: A 1 x + B 1 y + C 1 = 0, m: A 2 x + B 2 y + C 2 = 0

Vektory normál k těmto přímkám: = (A 1 , B 1) - k přímce l,

= (A 2 , B 2) k přímce m.

Nechť j je úhel mezi přímkami l a m.

Protože úhly se vzájemně kolmými stranami jsou buď stejné, nebo se sčítají k p, pak , tj. cos j = .

Takže jsme dokázali následující větu.

Teorém. Nechť j je úhel mezi dvěma přímkami v rovině a tyto přímky nechť jsou dány v kartézském souřadnicovém systému obecnými rovnicemi A 1 x + B 1 y + C 1 = 0 a A 2 x + B 2 y + C 2 = 0. Potom cos j = .

Cvičení.

1) Odvoďte vzorec pro výpočet úhlu mezi čarami, pokud:

(1) obě čáry jsou dány parametricky; (2) obě přímky jsou dány kanonickými rovnicemi; (3) jedna přímka je dána parametricky, druhá přímka – obecnou rovnicí; (4) obě přímky jsou dány rovnicí sklonu.

2) Nechť j je úhel mezi dvěma přímkami v rovině a nechť jsou tyto přímky dány kartézskému souřadnicovému systému rovnicemi y = k 1 x + b 1 a y =k 2 x + b 2 .

Pak tan j =.

3) Prozkoumejte vzájemnou polohu dvou přímek daných obecnými rovnicemi v kartézském souřadnicovém systému a vyplňte tabulku:

Vzdálenost od bodu k přímce v rovině.

Nechť je přímka l v rovině v kartézském souřadném systému dána obecnou rovnicí Ax + By + C = 0. Určete vzdálenost bodu M(x 0 , y 0) k přímce l.

Vzdálenost od bodu M k přímce l je délka kolmice HM (H н l, HM ^ l).

Vektor a normálový vektor k přímce l jsou kolineární, takže | | = | | | | a | | = .

Nechť souřadnice bodu H jsou (x,y).

Protože bod H patří přímce l, pak Ax + By + C = 0 (*).

Souřadnice vektorů a: = (x 0 - x, y 0 - y), = (A, B).

| | = = =

(C = -Ax - By , viz (*))

Teorém. Nechť je přímka l dána v kartézské soustavě souřadnic obecnou rovnicí Ax + By + C = 0. Pak vzdálenost od bodu M(x 0 , y 0) k této přímce vypočteme podle vzorce: r (M; l) = .

Cvičení.

1) Odvoďte vzorec pro výpočet vzdálenosti od bodu k přímce, pokud: (1) přímka je dána parametricky; (2) přímka je dána kanonickými rovnicemi; (3) přímka je dána rovnicí sklonu.

2) Napište rovnici kružnice tečné k přímce 3x - y = 0 se středem Q(-2,4).

3) Napište rovnice přímek rozdělujících úhly, které svírají průsečík přímek 2x + y - 1 = 0 a x + y + 1 = 0 na polovinu.

§ 27. Analytická definice roviny v prostoru

Definice. Normální vektor k rovině budeme nazývat nenulový vektor, jehož libovolný zástupce je kolmý k dané rovině.

Komentář. Je jasné, že pokud je alespoň jeden zástupce vektoru kolmý k rovině, pak všichni ostatní zástupci vektoru jsou kolmí k této rovině.

Nechť je dán kartézský souřadnicový systém v prostoru.

Nechť je dána rovina a, = (A, B, C) – normálový vektor k této rovině, bod M (x 0 , y 0 , z 0) patří rovině a.

Pro libovolný bod N(x, y, z) roviny a jsou vektory a ortogonální, to znamená, že jejich skalární součin je roven nule: = 0. Poslední rovnost zapišme v souřadnicích: A(x - x 0) + B(y - y 0) + C(z - z 0) = 0.

Nechť -Ax 0 - By 0 - Cz 0 = D, pak Ax + By + Cz + D = 0.

Vezměte bod K (x, y) takový, že Ax + By + Cz + D \u003d 0. Protože D \u003d -Ax 0 - By 0 - Cz 0, pak A(x - x 0) + B (y - y 0) + C (z - z 0) = 0. Protože souřadnice orientovaného segmentu = (x - x 0 , y - y 0 , z - z 0), poslední rovnost znamená, že ^ , a tedy K н a.

Takže jsme dokázali následující teorém:

Teorém. Libovolnou rovinu v prostoru v kartézském souřadnicovém systému lze definovat rovnicí ve tvaru Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0), kde (A, B, C) jsou souřadnice normálového vektoru k této rovině.

Opak je také pravdou.

Teorém. Jakákoli rovnice ve tvaru Ax + By + Cz + D \u003d 0 (A 2 + B 2 + C 2 ≠ 0) v kartézském souřadnicovém systému definuje určitou rovinu, zatímco (A, B, C) jsou souřadnice normálového vektoru k této rovině.

Důkaz.

Vezměte bod M (x 0 , y 0 , z 0) takový, že Ax 0 + By 0 + Cz 0 + D = 0 a vektor = (A, B, C) ( ≠ q).

Bodem M kolmým k vektoru prochází rovina (a pouze jedna). Podle předchozí věty je tato rovina dána rovnicí Ax + By + Cz + D = 0.

Definice. Rovnice ve tvaru Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) se nazývá obecná rovnice roviny.

Příklad.

Napišme rovnici roviny procházející body M (0,2,4), N (1,-1,0) a K (-1,0,5).

1. Najděte souřadnice normálového vektoru k rovině (MNK). Protože vektorový produkt´ je ortogonální k nekolineárním vektorům a , pak je vektor kolineární k ´ .

= (1, -3, -4), = (-1, -2, 1);

´ = ,

' = (-11, 3, -5).

Takže jako normální vektor vezměte vektor = (-11, 3, -5).

2. Použijme nyní výsledky první věty:

rovnice dané roviny A(x - x 0) + B(y - y 0) + C(z - z 0) = 0, kde (A, B, C) jsou souřadnice normálového vektoru, (x 0 , y 0, z 0) jsou souřadnice bodu ležícího v rovině (například bodu M).

11 (x - 0) + 3 (y - 2) - 5 (z - 4) = 0

11x + 3y - 5z + 14 = 0

Odpověď: -11x + 3y - 5z + 14 = 0.

Cvičení.

1) Napište rovnici roviny if

(1) rovina prochází bodem M (-2,3,0) rovnoběžně s rovinou 3x + y + z = 0;

(2) rovina obsahuje osu (Ox) a je kolmá k rovině x + 2y – 5z + 7 = 0.

2) Napište rovnici pro rovinu procházející třemi danými body.

§ 28. Analytická specifikace půlprostoru*

Komentář*. Nechte nějaké letadlo opravit. Pod poloprostor budeme chápat množinu bodů ležících na jedné straně dané roviny, to znamená, že dva body leží ve stejném poloprostoru, jestliže úsečka je spojující neprotíná danou rovinu. Tato rovina se nazývá hranice tohoto poloprostoru. Zavolá se spojení dané roviny a poloprostoru uzavřený poloprostor.

Nechť je kartézský souřadnicový systém fixován v prostoru.

Teorém. Nechť je rovina a dána obecnou rovnicí Ax + By + Cz + D = 0. Pak jeden ze dvou poloprostorů, na které rovina a dělí prostor, je dán nerovností Ax + By + Cz + D > 0, a druhý poloprostor je dán nerovností Ax + By + Cz + D< 0.

Důkaz.

Vynesme normálový vektor = (A, B, С) do roviny a z bodu M (x 0 , y 0 , z 0) ležícího v této rovině: = , M н a, MN ^ a. Rovina rozděluje prostor na dva poloprostory: b 1 a b 2 . Je jasné, že bod N patří do jednoho z těchto poloprostorů. Bez ztráty obecnosti předpokládáme, že N н b 1 .

Dokažme, že poloprostor b 1 je definován nerovností Ax + By + Cz + D > 0.

1) Vezměte bod K(x,y,z) v poloprostoru b 1 . Úhel Ð NMK je úhel mezi vektory a je ostrý, takže skalární součin těchto vektorů je kladný: > 0. Zapišme tuto nerovnost v souřadnicích: A(x - x 0) + B(y - y 0) + C(z - z 0) > 0, tedy Ax + By + Cy - Ax 0 - By 0 - C.

Protože M н b 1, pak Ax 0 + By 0 + C z 0 + D = 0, tedy -Ax 0 - By 0 - C z 0 = D. Poslední nerovnost lze tedy zapsat takto: Ax + By + Cz + D > 0.

2) Vezměte bod L(x,y) takový, že Ax + By + Cz + D > 0.

Přepišme nerovnost tak, že D nahradíme (-Ax 0 - By 0 - C z 0) (protože M н b 1, pak Ax 0 + By 0 + C z 0 + D = 0): A(x - x 0) + B(y - y 0) + C(z - z 0) > 0.

Vektor se souřadnicemi (x - x 0, y - y 0, z - z 0) je vektor, takže výraz A(x - x 0) + B(y - y 0) + C(z - z 0) lze chápat jako skalární součin vektorů a . Protože skalární součin vektorů a je kladný, úhel mezi nimi je ostrý a bod L н b 1 .

Podobně lze dokázat, že poloprostor b 2 je dán nerovností Ax + By + Cz + D< 0.

Poznámky.

1) Je zřejmé, že výše uvedený důkaz nezávisí na volbě bodu M v rovině a.

2) Je jasné, že stejný poloprostor lze definovat různými nerovnostmi.

Opak je také pravdou.

Teorém. Libovolná lineární nerovnost tvaru Ax + By + Cz + D > 0 (nebo Ax + By + Cz + D< 0) (A 2 + B 2 + C 2 ≠ 0) задает в пространстве в декартовой системе координат полупространство с границей Ax + By + Cz + D = 0.

Důkaz.

Rovnice Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) v prostoru definuje nějakou rovinu a (viz § ...). Jak bylo prokázáno v předchozí větě, jeden ze dvou poloprostorů, na které rovina rozděluje prostor, je dán nerovností Ax Ax + By + Cz + D > 0.

Poznámky.

1) Je jasné, že uzavřený poloprostor lze definovat nepřísnou lineární nerovností a jakákoli nepřísná lineární nerovnost v kartézském souřadnicovém systému definuje uzavřený poloprostor.

2) Libovolný konvexní mnohostěn lze definovat jako průsečík uzavřených poloprostorů (jejichž hranicemi jsou roviny obsahující plochy mnohostěnu), tedy analyticky systémem lineárních nepřísných nerovností.

Cvičení.

1) Dokažte dvě uvedené věty pro libovolný afinní systém souřadnice.

2) Je naopak pravdou, že jakýkoli systém není přísný lineární nerovnosti definuje konvexní mnohoúhelník?

Cvičení.

1) Prozkoumejte vzájemnou polohu dvou rovin danou obecnými rovnicemi v kartézském souřadnicovém systému a vyplňte tabulku.

ÚHEL MEZI ROVINAMI

Uvažujme dvě roviny α 1 a α 2 dané rovnicemi:

Pod roh mezi dvěma rovinami rozumíme jeden z dihedrálních úhlů tvořených těmito rovinami. Je zřejmé, že úhel mezi normálovými vektory a rovinami α 1 a α 2 je roven jednomu z naznačených sousedních dihedrálních úhlů popř. . Proto . Protože A , Že

.

Příklad. Určete úhel mezi rovinami X+2y-3z+4=0 a 2 X+3y+z+8=0.

Podmínka rovnoběžnosti dvou rovin.

Dvě roviny α 1 a α 2 jsou rovnoběžné právě tehdy, když jejich normálové vektory a jsou rovnoběžné, a proto .

Dvě roviny jsou tedy navzájem rovnoběžné právě tehdy, když jsou koeficienty na odpovídajících souřadnicích úměrné:

nebo

Podmínka kolmosti rovin.

Je jasné, že dvě roviny jsou kolmé právě tehdy, když jsou jejich normálové vektory kolmé, a proto, nebo .

Tím pádem, .

Příklady.

PŘÍMO V PROSTORU.

VEKTOROVÁ ROVNICE PŘÍMÁ.

PARAMETRICKÉ ROVNICE PŘÍMÉ

Poloha přímky v prostoru je zcela určena určením kteréhokoli z jejích pevných bodů M 1 a vektor rovnoběžný s touto přímkou.

Nazývá se vektor rovnoběžný s přímkou vedení vektor této čáry.

Nechte tedy rovnou l prochází bodem M 1 (X 1 , y 1 , z 1) ležící na přímce rovnoběžné s vektorem .

Zvažte libovolný bod M(x,y,z) na přímce. Z obrázku je to vidět .

Vektory a jsou kolineární, takže existuje takové číslo t, co , kde je násobitel t může nabývat libovolné číselné hodnoty v závislosti na poloze bodu M na přímce. Faktor t se nazývá parametr. Označení poloměrových vektorů bodů M 1 a M respektive prostřednictvím a , získáme . Tato rovnice se nazývá vektor rovnice přímky. Ukazuje, že hodnota každého parametru t odpovídá vektoru poloměru nějakého bodu M ležící na přímce.

Tuto rovnici zapíšeme v souřadnicovém tvaru. Všimněte si, že, a odtud

Výsledné rovnice se nazývají parametrické přímkové rovnice.

Při změně parametru t změna souřadnic X, y A z a tečka M se pohybuje v přímé linii.

KANONICKÉ ROVNICE PŘÍMÉ

Nechat M 1 (X 1 , y 1 , z 1) - bod ležící na přímce l, A je jeho směrový vektor. Opět vezměte libovolný bod na přímce M(x,y,z) a zvažte vektor .

Je jasné, že vektory a jsou kolineární, takže jejich příslušné souřadnice musí být proporcionální

– kanonický přímkové rovnice.

Poznámka 1. Všimněte si, že kanonické rovnice přímky lze získat z parametrických rovnic odstraněním parametru t. Ve skutečnosti z parametrických rovnic, které získáme nebo .

Příklad. Napište rovnici přímky parametrickým způsobem.

Označit , tedy X = 2 + 3t, y = –1 + 2t, z = 1 –t.

Poznámka 2. Nechť je čára kolmá k jedné ze souřadnicových os, například k ose Vůl. Potom je směrový vektor přímky kolmý Vůl, tedy, m=0. V důsledku toho mají parametrické rovnice přímky tvar

Vyloučení parametru z rovnic t, získáme rovnice přímky ve tvaru

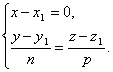
I v tomto případě však souhlasíme s formálním zápisem kanonických rovnic přímky do formuláře . Pokud je tedy jmenovatel jednoho ze zlomků nula, znamená to, že přímka je kolmá k příslušné souřadnicové ose.

Podobně kanonické rovnice odpovídá přímce kolmé k osám Vůl A Oj nebo rovnoběžná osa Oz.

Příklady.

OBECNÉ ROVNICE PŘÍMÁ ČÁRA JAKO ČÁRA ZÁJMU DVOU ROVIN

Každou přímkou ​​v prostoru prochází nekonečný počet rovin. Jakékoli dva z nich, které se protínají, jej definují v prostoru. Proto rovnice jakýchkoli dvou takových rovin, uvažované společně, jsou rovnicemi této přímky.

Obecně jakékoli dvě nerovnoběžné roviny dané obecnými rovnicemi

určit jejich průsečík. Tyto rovnice se nazývají obecné rovnice rovný.

Příklady.

Sestrojte přímku danou rovnicí

K sestrojení úsečky stačí najít libovolné dva její body. Nejjednodušší způsob je vybrat průsečíky přímky s souřadnicové roviny. Například průsečík s rovinou xOy získáme z rovnic přímky, za předpokladu z= 0:

Při řešení tohoto systému nacházíme pointu M 1 (1;2;0).

Podobně za předpokladu y= 0, dostaneme průsečík přímky s rovinou xOz:

Od obecných rovnic přímky lze přejít k jejím kanonickým nebo parametrickým rovnicím. Chcete-li to provést, musíte najít nějaký bod M 1 na přímce a směrový vektor přímky.

Souřadnice bodu M 1 získáme z tohoto systému rovnic, přičemž jedné ze souřadnic přiřadíme libovolnou hodnotu. Chcete-li najít směrový vektor, poznamenejte si, že tento vektor musí být kolmý k oběma normálovým vektorům A . Tedy pro směrový vektor přímky l můžete vzít křížový součin normálních vektorů:

.

Příklad. Uveďte obecné rovnice přímky na kanonickou formu.

Najděte bod na přímce. K tomu zvolíme libovolně jednu ze souřadnic, např. y= 0 a vyřeš soustavu rovnic:

Normální vektory rovin definujících přímku mají souřadnice Proto bude směrový vektor přímý

. Proto, l: .

ÚHEL MEZI PRÁVA

roh mezi přímkami v prostoru budeme nazývat libovolný ze sousedních úhlů tvořených dvěma přímkami vedenými libovolným bodem rovnoběžným s daty.

Nechť jsou v prostoru uvedeny dvě rovné čáry:

Je zřejmé, že úhel φ mezi čarami lze brát jako úhel mezi jejich směrovými vektory a . Od , pak podle vzorce pro kosinus úhlu mezi vektory dostaneme

Pro každého studenta, který se připravuje na zkoušku z matematiky, bude užitečné zopakovat si téma „Hledání úhlu mezi čarami“. Jak ukazují statistiky, při absolvování atestačního testu působí úlohy z tohoto úseku stereometrie velkému počtu studentů potíže. Úlohy vyžadující nalezení úhlu mezi přímkami se přitom v USE nacházejí jak základní, tak i úroveň profilu. To znamená, že by je měl umět vyřešit každý.

Základní momenty

Existují 4 typy vzájemného uspořádání čar v prostoru. Mohou se shodovat, protínat, být rovnoběžné nebo protínající se. Úhel mezi nimi může být ostrý nebo přímý.

K nalezení úhlu mezi čarami v Jednotné státní zkoušce nebo například v řešení mohou školáci v Moskvě a dalších městech použít několik metod řešení problémů v této části stereometrie. Úkol můžete splnit klasickými konstrukcemi. K tomu se vyplatí naučit se základní axiomy a věty stereometrie. Student musí být schopen logicky budovat uvažování a vytvářet výkresy, aby přivedl úlohu k planimetrickému problému.

Můžete také použít metodu vektorových souřadnic aplikací jednoduché vzorce, pravidla a algoritmy. Hlavní věcí v tomto případě je správně provést všechny výpočty. Zdokonalte své dovednosti při řešení problémů ve stereometrii a dalších tématech školní kurz pomůžu ti vzdělávací projekt"Školkovo".

Nechť čáry jsou uvedeny v prostoru l A m. Přes nějaký bod A prostoru vedeme rovné čáry l 1 || l A m 1 || m(obr. 138).

Všimněte si, že bod A může být zvolen libovolně, zejména může ležet na jedné z uvedených přímek. Pokud rovnou l A m protínají, pak lze A považovat za průsečík těchto čar ( l 1 = l A m 1 = m).

Úhel mezi nerovnoběžnými čarami l A m je hodnota nejmenšího ze sousedních úhlů vytvořených protínajícími se přímkami l 1 A m 1 (l 1 || l, m 1 || m). Předpokládá se, že úhel mezi rovnoběžnými čarami je nulový.

Úhel mezi čarami l A m označeno \(\widehat((l;m)) \). Z definice vyplývá, že pokud se měří ve stupních, pak 0 ° < \(\widehat((l;m)) \) < 90°, a pokud v radiánech, pak 0 < \(\widehat((l;m)) \) < π / 2 .

Úkol. Je dána krychle ABCDA 1 B 1 C 1 D 1 (obr. 139).

Najděte úhel mezi přímkami AB a DC 1 .

Přímá křižovatka AB a DC 1. Protože přímka DC je rovnoběžná s přímkou ​​AB, úhel mezi přímkami AB a DC 1 je podle definice roven \(\widehat(C_(1)DC)\).

Proto \(\widehat((AB;DC_1))\) = 45°.

Přímo l A m volal kolmý, jestliže \(\widehat((l;m)) \) = π / 2. Například v krychli

Výpočet úhlu mezi čarami.

Problém výpočtu úhlu mezi dvěma přímkami v prostoru je řešen stejně jako v rovině. Označme φ úhel mezi úsečkami l 1 A l 2 a skrz ψ - úhel mezi směrovými vektory A A b tyto rovné čáry.

Pak kdyby

ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (obr. 206.6), pak φ = 180° - ψ. Je zřejmé, že v obou případech platí rovnost cos φ = |cos ψ|. Podle vzorce (kosinus úhlu mezi nenulovými vektory a a b se rovná skalárnímu součinu těchto vektorů dělenému součinem jejich délek) máme

$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$

proto,

$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$

Nechť jsou přímky dány jejich kanonickými rovnicemi

$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; A \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$

Potom se pomocí vzorce určí úhel φ mezi přímkami

$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2)\sqrt((b_1)^2+(b_2)^2+)(b_1)

Pokud je jedna z přímek (nebo obě) dána nekanonickými rovnicemi, pak pro výpočet úhlu musíte najít souřadnice směrových vektorů těchto přímek a poté použít vzorec (1).

Úkol 1. Vypočítejte úhel mezi čarami

$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;and\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$

Směrové vektory přímek mají souřadnice:

a \u003d (-√2; √2; -2), b = (√3 ; √3 ; √6 ).

Podle vzorce (1) najdeme

$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)(2\sqrt2\cdot 2\sqrt3)=\frac(1)(2)

Proto je úhel mezi těmito čarami 60°.

Úkol 2. Vypočítejte úhel mezi čarami

$$ \begin(cases)3x-12z+7=0\\x+y-3z-1=0\end(cases) and \begin(cases)4x-y+z=0\\y+z+1=0\end(cases) $$

Za vodicím vektorem A první přímka vezmeme vektorový součin normálových vektorů n 1 = (3; 0; -12) a n 2 = (1; 1; -3) roviny definující tuto přímku. Podle vzorce \(=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) \) dostaneme

$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$

Podobně najdeme směrový vektor druhé přímky:

$$ b=\začátek(vmatice) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatice)=-2i-4i+4k $$

Ale vzorec (1) vypočítá kosinus požadovaného úhlu:

$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2^2+4^2+4^2))=0 $$

Proto je úhel mezi těmito čarami 90°.

Úkol 3. V trojúhelníkovém jehlanu MAVS jsou hrany MA, MB a MC vzájemně kolmé, (obr. 207);

jejich délky se rovnají 4, 3, 6. Bod D je střed [MA]. Najděte úhel φ mezi přímkami CA a DB.

Nechť SA a DB jsou směrové vektory přímek SA a DB.

Vezměme bod M jako počátek souřadnic. Podle podmínky úlohy máme A (4; 0; 0), B(0; 0; 3), C(0; 6; 0), D (2; 0; 0). Proto \(\overrightarrow(CA)\) = (4; - 6;0), \(\overrightarrow(DB)\)= (-2; 0; 3). Použijeme vzorec (1):

$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9)) $$

Podle tabulky kosinů zjistíme, že úhel mezi přímkami CA a DB je přibližně 72°.

S pomocí tohoto online kalkulačka najít úhel mezi čarami. Je uvedeno podrobné řešení s vysvětlením. Pro výpočet úhlu mezi čarami nastavte kótu (2-pokud se uvažuje přímka v rovině, 3- pokud se uvažuje přímka v prostoru), do buněk zadejte prvky rovnice a klikněte na tlačítko "Vyřešit". Viz teoretická část níže.

×

Varování

Vymazat všechny buňky?

Zavřít Vymazat

Instrukce pro zadávání dat.Čísla se zadávají jako celá čísla (příklady: 487, 5, -7623 atd.), desetinná čísla (např. 67., 102,54 atd.) nebo zlomky. Zlomek musí být zadán ve tvaru a/b, kde a a b (b>0) jsou celá čísla resp. desetinná čísla. Příklady 45/5, 6,6/76,4, -7/6,7 atd.

1. Úhel mezi přímkami v rovině

Přímky jsou dány kanonickými rovnicemi

1.1. Určení úhlu mezi čarami

Nechte čáry ve dvourozměrném prostoru L 1 a L

Ze vzorce (1.4) lze tedy zjistit úhel mezi čarami L 1 a L 2. Jak je vidět z obr. 1, protínající se čáry svírají sousední úhly φ A φ 1. Pokud je nalezený úhel větší než 90°, můžete najít minimální úhel mezi čarami L 1 a L 2: φ 1 =180-φ .

Ze vzorce (1.4) lze odvodit podmínky rovnoběžnosti a kolmosti dvou přímek.

Příklad 1. Určete úhel mezi úsečkami

Pojďme to zjednodušit a vyřešit:

1.2. Stav rovnoběžných čar

Nechat φ =0. Pak cosφ=1. V tomto případě bude mít výraz (1.4) následující tvar:

,

,

Příklad 2. Určete, zda jsou přímky rovnoběžné

Rovnost (1.9) je splněna, proto jsou přímky (1.10) a (1.11) rovnoběžné.

Odpovědět. Přímky (1.10) a (1.11) jsou rovnoběžné.

1.3. Podmínka kolmosti čar

Nechat φ = 90°. Pak cosφ=0. V tomto případě bude mít výraz (1.4) následující tvar:

Příklad 3. Určete, zda jsou čáry kolmé

Podmínka (1.13) je splněna, přímky (1.14) a (1.15) jsou tedy kolmé.

Odpovědět. Čáry (1.14) a (1.15) jsou kolmé.

Přímky jsou dány obecnými rovnicemi

1.4. Určení úhlu mezi čarami

Nechte dva řádky L 1 a L 2 jsou dány obecnými rovnicemi

Z definice skalárního součinu dvou vektorů máme:

Příklad 4. Najděte úhel mezi čarami

Dosazování hodnot A 1 , B 1 , A 2 , B 2 palce (1,23), dostaneme:

Tento úhel je větší než 90°. Najděte minimální úhel mezi čarami. Chcete-li to provést, odečtěte tento úhel od 180:

Na druhou stranu podmínka rovnoběžných čar L 1 a L 2 je ekvivalentní podmínce kolineárních vektorů n 1 a n 2 a může být znázorněn takto:

Rovnost (1.24) je splněna, proto jsou přímky (1.26) a (1.27) rovnoběžné.

Odpovědět. Přímky (1.26) a (1.27) jsou rovnoběžné.

1.6. Podmínka kolmosti čar

Podmínka kolmosti čar L 1 a L 2 lze získat ze vzorce (1.20) substitucí cos(φ )=0. Poté skalární součin ( n 1 ,n 2) = 0. Kde

Rovnost (1.28) je splněna, přímky (1.29) a (1.30) jsou tedy kolmé.

Odpovědět. Čáry (1.29) a (1.30) jsou kolmé.

2. Úhel mezi čarami v prostoru

2.1. Určení úhlu mezi čarami

Nechte čáry v prostoru L 1 a L 2 jsou dány kanonickými rovnicemi

kde | q 1 | a | q 2 | směrové vektorové moduly q 1 a q 2 resp. φ -úhel mezi vektory q 1 a q 2 .

Z výrazu (2.3) dostaneme:

.

Pojďme to zjednodušit a vyřešit:

.

Pojďme najít roh φ