Použití křížového produktu VEKTORŮ

pro výpočet plochy

nějaký geometrické tvary

Výzkum matematika

Žák 10 B tř

MOU střední škola №73

Michail Perevoznikov

Vedoucí:

Učitelka matematiky MOU střední škola №73 Dragunova Svetlana Nikolaevna

Asistentka oddělení. matematická analýza Fakulta mechaniky a matematiky SSU N.G. Černyševskij Berdnikov Gleb Sergejevič

Saratov, 2015

Úvod.

1. Teoretický přehled.

1.1. Vektory a výpočty s vektory.

1.2. Využití skalárního součinu vektorů při řešení úloh

1.3 Bodový součin vektorů v souřadnicích

1.4. Vektorový součin vektorů v trojrozměrném euklidovském prostoru: definice pojmu.

1.5. Vektorové souřadnice produkty vektorů.

2. Praktická část.

2.1. Vztah mezi křížovým produktem a plochou trojúhelníku a rovnoběžníku. Odvození vzorce a geometrický význam vektorového součinu vektorů.

2.2. Pokud znáte pouze souřadnice bodů, najděte oblast trojúhelníku. Důkaz věty

2.3. Kontrola na příkladech správnosti vzorce.

2.4. Praktické využití vektorové algebry a součinu vektorů.

Závěr

Úvod

Jak víte, mnoho geometrických problémů má dvě klíčová řešení – grafické a analytické. Grafická metoda je spojena s konstrukcí grafů a kreseb a analytická metoda zahrnuje řešení problémů především pomocí algebraické operace. V druhém případě souvisí algoritmus řešení problémů s analytickou geometrií. Analytická geometrie je obor matematiky, respektive lineární algebry, který uvažuje o řešení geometrických problémů pomocí algebry na základě metody souřadnic v rovině a v prostoru. Analytická geometrie umožňuje analyzovat geometrické obrazy, zkoumat linie a povrchy, které jsou důležité pro praktické aplikace. Navíc v této vědě, aby se rozšířilo prostorové chápání obrazců, se navíc někdy používá vektorový součin vektorů.

Vzhledem k rozšířenému používání trojrozměrných prostorových technologií se jako relevantní jeví studium vlastností některých geometrických tvarů pomocí vektorového součinu.

V tomto ohledu byl identifikován účel tohoto projektu - použití křížového součinu vektorů pro výpočet plochy některých geometrických tvarů.

V souvislosti s tímto cílem byly řešeny následující úkoly:

1. Teoreticky studovat nezbytné základy vektorové algebry a definovat vektorový součin vektorů v souřadnicovém systému;

2. Analyzujte přítomnost spojení mezi vektorovým součinem a oblastí trojúhelníku a rovnoběžníku;

3. Odvoďte vzorec pro oblast trojúhelníku a rovnoběžníku v souřadnicích;

4. Zkontrolujte konkrétní příklady správnost odvozeného vzorce.

1. Teoretický přehled.

1. Vektory a výpočty s vektory

Vektor je směrovaný segment, pro který je uveden jeho začátek a konec:

V tomto případě je bodem začátek segmentu A, konec segmentu je bod V. Samotný vektor je označen
nebo . Chcete-li najít souřadnice vektoru
, když známe souřadnice jeho počátečních bodů A a koncového bodu B, je nutné odečíst odpovídající souřadnice počátečního bodu od souřadnic koncového bodu:

= { B X -A X ; B y -A y }

Vektory, které leží na rovnoběžných čarách nebo na stejné přímce, se nazývají kolineární. V tomto případě je vektorem segment charakterizovaný délkou a směrem.

Délka orientovaného segmentu určuje číselnou hodnotu vektoru a nazývá se délka vektoru nebo modul vektoru.

Délka vektoru || v obdélníkovém Kartézské souřadnice je rovný odmocnina ze součtu druhých mocnin jeho souřadnic.

S vektory to zvládnete různé aktivity.

Například sčítání. Chcete-li je přidat, musíte nejprve nakreslit druhý vektor od konce prvního a poté spojit začátek prvního s koncem druhého (obr. 1). Součet vektorů je další vektor s novými souřadnicemi.

Součet vektorů = {A X ; A y) A = {b X ; b y) lze nalézt pomocí následujícího vzorce:

+ = (a X +b X ; A y +b y }

Rýže. 1. Akce s vektory

Při odečítání vektorů je musíte nejprve nakreslit z jednoho bodu a poté připojit konec druhého ke konci prvního.

Vektorový rozdíl = {A X ; A y) A = {b X ; b y } lze najít pomocí vzorce:

- = { A X -b X ; A y -b y }

Také vektory lze násobit číslem. Výsledkem bude také vektor, který je kkrát větší (nebo menší) než daný. Jeho směr bude záviset na znaménku k: je-li k kladné, vektory jsou ve stejném směru, a je-li k záporné, směřují opačně.

Vektorový produkt = {A X ; A y } a číslo k lze najít pomocí následujícího vzorce:

k = (k A X ; k a y }

Je možné vynásobit vektor vektorem? Samozřejmě, a dokonce dvě možnosti!

První možností je skalární součin.

Rýže. 2. Bodový součin v souřadnicích

K nalezení součinu vektorů můžete použít úhel  mezi těmito vektory, jak je znázorněno na obrázku 3.

Ze vzorce vyplývá, že skalární součin je roven součinu délek těchto vektorů a kosinu úhlu mezi nimi, jeho výsledkem je číslo. Je důležité, že pokud jsou vektory kolmé, pak je jejich skalární součin roven nule, protože kosinus pravý úhel mezi nimi je nula.

V souřadnicová rovina vektor má také souřadnice. V vektory, jejich souřadnice a bodový součin jsou jedny z nejpohodlnějších metod pro výpočet úhlu mezi čarami (nebo jejich segmenty), pokud je zadán souřadnicový systém.A pokud souřadnice
, pak jejich skalární součin je:

V trojrozměrném prostoru existují 3 osy, a proto body a vektory v takovém systému budou mít každý 3 souřadnice a skalární součin vektorů se vypočítá podle vzorce:

1.2. Vektorový součin vektorů v trojrozměrném prostoru.

Druhou možností pro výpočet součinu vektorů je vektorový součin. Abychom to ale mohli určit, už není potřeba rovina, ale trojrozměrný prostor, ve kterém má začátek a konec vektoru každý 3 souřadnice.

Na rozdíl od skalárního součinu vektorů v trojrozměrném prostoru vede operace „násobení vektorů“ na vektorech k jinému výsledku. Jestliže v předchozím případě skalárního násobení dvou vektorů bylo výsledkem číslo, pak v případě vektorového násobení vektorů bude výsledkem další vektor kolmý na oba vektory, které vstoupily do součinu. Proto se tento součin vektorů nazývá vektorový součin.

Pochopitelně při konstrukci výsledného vektoru , kolmo ke dvěma, které vstoupily do produktu - a , lze zvolit dva opačné směry. V tomto případě směr výsledného vektoru je určeno pravidlem pravé ruky nebo pravidlem gimlet. Pokud nakreslíte vektory tak, aby se jejich počátky shodovaly a otočíte první vektor násobiče nejkratší cestou k vektoru druhého násobiče a čtyři prsty pravé ruky ukazují směr otáčení (jako by objímaly rotující válec), pak vyčnívající palec ukáže směr vektoru součinu7 (obr.

Rýže. 7. Pravidlo pravé ruky

1.3. Vlastnosti křížového součinu vektorů.

Délka výsledného vektoru je určena vzorcem

.

V čem
vektorový produkt. Jak bylo uvedeno výše, výsledný vektor bude kolmý
a jeho směr je určen pravidlem pravé ruky.

Vektorový součin závisí na pořadí faktorů, konkrétně:

Křížový součin nenulových vektorů je 0, pokud jsou kolineární, pak sinus úhlu mezi nimi bude 0.

Souřadnice vektorů v trojrozměrném prostoru jsou vyjádřeny takto: . Potom se podle vzorce zjistí souřadnice výsledného vektoru

Délku výsledného vektoru zjistíme podle vzorce:

.

2. Praktická část.

2.1. Spojení vektorového produktu s plochou trojúhelníku a rovnoběžníku v rovině. Geometrický význam křížového součinu vektorů.

Dostaneme trojúhelník ABC (obr. 8). Je známo že .

Pokud znázorníme strany trojúhelníku AB a AC jako dva vektory, pak ve vzorci oblasti trojúhelníku najdeme výraz pro křížový součin vektorů:

Z výše uvedeného můžeme určit geometrický význam vektorového součinu (obr. 9):

délka křížového součinu vektorů se rovná dvojnásobku plochy trojúhelníku se stranami vektorů a , pokud jsou odsazeny od jednoho bodu.

Jinými slovy, délka křížového součinu vektorů a je rovna oblast rovnoběžníku, postavené na vektorech A , se stranami a a úhel mezi nimi rovný .

Rýže. 9. Geometrický význam vektorového součinu vektorů

V tomto ohledu můžeme uvést další definici vektorového součinu vektorů :

Křížový součin vektoru na vektoru se nazývá vektor , jehož délka se číselně rovná ploše rovnoběžníku postaveného na vektorech a , kolmé k rovině těchto vektorů a nasměrované tak, aby nejmenší rotace od k kolem vektoru byla provedena proti směru hodinových ručiček při pohledu od konce vektoru (obr. 10).

Rýže. 10. Definice křížového součinu vektorů

pomocí rovnoběžníku

2.2. Odvození vzorce pro nalezení oblasti trojúhelníku v souřadnicích.

Dostaneme tedy trojúhelník ABC v rovině a souřadnice jeho vrcholů. Pojďme najít oblast tohoto trojúhelníku (obr. 11).

Rýže. 11. Příklad řešení problému nalezení oblasti trojúhelníku podle souřadnic jeho vrcholů

Řešení.

Nejprve zvažte souřadnice vrcholů v prostoru a vypočítejte souřadnice vektorů AB a AC.

Podle výše uvedeného vzorce vypočítáme souřadnice jejich vektorového součinu. Délka tohoto vektoru se rovná 2 plochám trojúhelníku ABC. Plocha trojúhelníku je 10.

Navíc, pokud uvažujeme trojúhelník v rovině, pak první 2 souřadnice vektorového součinu budou vždy nulové, takže můžeme formulovat následující větu.

Věta: Nechť je dán trojúhelník ABC a souřadnice jeho vrcholů (obr. 12).

Pak .

Rýže. 12. Důkaz věty

Důkaz.

Uvažujte body v prostoru a vypočítejte souřadnice vektorů BC a BA. . Pomocí výše uvedeného vzorce vypočítáme souřadnice křížového součinu těchto vektorů. Všimněte si, že všechny termíny obsahujícíz 1 nebo z 2 se rovnají 0, protože z 1i z 2 = 0. ODSTRANIT!!!

tak tedy,

2.3. Kontrola správnosti vzorce na příkladech

Najděte oblast trojúhelníku tvořeného vektory a = (-1; 2; -2) a b = (2; 1; -1).

Řešení: Pojďme najít křížový součin těchto vektorů:

A ×b=

I(2 (-1) - (-2) 1) - j((-1) (-1) - (-2) 2) + k((-1) 1 - 2 2) =

I(-2 + 2) - j(1 + 4) + k(-1 - 4) = -5 j - 5 k = (0; -5; -5)

Z vlastností vektorového produktu:

SΔ =

| a×b| =

√ 02 + 52 + 52 =

√ 25 + 25 =

√ 50 =

5√ 2

Odpověď: SΔ = 2,5√2.

Závěr

2.4. Aplikace vektorové algebry

a skalární a křížový součin vektorů.

Kde jsou potřebné vektory? Vektorový prostor a vektory nejsou jen teoretické, ale mají také velmi reálné praktické aplikace moderní svět.

V mechanice a fyzice má mnoho veličin nejen číselnou hodnotu, ale také směr. Takové veličiny se nazývají vektorové veličiny. Spolu s využitím elementárních mechanických pojmů, spoléhání se na jejich fyzický význam, mnoho veličin je považováno za posuvné vektory a jejich vlastnosti jsou popsány jak axiomy, jak je v teoretické mechanice zvykem, tak pomocí tzv. matematické vlastnosti vektory. Nejvýraznější příklady vektorové veličiny jsou rychlost, hybnost a síla (obr. 12). Například moment hybnosti a Lorentzova síla jsou matematicky zapsány pomocí vektorů.

Ve fyzice jsou důležité nejen samotné vektory, ale do značné míry jsou důležité i jejich produkty, které pomáhají vypočítat některé veličiny. Křížový součin je užitečný pro určování kolinearity vektorů. Modul křížového součinu dvou vektorů je roven součinu jejich modulů, pokud jsou kolmé, a klesá na nulu, jsou-li vektory ve společném nebo opačném směru.

Jako další příklad je bodový součin použit k výpočtu práce pomocí níže uvedeného vzorce, kde F je vektor síly a s je vektor posunutí.

Jedním příkladem použití součinu vektorů je moment síly, který se rovná součinu vektoru poloměru nakresleného od osy otáčení k bodu působení síly a vektoru této síly.

Mnoho z toho, co se ve fyzice počítá podle pravidla pravé ruky, je křížový produkt. Najděte důkazy, uveďte příklady.

Za zmínku také stojí, že možné varianty vektorových prostorů nejsou omezeny na dvourozměrný a trojrozměrný prostor. Vyšší matematika uvažuje o prostorech vyšších dimenzí, ve kterých jsou také definovány analogy vzorců pro skalární a vektorový součin. Navzdory skutečnosti, že prostory větších rozměrů než 3 si lidská mysl nedokáže představit, překvapivě nacházejí uplatnění v mnoha oblastech vědy a průmyslu.

Výsledkem křížového součinu vektorů v trojrozměrném euklidovském prostoru přitom není číslo, ale výsledný vektor s vlastními souřadnicemi, směrem a délkou.

Směr výsledného vektoru je určen pravidlem pravé ruky, což je jedno z nejpřekvapivějších ustanovení analytické geometrie.

Křížový součin vektorů lze použít při hledání oblasti trojúhelníku nebo rovnoběžníku daných souřadnicemi vrcholů, což bylo potvrzeno odvozením vzorce, prokázáním věty a řešením praktické úkoly.

Vektory jsou široce používány ve fyzice, kde takové indikátory jako rychlost, hybnost a síla mohou být reprezentovány jako vektorové veličiny a vypočítány geometricky.

Seznam použitých zdrojů

Atanasyan L. S., Butuzov V. F., Kadomtsev S. B. a kol., Geometrie. Ročníky 7-9: učebnice pro vzdělávací organizace. M.: , 2013. 383 s.

Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. et al. Geometrie. Ročníky 10-11: učebnice pro vzdělávací organizace: základní a úrovně profilu. M.: , 2013. 255 s.

Bugrov Ya.S., Nikolsky S.M. Algebra pro pokročilé. První díl: Prvky lineární algebry a analytické geometrie.

Kleteník D.V. Sbírka úloh z analytické geometrie. Moskva: Nauka, Fizmatlit, 1998.

Analytická geometrie.

Matematika. Jetel.

Výuka matematiky online.

http://ru.onlinemschool.com/math/library/vector/multiply1/

Webové stránky V. Glazneva.

http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm

Wikipedie.

https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED%E8%E5

Je zřejmé, že v případě křížového produktu záleží na pořadí, ve kterém jsou vektory přijímány, navíc,

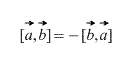
Také přímo z definice vyplývá, že pro jakýkoli skalární faktor k (číslo) platí následující:

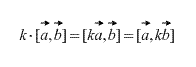
Křížový součin kolineárních vektorů se rovná nulovému vektoru. Kromě toho je křížový součin dvou vektorů nulový právě tehdy, když jsou kolineární. (V případě, že jeden z nich je nulový vektor, je nutné pamatovat na to, že nulový vektor je podle definice kolineární s libovolným vektorem).

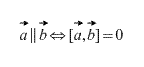
Vektorový produkt má distribuční vlastnictví, to je

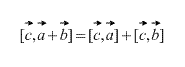
Vyjádření křížového součinu pomocí souřadnic vektorů.

Nechť jsou dány dva vektory

(jak zjistit souřadnice vektoru podle souřadnic jeho začátku a konce - viz článek Bodový součin vektorů, odstavec Alternativní definice bodového součinu aneb výpočet bodového součinu dvou vektorů daného jejich souřadnicemi.)

Proč potřebujete vektorový produkt?

Existuje mnoho způsobů, jak použít křížový součin, například jak již bylo napsáno výše, výpočtem křížového součinu dvou vektorů můžete zjistit, zda jsou kolineární.

Nebo jej lze použít jako způsob výpočtu plochy rovnoběžníku postaveného z těchto vektorů. Na základě definice je délka výsledného vektoru plocha tohoto rovnoběžníku.

Také existuje obrovské množství aplikací v elektřině a magnetismu.

Online kalkulačka vektorového produktu.

Chcete-li pomocí této kalkulačky najít skalární součin dvou vektorů, musíte do prvního řádku zadat souřadnice prvního vektoru v druhý - druhý. Souřadnice vektorů lze vypočítat z jejich počátečních a koncových souřadnic (viz článek Bodový součin vektorů , položka Alternativní definice bodového součinu nebo výpočet bodového součinu dvou vektorů zadaných jejich souřadnicemi.)

Úhel mezi vektory

Abychom mohli zavést pojem křížového součinu dvou vektorů, musíme se nejprve zabývat takovým pojmem, jako je úhel mezi těmito vektory.

Dostaneme dva vektory $\overline(α)$ a $\overline(β)$. Vezmeme nějaký bod $O$ v prostoru a odložíme z něj vektory $\overline(α)=\overline(OA)$ a $\overline(β)=\overline(OB)$, pak úhel $AOB$ budeme nazývat úhel mezi těmito vektory (obr. 1).

Zápis: $∠(\overline(α),\overline(β))$

Koncept křížového součinu vektorů a vzorec pro hledání

Definice 1

Vektorový součin dvou vektorů je vektor kolmý na oba dané vektory a jeho délka bude rovna součinu délek těchto vektorů se sinem úhlu mezi těmito vektory a tento vektor se dvěma počátečními má stejnou orientaci jako kartézský souřadnicový systém.

Zápis: $\overline(α)х\overline(β)$.

Matematicky to vypadá takto:

1. $|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
3. $(\overline(α)х\overline(β),\overline(α),\overline(β))$ a $(\overline(i),\overline(j),\overline(k))$ jsou orientovány stejným způsobem (obr. 2)

Je zřejmé, že vnější součin vektorů se bude rovnat nulovému vektoru ve dvou případech:

1. Pokud je délka jednoho nebo obou vektorů nulová.
2. Pokud je úhel mezi těmito vektory roven $180^\circ$ nebo $0^\circ$ (protože v tomto případě je sinus roven nule).

Chcete-li jasně vidět, jak se nachází křížový součin vektorů, zvažte následující příklady řešení.

Příklad 1

Najděte délku vektoru $\overline(δ)$, který bude výsledkem křížového součinu vektorů, se souřadnicemi $\overline(α)=(0,4,0)$ a $\overline(β)=(3,0,0)$.

Řešení.

Znázorněme tyto vektory v kartézském souřadnicovém prostoru (obr. 3):

Obrázek 3. Vektory v kartézském souřadnicovém prostoru. Author24 - online výměna studentských prací

Vidíme, že tyto vektory leží na osách $Ox$ a $Oy$. Proto bude úhel mezi nimi roven $90^\circ$. Pojďme najít délky těchto vektorů:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

Pak podle definice 1 získáme modul $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

Odpověď: $ 12 $.

Výpočet křížového součinu podle souřadnic vektorů

Definice 1 okamžitě naznačuje způsob, jak najít křížový součin pro dva vektory. Protože vektor má kromě hodnoty také směr, je nemožné jej najít pouze pomocí skalární hodnoty. Ale kromě toho existuje další způsob, jak najít vektory, které nám byly přiděleny, pomocí souřadnic.

Dostaneme vektory $\overline(α)$ a $\overline(β)$, které budou mít souřadnice $(α_1,α_2,α_3)$ a $(β_1,β_2,β_3)$. Potom vektor křížového součinu (jmenovitě jeho souřadnice) lze najít podle následujícího vzorce:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

Jinak rozšířením determinantu získáme následující souřadnice

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Příklad 2

Najděte vektor křížového součinu kolineárních vektorů $\overline(α)$ a $\overline(β)$ se souřadnicemi $(0,3,3)$ a $(-1,2,6)$.

Řešení.

Použijme vzorec výše. Dostat

$\overline(α)x\overline(β)=\begin(vmatrix)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18-6)\overline(i)-(0+3)\overline(j)+(0+3)\2j)+(0+3)\2j)overline\overline\=1=\ (12,-3,3) $

Odpověď: $(12,-3,3)$.

Vlastnosti křížového součinu vektorů

Pro libovolné smíšené tři vektory $\overline(α)$, $\overline(β)$ a $\overline(γ)$ a také $r∈R$ platí následující vlastnosti:

Příklad 3

Najděte oblast rovnoběžníku, jehož vrcholy mají souřadnice $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ a $(3,8,0)$.

Řešení.

Nejprve nakreslete tento rovnoběžník v souřadnicovém prostoru (obr. 5):

Obrázek 5. Rovnoběžník v souřadnicovém prostoru. Author24 - online výměna studentských prací

Vidíme, že dvě strany tohoto rovnoběžníku jsou konstruovány pomocí kolineárních vektorů se souřadnicemi $\overline(α)=(3,0,0)$ a $\overline(β)=(0,8,0)$. Pomocí čtvrté vlastnosti získáme:

$S=|\overline(α)x\overline(β)|$

Najděte vektor $\overline(α)х\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline(i)-0\overline(j)+24\overline(k)=)$0,2

Proto

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

Než uvedeme pojem vektorového součinu, přejděme k otázce orientace uspořádané trojice vektorů a → , b → , c → v trojrozměrném prostoru.

Pro začátek dejme stranou vektory a → , b → , c → z jednoho bodu. Orientace trojice a → , b → , c → je pravá nebo levá v závislosti na směru vektoru c → . Ze směru, ve kterém je proveden nejkratší obrat z vektoru a → do b → od konce vektoru c → , bude určen tvar trojice a → , b → , c →.

Pokud je nejkratší rotace proti směru hodinových ručiček, nazývá se trojice vektorů a → , b → , c → že jo pokud ve směru hodinových ručiček - vlevo, odjet.

Dále vezměte dva nekolineární vektory a → a b → . Odložme tedy vektory A B → = a → a A C → = b → z bodu A. Sestrojme vektor A D → = c → , který je současně kolmý k A B → i A C → . Při konstrukci vektoru A D → = c → tedy můžeme udělat dvě věci a dát mu buď jeden směr, nebo opačný (viz obrázek).

Uspořádaná trojice vektorů a → , b → , c → může být, jak jsme zjistili, pravá nebo levá v závislosti na směru vektoru.

Z výše uvedeného si můžeme představit definici vektorového součinu. Tato definice udáváno pro dva vektory definované v pravoúhlý systém souřadnice trojrozměrného prostoru.

Definice 1

Vektorový součin dvou vektorů a → a b → budeme nazývat takový vektor daný v pravoúhlém souřadnicovém systému trojrozměrného prostoru takový, že:

• pokud jsou vektory a → a b → kolineární, bude nula;
• bude kolmá na vektor a →​​ i vektor b → tzn. ∠ a → c → = ∠ b → c → = π 2 ;
• jeho délka je určena vzorcem: c → = a → b → sin ∠ a → , b → ;
• trojice vektorů a → , b → , c → má stejnou orientaci jako daný souřadnicový systém.

Křížový součin vektorů a → a b → má následující zápis: a → × b → .

Křížové souřadnice produktu

Vzhledem k tomu, že jakýkoli vektor má v souřadnicovém systému určité souřadnice, je možné zavést druhou definici vektorového součinu, která vám umožní zjistit jeho souřadnice z daných souřadnic vektorů.

Definice 2

V pravoúhlém souřadnicovém systému trojrozměrného prostoru vektorový součin dvou vektorů a → = (a x ; a y ; a z) a b → = (b x ; b y ; b z) se nazývá vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kde i → , j → , k → jsou souřadnicové vektory.

Vektorový součin lze znázornit jako determinant čtvercové matice třetího řádu, kde první řádek jsou vektory i → , j → , k → , druhý řádek obsahuje souřadnice vektoru a → a třetí řádek obsahuje souřadnice vektoru b → v daném pravoúhlém souřadnicovém systému tento determinant matice vypadá takto: c → = a z b x x b → a y = i →

Rozšířením tohoto determinantu o prvky prvního řádku získáme rovnost: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = z = = a b x b x b y k → = z = = a b - a → x b → z b z) j → + (a x b y - a y b x) k →

Křížové vlastnosti produktu

Je známo, že vektorový součin v souřadnicích je reprezentován jako determinant matice c → = a → × b → = i → j → k → a x a y a z b x b y b z , pak na zákl. maticové determinantní vlastnosti následující vlastnosti vektorového produktu:

1. antikomutativnost a → × b → = - b → × a → ;
2. distributivita a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → nebo a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. asociativita λ a → × b → = λ a → × b → nebo a → × (λ b →) = λ a → × b → , kde λ je libovolné reálné číslo.

Tyto vlastnosti nemají složité důkazy.

Můžeme například dokázat vlastnost antikomutativity vektorového součinu.

Důkaz antikomutativnosti

Podle definice a → × b → = i → j → k → a x a y a z b x b y b z a b → × a → = i → j → k → b x b y b z a x a y az . A pokud jsou dva řádky matice zaměněny, pak by se hodnota determinantu matice měla změnit na opačnou, tedy a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , což dokazuje součinnost antikomu

Vektorový produkt - příklady a řešení

Ve většině případů existují tři typy úkolů.

V úlohách prvního typu se obvykle uvádějí délky dvou vektorů a úhel mezi nimi, ale musíte najít délku křížového součinu. V tomto případě použijte následující vzorec c → = a → b → sin ∠ a → , b → .

Příklad 1

Najděte délku křížového součinu vektorů a → a b → je-li známo a → = 3 , b → = 5 , ∠ a → , b → = π 4 .

Řešení

Pomocí definice délky vektorového součinu vektorů a → a b → vyřešíme tento problém: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Odpovědět: 15 2 2 .

Úlohy druhého typu mají souvislost se souřadnicemi vektorů, obsahují vektorový součin, jeho délku atp. se hledají přes známé souřadnice daných vektorů a → = (a x ; a y ; a z) A b → = (b x ; b y ; b z) .

U tohoto typu úloh můžete vyřešit spoustu možností úloh. Například ne souřadnice vektorů a → a b → , ale jejich expanze v souřadnicových vektorech tvaru b → = b x i → + b y j → + b z k → a c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , nebo vektory a → a b → mohou být dány souřadnicemi jejich počátečního a koncového bodu.

Zvažte následující příklady.

Příklad 2

V pravoúhlém souřadnicovém systému jsou zasazeny dva vektory a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Najděte jejich vektorový produkt.

Řešení

Druhou definicí najdeme vektorový součin dvou vektorů v daných souřadnicích: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i) → 1 - 2 (- 1) i) + 1 - 2 (- 3) ) k → = = - 2 i → - 2 j → - 2 k → .

Pokud vektorový součin zapíšeme přes maticový determinant, pak řešení tohoto příkladu je následující: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Odpovědět: a → × b → = - 2 i → - 2 j → - 2 k → .

Příklad 3

Najděte délku křížového součinu vektorů i → - j → a i → + j → + k → , kde i → , j → , k → - orty pravoúhlého kartézského souřadnicového systému.

Řešení

Nejprve najdeme souřadnice daného vektorového součinu i → - j → × i → + j → + k → v daném pravoúhlém souřadném systému.

Je známo, že vektory i → - j → a i → + j → + k → mají souřadnice (1 ; - 1 ; 0) a (1 ; 1; 1). Zjistíme délku vektorového součinu pomocí maticového determinantu, pak máme i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Proto vektorový součin i → - j → × i → + j → + k → má souřadnice (- 1 ; - 1 ; 2) v daný systém souřadnice.

Délku vektorového součinu zjistíme podle vzorce (viz část o zjištění délky vektoru): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Odpovědět: i → - j → × i → + j → + k → = 6 . .

Příklad 4

Souřadnice tří bodů A (1, 0, 1), B (0, 2, 3) ​​, C (1, 4, 2) jsou uvedeny v pravoúhlém kartézském souřadnicovém systému. Najděte nějaký vektor kolmý k A B → a A C → současně.

Řešení

Vektory A B → a AC → mají následující souřadnice (-1; 2; 2) a (0; 4; 1). Když jsme našli vektorový součin vektorů A B → a A C → , je zřejmé, že se jedná o kolmý vektor podle definice k A B → i A C → , to znamená, že je řešením našeho problému. Najděte to A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Odpovědět: - 6 i → + j → - 4 k → . je jedním z kolmých vektorů.

Problémy třetího typu jsou zaměřeny na využití vlastností vektorového součinu vektorů. Po jeho aplikaci získáme řešení daného problému.

Příklad 5

Vektory a → a b → jsou kolmé a jejich délky jsou 3 a 4. Najděte délku křížového součinu 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Řešení

Distribuční vlastností křížového součinu můžeme napsat 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Vlastností asociativnosti odebereme číselné koeficienty ze znaménka vektorových součinů v posledním výrazu: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) a → × b → + (- 1) a → × b → + (- 1) a → × b → + (- 1) (- 1) b- → 2 b – 2 b = - 6 a → × b → - b → × a → + 2 b → × b →

Vektorové součiny a → × a → a b → × b → se rovnají 0, protože a → × a → = a → a → sin 0 = 0 a b → × b → = b → b → sin 0 = 0, pak 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 b → → → b. .

Z antikomutativnosti vektorového součinu vyplývá - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Pomocí vlastností vektorového součinu získáme rovnost 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Podle podmínky jsou vektory a → a b → kolmé, to znamená, že úhel mezi nimi je roven π 2 . Nyní zbývá pouze dosadit nalezené hodnoty do příslušných vzorců: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a → , b →) = 5 3 4 sin π 2 = 60.

Odpovědět: 3 a → - b → × a → - 2 b → = 60 .

Délka křížového součinu vektorů podle definice je a → × b → = a → · b → · sin ∠ a → , b → . Protože je již známo (od školní kurz), že plocha trojúhelníku je polovinou součinu délek jeho dvou stran vynásobených sinem úhlu mezi danými stranami. Délka vektorového součinu se proto rovná ploše rovnoběžníku - zdvojeného trojúhelníku, jmenovitě součinu stran ve formě vektorů a → a b → , vysazených z jednoho bodu, sinusem úhlu mezi nimi sin ∠ a → , b → .

Toto je geometrický význam vektorového součinu.

Fyzikální význam vektorového součinu

V mechanice, jednom z odvětví fyziky, můžete díky vektorovému součinu určit moment síly vzhledem k bodu v prostoru.

Definice 3

Pod momentem síly F → , působícím na bod B , vzhledem k bodu A budeme chápat následující vektorový součin A B → × F → .

Pokud si všimnete chyby v textu, zvýrazněte ji a stiskněte Ctrl+Enter

V této lekci se podíváme na další dvě operace s vektory: křížový součin vektorů A smíšený součin vektorů (okamžitý odkaz pro ty, kteří to potřebují). Nevadí, občas se stane, že pro úplné štěstí navíc bodový součin vektorů, je potřeba víc a víc. Taková je závislost na vektoru. Člověk může mít dojem, že se dostáváme do džungle analytické geometrie. To je špatně. V této sekci vyšší matematiky je obecně málo palivového dříví, snad až na Pinocchio. Ve skutečnosti je materiál velmi běžný a jednoduchý - sotva obtížnější než stejný skalární součin, dokonce bude méně typických úkolů. Hlavní věcí v analytické geometrii, jak mnozí uvidí nebo již viděli, je NESMÝT VÝPOČTY. Opakujte jako kouzlo a budete šťastní =)

Pokud vektory jiskří někde daleko, jako blesky na obzoru, nevadí, začněte lekcí Vektory pro figuríny obnovit nebo znovu získat základní znalosti o vektorech. Připravenější čtenáři se mohou s informacemi seznámit selektivně, snažil jsem se shromáždit nejúplnější sbírku příkladů, které se často vyskytují praktická práce

Co vám udělá radost? Když jsem byl malý, uměl jsem žonglovat se dvěma a dokonce se třemi míčky. Dopadlo to dobře. Nyní není třeba vůbec žonglovat, protože to zvážíme pouze prostorové vektory a ploché vektory se dvěma souřadnicemi budou vynechány. Proč? Tak se zrodily tyto akce – vektor a smíšený součin vektorů jsou definovány a fungují v trojrozměrném prostoru. Už jednodušší!

V této operaci, stejným způsobem jako u skalárního součinu, dva vektory. Ať jsou to nehynoucí písmena.

Samotná akce označené následujícím způsobem: . Jsou i jiné možnosti, ale já jsem zvyklý křížový součin vektorů označovat takto, v hranatých závorkách křížkem.

A hned otázka: pokud v bodový součin vektorů jsou zapojeny dva vektory a zde jsou tedy dva vektory také násobeny jaký je rozdíl? Jasný rozdíl především ve VÝSLEDKU:

Výsledkem skalárního součinu vektorů je ČÍSLO:

Výsledkem křížového součinu vektorů je VEKTOR: , tedy vektory vynásobíme a dostaneme opět vektor. Uzavřený klub. Vlastně odtud název operace. V různé naučné literatuře se mohou označení také lišit, já použiji písmeno .

Definice křížového produktu

Nejprve bude definice s obrázkem, poté komentáře.

Definice: křížový produkt nekolineární vektory, v tomto pořadí, se nazývá VEKTOR, délka což je číselně rovná ploše rovnoběžníku, postavený na těchto vektorech; vektor ortogonální k vektorům a je nasměrován tak, aby základ měl správnou orientaci:

Rozebíráme definici podle kostí, je tam spousta zajímavých věcí!

Můžeme tedy zdůraznit následující důležité body:

1) Zdrojové vektory označené červenými šipkami podle definice ne kolineární. Případ kolineárních vektorů bude vhodné zvážit o něco později.

2) Pořízené vektory v přísném pořadí: – "a" se násobí "být", nikoli „být“ na „a“. Výsledek vektorového násobení je VECTOR , který je označen modře. Pokud jsou vektory vynásobeny v opačném pořadí, dostaneme vektor stejně dlouhý a opačný ve směru (karmínová barva). Tedy rovnost .

3) Nyní se seznámíme s geometrickým významem vektorového součinu. Toto je velmi důležitý bod! DÉLKA modrého vektoru (a tedy karmínového vektoru ) je číselně rovna OBLASTI rovnoběžníku postaveného na vektorech . Na obrázku je tento rovnoběžník vystínován černě.

Poznámka : výkres je schematický a jmenovitá délka křížového produktu se samozřejmě nerovná ploše rovnoběžníku.

Vzpomínáme na jeden z geometrické vzorce: plocha rovnoběžníku se rovná součinu sousedních stran a sinu úhlu mezi nimi. Na základě výše uvedeného tedy platí vzorec pro výpočet DÉLKY vektorového součinu:

Zdůrazňuji, že ve vzorci mluvíme o DÉLCE vektoru, nikoli o vektoru samotném. Jaký je praktický význam? A význam je takový, že v problémech analytické geometrie se oblast rovnoběžníku často nachází prostřednictvím konceptu vektorového produktu:

Dejme si vteřinku důležitý vzorec. Úhlopříčka rovnoběžníku (červená tečkovaná čára) jej rozděluje na dvě části rovný trojúhelník. Proto lze oblast trojúhelníku postaveného na vektorech (červené stínování) nalézt podle vzorce:

4) Neméně důležitým faktem je, že vektor je ortogonální k vektorům, tzn . Opačný vektor (karmínová šipka) je samozřejmě také ortogonální k původním vektorům.

5) Vektor směřuje tak, že základ Má to že jo orientace. V lekci o přechod na nový základ Mluvil jsem podrobně o rovinná orientace a nyní zjistíme, jaká je orientace prostoru. Vysvětlím na vašich prstech pravá ruka. Duševně kombinovat ukazováček s vektorem a prostředníček s vektorem. Prsteníček a malíček zatlačte do dlaně. Jako výsledek palec- vektorový součin vyhledá. Toto je správně orientovaný základ (je na obrázku). Nyní vyměňte vektory ( ukazováček a prostředníček) na některých místech se v důsledku toho palec otočí a vektorový součin se již bude dívat dolů. To je také správně orientovaný základ. Možná máte otázku: jaký základ má levá orientace? "Přiřadit" stejné prsty levá ruka vectors a získáte levou základnu a levou prostorovou orientaci (v tomto případě bude palec umístěn ve směru spodního vektoru). Obrazně řečeno, tyto základny „kroutí“ nebo orientují prostor v různých směrech. A tento koncept by neměl být považován za něco přitaženého nebo abstraktního - například nejobyčejnější zrcadlo mění orientaci prostoru, a pokud „vytáhnete odražený předmět ze zrcadla“, pak jej obecně nebude možné kombinovat s „originálem“. Mimochodem, přineste tři prsty k zrcadlu a analyzujte odraz ;-)

... jak je dobré, že o tom nyní víte orientované vpravo a vlevo základy, protože výroky některých přednášejících o změně orientace jsou hrozné =)

Vektorový součin kolineárních vektorů

Definice byla do detailu propracována, zbývá zjistit, co se stane, když jsou vektory kolineární. Pokud jsou vektory kolineární, pak je lze umístit na jednu přímku a náš rovnoběžník se také „složí“ do jedné přímky. Oblast takových, jak říkají matematici, degenerovat rovnoběžník je nulový. Totéž vyplývá ze vzorce - sinus nuly nebo 180 stupňů je roven nule, což znamená, že plocha je nulová

Tedy pokud , tak A . Vezměte prosím na vědomí, že samotný křížový součin se rovná nulovému vektoru, ale v praxi se to často zanedbává a píše se, že je také roven nule.

Speciálním případem je vektorový součin vektoru a samotného:

Pomocí křížového součinu můžete zkontrolovat kolinearitu trojrozměrných vektorů a tento úkol mimo jiné budeme také analyzovat.

Pro řešení praktické příklady může být vyžadováno trigonometrická tabulka najít z něj hodnoty sinů.

No, založíme oheň:

Příklad 1

a) Najděte délku vektorového součinu vektorů if

b) Najděte oblast rovnoběžníku postaveného na vektorech if

Řešení: Ne, nejedná se o překlep, záměrně jsem udělal výchozí údaje v položkách podmínky stejné. Protože design řešení bude jiný!

a) Podle podmínky je požadováno najít délka vektor (vektorový součin). Podle odpovídajícího vzorce:

Odpovědět:

Protože byl dotazován na délku, pak v odpovědi uvádíme rozměr - jednotky.

b) Podle stavu je požadováno najít náměstí paralelogram postavený na vektorech. Plocha tohoto rovnoběžníku se číselně rovná délce křížového produktu:

Odpovědět:

Upozorňuji, že v odpovědi o vektorovém součinu se vůbec nemluví, byli jsme dotázáni oblast postavy, respektive rozměr je čtvercových jednotek.

Vždy se podíváme na to, CO má podmínka najít, a na základě toho formulujeme Průhledná Odpovědět. Může se to zdát jako doslovnost, ale mezi učiteli je dost doslovníků a úkol s velkou šancí se vrátí k přepracování. I když se nejedná o nijak zvlášť napjatou hnidopišskou otázku – pokud je odpověď nesprávná, má člověk dojem, že daný člověk nerozumí jednoduchým věcem a/nebo nepochopil podstatu úkolu. Tento okamžik by měl být vždy pod kontrolou, řešit jakýkoli problém ve vyšší matematice i v jiných předmětech.

Kam zmizelo velké písmeno „en“? V zásadě by se to dalo dodatečně přilepit k řešení, ale v zájmu zkrácení záznamu jsem to neudělal. Doufám, že to všichni pochopí a je to označení to samé.

Populární příklad pro nezávislé řešení:

Příklad 2

Najděte oblast trojúhelníku postaveného na vektorech if

Vzorec pro nalezení oblasti trojúhelníku pomocí vektorového produktu je uveden v komentářích k definici. Řešení a odpověď na konci lekce.

V praxi je úkol opravdu velmi běžný, trojúhelníky lze obecně mučit.

K vyřešení dalších problémů potřebujeme:

Vlastnosti křížového součinu vektorů

Některé vlastnosti vektorového součinu jsme již zvažovali, nicméně do tohoto seznamu je zařadím.

Pro libovolné vektory a libovolné číslo platí následující vlastnosti:

1) V jiných zdrojích informací se tato položka obvykle ve vlastnostech nerozlišuje, ale z praktického hlediska je velmi důležitá. Tak to nech být.

2) - vlastnost je také probírána výše, někdy je tzv antikomutativnost. Jinými slovy, na pořadí vektorů záleží.

3) - kombinace popř asociativní zákony vektorového produktu. Konstanty lze snadno vyjmout z limitů vektorového součinu. Vážně, co tam dělají?

4) - distribuce popř rozdělení zákony vektorového produktu. Problémy nejsou ani s otevíráním závorek.

Jako demonstraci uvažujme krátký příklad:

Příklad 3

Najdi jestli

Řešení: Podle podmínky je opět nutné najít délku vektorového součinu. Namalujeme naši miniaturu:

(1) Podle asociativních zákonů vyjmeme konstanty za hranice vektorového součinu.

(2) Vyjmeme konstantu z modulu, zatímco modul „sežere“ znaménko mínus. Délka nemůže být záporná.

(3) Co následuje, je jasné.

Odpovědět:

Je čas hodit dřevo do ohně:

Příklad 4

Vypočítejte obsah trojúhelníku postaveného na vektorech, jestliže

Řešení: Najděte obsah trojúhelníku pomocí vzorce . Zádrhel je v tom, že vektory "ce" a "te" jsou samy reprezentovány jako součty vektorů. Algoritmus je zde standardní a trochu připomíná příklady č. 3 a 4 z lekce. Bodový součin vektorů. Pro přehlednost si to rozdělíme do tří kroků:

1) V prvním kroku vyjádříme vektorový produkt prostřednictvím vektorového produktu, ve skutečnosti, vyjádřit vektor pomocí vektoru. O délce zatím nepadlo slovo!

(1) Dosazujeme výrazy vektorů .

(2) Pomocí distributivních zákonů otevřete závorky podle pravidla násobení polynomů.

(3) Pomocí asociativních zákonů vyjmeme všechny konstanty za vektorovými součiny. S malými zkušenostmi lze akce 2 a 3 provádět současně.

(4) První a poslední člen jsou rovny nule (nulový vektor) kvůli příjemné vlastnosti . Ve druhém členu používáme vlastnost antikomutativity vektorového součinu:

(5) Uvádíme podobné termíny.

V důsledku toho se ukázalo, že vektor je vyjádřen prostřednictvím vektoru, což bylo to, co bylo požadováno, aby bylo dosaženo:

2) Ve druhém kroku najdeme délku vektorového součinu, kterou potřebujeme. Tato akce je podobná příkladu 3:

3) Najděte oblast požadovaného trojúhelníku:

Kroky 2-3 řešení by mohly být uspořádány v jedné řadě.

Odpovědět:

Uvažovaný problém je poměrně častý v kontrolní práce, zde je příklad řešení pro kutily:

Příklad 5

Najdi jestli

Krátké řešení a odpověď na konci lekce. Podívejme se, jak pozorní jste byli při studiu předchozích příkladů ;-)

Křížový součin vektorů v souřadnicích

, uvedené na ortonormálním základě , se vyjadřuje vzorcem:

Vzorec je opravdu jednoduchý: vektory souřadnic zapíšeme do horního řádku determinantu, souřadnice vektorů „zabalíme“ do druhého a třetího řádku a vložíme v přísném pořadí- nejprve souřadnice vektoru "ve", potom souřadnice vektoru "double-ve". Pokud je třeba vektory násobit v jiném pořadí, měly by být řádky také prohozeny:

Příklad 10

Zkontrolujte, zda jsou následující prostorové vektory kolineární:
A)
b)

Řešení: Test je založen na jednom z tvrzení v této lekci: pokud jsou vektory kolineární, pak je jejich křížový součin nula (nulový vektor): .

a) Najděte vektorový součin:

Takže vektory nejsou kolineární.

b) Najděte vektorový součin:

Odpovědět: a) není kolineární, b)

Zde jsou snad všechny základní informace o vektorovém součinu vektorů.

Tato část nebude příliš rozsáhlá, protože existuje jen málo problémů, kde se používá smíšený součin vektorů. Ve skutečnosti bude vše spočívat na definici, geometrickém významu a několika pracovních vzorcích.

smíšený produkt vektory je součin tří vektorů:

Takto se seřadili jako vlak a čekají, nemohou se dočkat, až budou spočítáni.

Nejprve opět definice a obrázek:

Definice: Smíšený produkt nekoplanární vektory, v tomto pořadí, je nazýván objem rovnoběžnostěnu, postavený na těchto vektorech, vybavený znaménkem „+“, pokud je základ pravý, a znaménkem „-“, pokud je základ vlevo.

Pojďme udělat kresbu. Pro nás neviditelné čáry jsou nakresleny tečkovanou čarou:

Pojďme se ponořit do definice:

2) Pořízené vektory v určitém pořadí, tedy permutace vektorů v součinu, jak asi tušíte, nezůstane bez následků.

3) Než se vyjádřím ke geometrickému významu, poznamenám zřejmý fakt: smíšeným součinem vektorů je ČÍSLO: . V naučné literatuře může být design poněkud odlišný, používám k označení smíšeného produktu skrz a výsledek výpočtů písmenem "pe".

A-převorství smíšený produkt je objem rovnoběžnostěnu, postavené na vektorech (postava je nakreslena červenými vektory a černými čarami). To znamená, že číslo se rovná objemu daného rovnoběžnostěnu.

Poznámka : Výkres je schematický.

4) Netrapme se opět pojmem orientace základny a prostoru. Smyslem závěrečné části je, že k objemu lze přidat znaménko mínus. Jednoduše řečeno, smíšený produkt může být záporný: .

Vzorec pro výpočet objemu rovnoběžnostěnu postaveného na vektorech vyplývá přímo z definice.