VEKTORIDE ristprodukti kasutamine

pindala arvutamiseks

mõned geomeetrilised kujundid

Uurimine matemaatika

Õpilane 10 B klass

MOU keskkool nr 73

Perevoznikov Mihhail

Juhid:

Matemaatikaõpetaja MOU keskkooli nr 73 Dragunova Svetlana Nikolaevna

Osakonna assistent. matemaatiline analüüs SSU mehaanika-matemaatikateaduskond N.G. Tšernõševski Berdnikov Gleb Sergejevitš

Saratov, 2015

Sissejuhatus.

1. Teoreetiline ülevaade.

1.1. Vektorid ja arvutused vektoritega.

1.2. Vektorite skalaarkorrutise kasutamine ülesannete lahendamisel

1.3 Vektorite punktkorrutis koordinaatides

1.4. Vektorite vektorkorrutis kolmemõõtmelises eukleidilises ruumis: mõiste määratlus.

1.5. Vektori koordinaadid vektorite korrutised.

2. Praktiline osa.

2.1. Ristkorrutise seos kolmnurga ja rööpküliku pindalaga. Vektorite vektorkorrutise valemi ja geomeetrilise tähenduse tuletamine.

2.2. Teades ainult punktide koordinaate, leidke kolmnurga pindala. Teoreemi tõestus

2.3. Valemi õigsuse kontrollimine näidete põhjal.

2.4. Vektoralgebra praktiline kasutamine ja vektorite korrutis.

Järeldus

Sissejuhatus

Nagu teate, on paljudel geomeetrilistel ülesannetel kaks peamist lahendust – graafiline ja analüütiline. Graafilist meetodit seostatakse graafikute ja jooniste konstrueerimisega ning analüütiline meetod hõlmab probleemide lahendamist peamiselt algebralised tehted. Viimasel juhul on ülesannete lahendamise algoritm seotud analüütilise geomeetriaga. Analüütiline geomeetria on matemaatika haru, õigemini lineaaralgebra, mis käsitleb geomeetriliste ülesannete lahendamist algebra abil, lähtudes koordinaatide meetodil tasapinnal ja ruumis. Analüütiline geomeetria võimaldab analüüsida geomeetrilisi kujutisi, uurida jooni ja pindu, mis on praktiliste rakenduste jaoks olulised. Veelgi enam, selles teaduses kasutatakse kujundite ruumilise mõistmise laiendamiseks mõnikord ka vektorite vektorkorrutist.

Kolmemõõtmeliste ruumitehnoloogiate laialdase kasutuse tõttu tundub mõne geomeetrilise kujundi omaduste uurimine vektorkorrutise abil asjakohane.

Sellega seoses tehti kindlaks selle projekti eesmärk - vektorite ristkorrutise kasutamine mõne geomeetrilise kujundi pindala arvutamiseks.

Selle eesmärgiga seoses lahendati järgmised ülesanded:

1. Teoreetiliselt uurida vektoralgebra vajalikke aluseid ja määratleda vektorite vektorkorrutis koordinaatsüsteemis;

2. Analüüsige seose olemasolu vektorkorrutise ning kolmnurga ja rööpküliku pindala vahel;

3. Tuletage kolmnurga ja rööpküliku pindala valem koordinaatides;

4. Kontrollige konkreetseid näiteid tuletatud valemi õigsus.

1. Teoreetiline ülevaade.

1. Vektorid ja arvutused vektoritega

Vektor on suunatud segment, millele on märgitud selle algus ja lõpp:

Sel juhul on punktiks segmendi algus A, on lõigu lõpp punkt IN. Vektorit ennast tähistatakse
või . Vektori koordinaatide leidmiseks
, teades selle alguspunktide A ja lõpp-punkti B koordinaate, on vaja lõpp-punkti koordinaatidest lahutada vastavad alguspunkti koordinaadid:

= { B x - A x ; B y - A y }

Vektoreid, mis asuvad paralleelsetel või samal sirgel, nimetatakse kollineaarseks. Sel juhul on vektor segment, mida iseloomustavad pikkus ja suund.

Suunatud segmendi pikkus määrab vektori arvväärtuse ja seda nimetatakse vektori pikkuseks või vektori mooduliks.

Vektori pikkus || ristkülikukujuliselt Descartes'i koordinaadid on võrdne ruutjuur selle koordinaatide ruutude summast.

Vektoritega saab hakkama erinevaid tegevusi.

Näiteks lisamine. Nende lisamiseks peate esmalt joonistama teise vektori esimese lõpust ja seejärel ühendama esimese vektori teise lõpuga (joonis 1). Vektorite summa on veel üks vektor uute koordinaatidega.

Vektorite summa = {a x ; a y) Ja = {b x ; b y) leiate järgmise valemi abil:

+ = (a x +b x ; a y +b y }

Riis. 1. Tegevused vektoritega

Vektorite lahutamisel tuleb need kõigepealt ühest punktist joonistada ja seejärel ühendada teise ots esimese otsaga.

Vektori erinevus = {a x ; a y) Ja = {b x ; b y } võib leida järgmise valemi abil:

- = { a x -b x ; a y -b y }

Samuti saab vektoreid korrutada arvuga. Tulemuseks on ka vektor, mis on antud vektorist k korda suurem (või väiksem). Selle suund sõltub k märgist: kui k on positiivne, on vektorid samas suunas ja kui k on negatiivne, on nad vastupidise suunaga.

Vektortoode = {a x ; a y } ja arvu k saab leida järgmise valemi abil:

k = (k a x ; k a y }

Kas vektorit on võimalik vektoriga korrutada? Muidugi ja isegi kaks võimalust!

Esimene võimalus on skalaarkorrutis.

Riis. 2. Punktkorrutis koordinaatides

Vektorite korrutise leidmiseks võite kasutada nende vektorite vahelist nurka , mis on näidatud joonisel 3.

Valemist järeldub, et skalaarkorrutis on võrdne nende vektorite pikkuste ja nendevahelise nurga koosinuse korrutisega, selle tulemuseks on arv. On oluline, et kui vektorid on risti, siis nende skalaarkorrutis on võrdne nulliga, sest koosinus täisnurk nende vahel on null.

IN koordinaattasand vektoril on ka koordinaadid. IN vektorid, nende koordinaadid ja punktkorrutis on ühed kõige mugavamad meetodid sirgete (või nende lõikude) vahelise nurga arvutamiseks, kui sisestatakse koordinaatsüsteem.Ja kui koordinaadid
, siis on nende skalaarkorrutis:

Kolmemõõtmelises ruumis on 3 telge ja vastavalt sellele on sellise süsteemi punktidel ja vektoritel igaühel 3 koordinaati ning vektorite skalaarkorrutis arvutatakse valemiga:

1.2. Kolmemõõtmelise ruumi vektorite vektorkorrutis.

Teine võimalus vektorite korrutise arvutamiseks on vektorkorrutis. Kuid selle määramiseks pole vaja enam tasapinda, vaid kolmemõõtmelist ruumi, milles vektori alguses ja lõpus on kumbki 3 koordinaati.

Erinevalt vektorite skalaarkorrutisest kolmemõõtmelises ruumis annab vektorite "vektori korrutamise" operatsioon teistsuguse tulemuse. Kui eelmisel kahe vektori skalaarkorrutise puhul oli tulemuseks arv, siis vektorite vektorkorrutise korral on tulemuseks teine ​​vektor, mis on risti mõlema korrutisesse sisenenud vektoriga. Seetõttu nimetatakse seda vektorite korrutist vektorkorrutiseks.

Ilmselgelt saadud vektori konstrueerimisel , risti kahe tootesse sisestanud suunaga - ja , saab valida kaks vastassuunda. Sel juhul saadud vektori suund määratakse parema käe reegli ehk gimleti reegliga. Kui joonistada vektorid nii, et nende algus langeb kokku ja pöörata esimene kordaja vektor lühimat teed pidi teise kordaja vektori suunas ning parema käe neli sõrme näitavad pöörlemissuunda (nagu kataks pöörlevat silindrit), siis näitab väljaulatuv pöial korrutisvektori suunda (joonis 7).

Riis. 7. Parema käe reegel

1.3. Vektorite ristkorrutise omadused.

Saadud vektori pikkus määratakse valemiga

.

Kus
vektorprodukt. Nagu eespool mainitud, on saadud vektor risti
, ja selle suuna määrab parema käe reegel.

Vektorkorrutis sõltub tegurite järjestusest, nimelt:

Nullist erineva vektorite ristkorrutis on 0, kui need on kollineaarsed, siis on nendevahelise nurga siinus 0.

Vektorite koordinaate kolmemõõtmelises ruumis väljendatakse järgmiselt: . Seejärel leitakse valemi abil saadud vektori koordinaadid

Saadud vektori pikkus leitakse valemiga:

.

2. Praktiline osa.

2.1. Vektorkorrutise ühendus kolmnurga ja rööpküliku pindalaga tasapinnal. Vektorite ristkorrutise geomeetriline tähendus.

Olgu meile antud kolmnurk ABC (joonis 8). On teada, et.

Kui kujutame kolmnurga AB ja AC külgi kahe vektorina, siis kolmnurga pindala valemist leiame vektorite ristkorrutise avaldise:

Ülaltoodust saame määrata vektorkorrutise geomeetrilise tähenduse (joonis 9):

vektorite ristkorrutise pikkus on võrdne vektorite külgedega kolmnurga kahekordse pindalaga ja , kui need on ühest punktist kõrvale jäetud.

Teisisõnu, vektorite ja ristkorrutise pikkus on võrdne rööpküliku pindala, ehitatud vektoritele ja , mille küljed ja ja nendevaheline nurk on võrdne .

Riis. 9. Vektorite vektorkorrutise geomeetriline tähendus

Sellega seoses saame anda vektorite vektorkorrutisele veel ühe definitsiooni :

Vektori ristkorrutis vektoril nimetatakse vektoriks , mille pikkus on arvuliselt võrdne vektoritele ehitatud rööpküliku pindalaga ja , risti nende vektorite tasapinnaga ja suunatud nii, et vähim pöörlemine alates k vektori ümber viidi läbi vastupäeva vektori otsast vaadatuna (joonis 10).

Riis. 10. Vektorite ristkorrutise definitsioon

rööpküliku abil

2.2. Valemi tuletamine kolmnurga pindala leidmiseks koordinaatides.

Niisiis, meile antakse tasapinnas kolmnurk ABC ja selle tippude koordinaadid. Leiame selle kolmnurga pindala (joonis 11).

Riis. 11. Näide kolmnurga pindala leidmise ülesande lahendamisest selle tippude koordinaatide järgi

Lahendus.

Kõigepealt arvestage tippude koordinaadid ruumis ja arvutage vektorite AB ja AC koordinaadid.

Vastavalt ülaltoodud valemile arvutame nende vektorkorrutise koordinaadid. Selle vektori pikkus võrdub kolmnurga ABC 2 alaga. Kolmnurga pindala on 10.

Veelgi enam, kui vaadelda kolmnurka tasapinnal, on vektorkorrutise kaks esimest koordinaati alati null, nii et saame sõnastada järgmise teoreemi.

Teoreem: Olgu antud kolmnurk ABC ja selle tippude koordinaadid (joonis 12).

Siis .

Riis. 12. Teoreemi tõestus

Tõestus.

Vaatleme ruumi punkte ja arvutame vektorite BC ja BA koordinaadid. . Kasutades ülaltoodud valemit, arvutame nende vektorite ristkorrutise koordinaadid. Pange tähele, et kõik terminid sisaldavadz 1 või z 2 on võrdne 0-ga, sest z 1i z 2 = 0. EEMALDA!!!

Seega, seega

2.3. Valemi õigsuse kontrollimine näidete pealt

Leidke vektorite moodustatud kolmnurga pindala a = (-1; 2; -2) ja b = (2; 1; -1).

Lahendus: Leiame nende vektorite ristkorrutise:

a ×b=

I(2 (-1) - (-2) 1) - j((-1) (-1) - (-2) 2) + k((-1) 1 - 2 2) =

I(-2 + 2) - j(1 + 4) + k(-1 - 4) = -5 j - 5 k = (0; -5; -5)

Vektorkorrutise omadustest:

SΔ =

| a×b| =

√ 02 + 52 + 52 =

√ 25 + 25 =

√ 50 =

5√ 2

Vastus: SΔ = 2,5√2.

Järeldus

2.4. Vektoralgebra rakendused

ning vektorite skalaar- ja ristkorrutis.

Kus on vektoreid vaja? Vektorruum ja vektorid pole mitte ainult teoreetilised, vaid neil on ka väga reaalsed praktilised rakendused kaasaegne maailm.

Mehaanikas ja füüsikas on paljudel suurustel mitte ainult arvväärtus, vaid ka suund. Selliseid suurusi nimetatakse vektorsuurusteks. Koos elementaarsete mehaaniliste mõistete kasutamisega, tuginedes neile füüsiline tähendus, loetakse paljusid suurusi libisevateks vektoriteks ja nende omadusi kirjeldatakse nii aksioomide abil, nagu teoreetilises mehaanikas tavaks, kui ka matemaatilised omadused vektorid. Kõige ilmekamad näited vektorkogused on kiirus, impulss ja jõud (joonis 12). Näiteks nurkimpulss ja Lorentzi jõud on vektorite abil matemaatiliselt kirjas.

Füüsikas pole olulised mitte ainult vektorid ise, vaid suurel määral on olulised ka nende korrutised, mis aitavad välja arvutada mõningaid suurusi. Ristkorrutis on kasulik vektorite kollineaarsuse määramiseks.Kahe vektori ristkorrutise moodul on võrdne nende moodulite korrutisega, kui need on risti, ja väheneb nullini, kui vektorid on kaas- või vastassuunalised.

Teise näitena kasutatakse punktkorrutist töö arvutamiseks alloleva valemi abil, kus F on jõuvektor ja s on nihkevektor.

Üks näide vektorite korrutise kasutamisest on jõumoment, mis võrdub pöörlemisteljelt jõu rakenduspunktini tõmmatud raadiusvektori korrutisega ja selle jõu vektori korrutisega.

Suur osa sellest, mida füüsikas arvutatakse parema käe reegli järgi, on ristkorrutis. Otsige tõendeid, tooge näiteid.

Märkimist väärib ka see, et vektorruumide võimalikud variandid ei piirdu ainult kahe- ja kolmemõõtmelise ruumiga. Kõrgem matemaatika arvestab suuremate mõõtmetega ruume, milles on määratletud ka skalaar- ja vektorkorrutise valemite analoogid. Hoolimata asjaolust, et ruumid, mille mõõtmed on suuremad kui 3, ei suuda inimmõistus visualiseerida, leiavad need üllatuslikult rakendusi paljudes teaduse ja tööstuse valdkondades.

Samas ei ole kolmemõõtmelises eukleidilises ruumis vektorite ristkorrutise tulemus mitte arv, vaid saadud vektor oma koordinaatide, suuna ja pikkusega.

Saadud vektori suuna määrab parema käe reegel, mis on analüütilise geomeetria üks üllatavamaid sätteid.

Vektorite ristkorrutist saab kasutada kolmnurga või rööpküliku pindala leidmisel tippude koordinaatidega, mis kinnitati valemi tuletamise, teoreemi tõestamise ja lahendamisega. praktilisi ülesandeid.

Vektoreid kasutatakse laialdaselt füüsikas, kus selliseid näitajaid nagu kiirus, impulss ja jõud saab esitada vektorsuurustena ja arvutada geomeetriliselt.

Kasutatud allikate loetelu

Atanasjan L. S., Butuzov V. F., Kadomtsev S. B. jt Geomeetria. 7.-9. klass: õpik haridusorganisatsioonidele. M.: , 2013. 383 lk.

Atanasjan L.S., Butuzov V.F., Kadomtsev S.B. jt Geomeetria. 10-11 klass: õpik haridusorganisatsioonidele: põhi- ja profiili tasemed. M.: , 2013. 255 lk.

Bugrov Ya.S., Nikolsky S.M. Kõrgem matemaatika. Esimene köide: Lineaaralgebra ja analüütilise geomeetria elemendid.

Kletenik D.V. Analüütilise geomeetria ülesannete kogu. Moskva: Nauka, Fizmatlit, 1998.

Analüütiline geomeetria.

Matemaatika. Ristik.

Matemaatika õppimine võrgus.

http://ru.onlinemschool.com/math/library/vector/multiply1/

V. Glaznevi koduleht.

http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm

Vikipeedia.

https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED %E8%E5

Ilmselgelt on ristkorrutise puhul oluline vektorite võtmise järjekord, pealegi

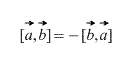
Samuti tuleneb definitsioonist otse, et mis tahes skalaarteguri k (arv) puhul kehtib järgmine:

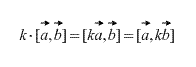
Kollineaarsete vektorite ristkorrutis on võrdne nullvektoriga. Pealegi on kahe vektori ristkorrutis null siis ja ainult siis, kui need on kollineaarsed. (Juhul kui üks neist on nullvektor, tuleb meeles pidada, et nullvektor on definitsiooni järgi mis tahes vektoriga kollineaarne).

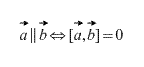
Vektortootel on jaotusvara, see on

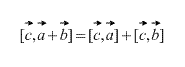
Ristkorrutise avaldis vektorite koordinaatidena.

Olgu antud kaks vektorit

(kuidas leida vektori koordinaate selle alguse ja lõpu koordinaatide järgi – vaata artiklit Vektorite punktkorrutis, lõik Punktkorrutise alternatiivne määratlus ehk kahe vektori punktkorrutise arvutamine nende koordinaatide järgi.)

Miks on vaja vektortoodet?

Ristkorrutise kasutamiseks on palju võimalusi, näiteks, nagu juba eespool kirjutatud, saab kahe vektori ristkorrutise arvutamisel teada, kas need on kollineaarsed.

Või saab seda kasutada nendest vektoritest koostatud rööpküliku pindala arvutamiseks. Definitsiooni põhjal on saadud vektori pikkus selle rööpküliku pindala.

Samuti on elektri ja magnetismi valdkonnas palju rakendusi.

Vektorprodukti veebikalkulaator.

Kahe vektori skalaarkorrutise leidmiseks selle kalkulaatori abil tuleb esimesele reale sisestada esimese vektori koordinaadid. teine ​​- teine. Vektorite koordinaate saab arvutada nende algus- ja lõppkoordinaatide järgi (vt artiklit Vektorite punktkorrutis , üksus Punktkorrutise alternatiivne määratlus või kahe vektori punktkorrutise arvutamine nende koordinaatide alusel.)

Nurk vektorite vahel

Kahe vektori ristkorrutise kontseptsiooni juurutamiseks peame esmalt käsitlema sellist mõistet nagu nurk nende vektorite vahel.

Olgu meile antud kaks vektorit $\overline(α)$ ja $\overline(β)$. Võtame ruumis mingi punkti $O$ ja jätame sellest kõrvale vektorid $\overline(α)=\overline(OA)$ ja $\overline(β)=\overline(OB)$, seejärel nurga $AOB $ nimetatakse nende vektorite vaheliseks nurgaks (joonis 1).

Tähistus: $∠(\overline(α),\overline(β))$

Vektorite ristkorrutise mõiste ja leidmise valem

Definitsioon 1

Kahe vektori vektorkorrutis on vektor, mis on risti mõlema antud vektoriga ja selle pikkus võrdub nende vektorite pikkuste korrutisega nende vektori vahelise nurga siinusega ja sellel vektoril, millel on kaks algset vektorit, on sama orientatsioon kui Descartes'i koordinaatsüsteem.

Tähistus: $\overline(α)х\overline(β)$.

Matemaatiliselt näeb see välja selline:

1. $|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
3. $(\overline(α)x\overline(β),\overline(α),\overline(β))$ ja $(\overline(i),\overline(j),\overline(k))$ on sama suunitlusega (joonis 2)

Ilmselt võrdub vektorite väliskorrutis nullvektoriga kahel juhul:

1. Kui ühe või mõlema vektori pikkus on null.
2. Kui nende vektorite vaheline nurk on võrdne $180^\circ$ või $0^\circ$ (sest sel juhul on siinus võrdne nulliga).

Et näha selgelt, kuidas vektorite ristkorrutis leitakse, vaadake järgmisi lahendusnäiteid.

Näide 1

Leidke vektori $\overline(δ)$ pikkus, mis on vektorite ristkorrutise tulemus koordinaatidega $\overline(α)=(0,4,0)$ ja $\overline(β) =(3,0,0 )$.

Lahendus.

Kujutame neid vektoreid Descartes'i koordinaatruumis (joonis 3):

Joonis 3. Vektorid ristkoordinaadiruumis. Autor24 - üliõpilastööde veebivahetus

Näeme, et need vektorid asuvad vastavalt $Ox$ ja $Oy$ telgedel. Seetõttu on nende vaheline nurk võrdne $90^\circ$. Leiame nende vektorite pikkused:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

Seejärel saame 1. definitsiooni järgi mooduli $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

Vastus: 12 dollarit.

Ristkorrutise arvutamine vektorite koordinaatide järgi

Definitsioon 1 viitab kohe võimalusele leida kahe vektori ristkorrutis. Kuna vektoril on lisaks väärtusele ka suund, siis pole seda võimalik ainult skalaarväärtust kasutades leida. Kuid peale selle on veel üks viis koordinaatide abil meile antud vektorite leidmiseks.

Olgu meile antud vektorid $\overline(α)$ ja $\overline(β)$, millel on vastavalt $(α_1,α_2,α_3)$ ja $(β_1,β_2,β_3)$ koordinaadid. Seejärel saab ristkorrutise vektori (nimelt selle koordinaadid) leida järgmise valemiga:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

Vastasel juhul saame determinanti laiendades järgmised koordinaadid

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3, α_1 β_2-α_2 β_1)$

Näide 2

Leia koordinaatidega $(0,3,3)$ ja $(-1,2,6)$ kollineaarsete vektorite $\overline(α)$ ja $\overline(β)$ ristkorrutise vektor.

Lahendus.

Kasutame ülaltoodud valemit. Hangi

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$

Vastus: $(12,-3,3)$.

Vektorite ristkorrutise omadused

Kolme suvalise segatud vektori $\overline(α)$, $\overline(β)$ ja $\overline(γ)$, samuti $r∈R$ puhul kehtivad järgmised omadused:

Näide 3

Leidke rööpküliku pindala, mille tippude koordinaadid on $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ ja $(3,8,0) $.

Lahendus.

Kõigepealt joonistage see rööpkülik koordinaatruumi (joonis 5):

Joonis 5. Parallelogramm koordinaatruumis. Autor24 - üliõpilastööde veebivahetus

Näeme, et selle rööpküliku kaks külge on konstrueeritud kasutades kollineaarseid vektoreid koordinaatidega $\overline(α)=(3,0,0)$ ja $\overline(β)=(0,8,0)$. Neljandat omadust kasutades saame:

$S=|\overline(α)x\overline(β)|$

Leidke vektor $\overline(α)х\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

Seega

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

Enne vektorkorrutise mõiste andmist pöördugem vektorite järjestatud kolmiku a → , b → , c → orientatsiooni kolmemõõtmelises ruumis.

Alustuseks paneme ühest punktist kõrvale vektorid a → , b → , c →. Kolmiku a → , b → , c → orientatsioon on olenevalt vektori c → suunast paremale või vasakule. Suuna järgi, kuhu vektorist a → b → vektori c → lõpust tehakse lühim pööre, määratakse kolmiku a → , b → , c → vorm.

Kui lühim pöörlemine on vastupäeva, siis vektorite kolmik a → , b → , c → nn. õige kui päripäeva - vasakule.

Järgmiseks võtame kaks mittekollineaarset vektorit a → ja b → . Lükkame siis vektorid A B → = a → ja A C → = b → punktist A edasi. Konstrueerime vektori A D → = c → , mis on samaaegselt risti nii A B → kui ka A C → . Seega saame vektori A D → = c → konstrueerimisel teha kahte asja, andes sellele kas ühe suuna või vastupidi (vt joonist).

Vektorite järjestatud kolmik a → , b → , c → võib, nagu saime teada, olenevalt vektori suunast olla parem- või vasakpoolne.

Ülaltoodust saame tutvustada vektorkorrutise definitsiooni. See määratlus antud kahe punktis määratletud vektori jaoks ristkülikukujuline süsteem kolmemõõtmelised ruumi koordinaadid.

Definitsioon 1

Kahe vektori a → ja b → vektorkorrutis me nimetame kolmemõõtmelise ruumi ristkülikukujulises koordinaatsüsteemis antud vektorit nii, et:

• kui vektorid a → ja b → on kollineaarsed, on see null;
• see on risti nii vektori a →​ kui ka vektori b → suhtes, st. ∠ a → c → = ∠ b → c → = π 2 ;
• selle pikkus määratakse valemiga: c → = a → b → sin ∠ a → , b → ;
• vektorite kolmik a → , b → , c → on sama orientatsiooniga kui antud koordinaatsüsteem.

Vektorite a → ja b → ristkorrutis on järgmise tähistusega: a → × b → .

Toote koordinaadid

Kuna igal vektoril on koordinaatide süsteemis teatud koordinaadid, on võimalik kasutusele võtta vektori korrutise teine ​​definitsioon, mis võimaldab leida vektorite antud koordinaatide järgi selle koordinaadid.

2. definitsioon

Kolmemõõtmelise ruumi ristkülikukujulises koordinaatsüsteemis kahe vektori a → = (a x ; a y ; a z) ja b → = (b x ; b y ; b z) vektorkorrutis nimetada vektorit c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kus i → , j → , k → on koordinaatvektorid.

Vektorkorrutist saab esitada kolmandat järku ruutmaatriksi determinandina, kus esimene rida on ortavektorid i → , j → , k → , teine ​​rida sisaldab vektori a → koordinaate ja kolmas rida. on vektori b → koordinaadid antud ristkülikukujulises koordinaatsüsteemis, maatriksdeterminant näeb välja selline: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Laiendades seda determinanti üle esimese rea elementide, saame võrdsuse: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a k → b = = × b y a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Risttoodete omadused

Teada on, et vektorkorrutis koordinaatides esitatakse maatriksi determinandina c → = a → × b → = i → j → k → a x a y a z b x b y b z , siis baasil maatriksi determinantide omadused järgnev vektori toote omadused:

1. antikommutatiivsus a → × b → = - b → × a → ;
2. jaotus a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → või a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. assotsiatiivsus λ a → × b → = λ a → × b → või a → × (λ b →) = λ a → × b → , kus λ on suvaline reaalarv.

Nendel omadustel pole keerulisi tõestusi.

Näiteks saame tõestada vektorkorrutise antikommutatiivsuse omadust.

Antikommutatiivsuse tõend

Definitsiooni järgi a → × b → = i → j → k → a x a y a z b x b y b z ja b → × a → = i → j → k → b x b y b z a x a y a z . Ja kui maatriksi kaks rida on vahetatud, siis peaks maatriksi determinandi väärtus muutuma vastupidiseks, seega a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , mis tõestab vektori korrutise antikommutatiivsust.

Vektortoode – näited ja lahendused

Enamasti on kolme tüüpi ülesandeid.

Esimest tüüpi ülesannetes on tavaliselt antud kahe vektori pikkused ja nendevaheline nurk, kuid tuleb leida ristkorrutise pikkus. Sel juhul kasutage järgmist valemit c → = a → b → sin ∠ a → , b → .

Näide 1

Leia vektorite a → ja b → ristkorrutise pikkus, kui on teada a → = 3 , b → = 5 , ∠ a → , b → = π 4.

Lahendus

Kasutades vektorite a → ja b → vektorkorrutise pikkuse definitsiooni, lahendame ülesande: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Vastus: 15 2 2 .

Teist tüüpi ülesannetel on seos vektorite koordinaatidega, need sisaldavad vektorkorrutist, selle pikkust jne. otsitakse antud vektorite teadaolevate koordinaatide kaudu a → = (a x ; a y ; a z) Ja b → = (b x ; b y ; b z) .

Seda tüüpi ülesannete puhul saate lahendada palju ülesannete valikuid. Näiteks mitte vektorite a → ja b → koordinaadid, vaid nende laiendused vormi koordinaatvektorites b → = b x i → + b y j → + b z k → ja c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → või vektorid a → ja b → saab anda nende koordinaatidega. algus- ja lõpp-punktid.

Mõelge järgmistele näidetele.

Näide 2

Ristkülikukujulises koordinaatsüsteemis on seatud kaks vektorit a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Leidke nende vektorprodukt.

Lahendus

Teise definitsiooni järgi leiame kahe vektori vektorkorrutise antud koordinaatides: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

Kui kirjutada vektorkorrutis läbi maatriksdeterminandi, siis selle näite lahendus on järgmine: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Vastus: a → × b → = - 2 i → - 2 j → - 2 k → .

Näide 3

Leia vektorite i → - j → ja i → + j → + k → ristkorrutise pikkus, kus i → , j → , k → - ristkülikukujulise ristkülikukujulise koordinaatsüsteemi orts.

Lahendus

Kõigepealt leiame antud vektorkorrutise i → - j → × i → + j → + k → koordinaadid antud ristkülikukujulises koordinaatsüsteemis.

On teada, et vektoritel i → - j → ja i → + j → + k → on vastavalt koordinaadid (1 ; - 1 ; 0) ja (1 ; 1 ; 1). Leidke maatriksdeterminandi abil vektorkorrutise pikkus, siis on i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Seetõttu on vektorkorrutisel i → - j → × i → + j → + k → koordinaadid (- 1 ; - 1 ; 2) antud süsteem koordinaadid.

Vektorkorrutise pikkuse leiame valemiga (vt vektori pikkuse leidmise osa): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Vastus: i → - j → × i → + j → + k → = 6 . .

Näide 4

Kolme punkti A (1 , 0 , 1) , B (0 , 2 , 3) ​​, C (1 , 4 , 2) koordinaadid on antud ristkülikukujulises Descartes'i koordinaatide süsteemis. Leia mõni vektor, mis on samaaegselt risti A B → ja A C →.

Lahendus

Vektoritel A B → ja A C → on järgmised koordinaadid (- 1 ; 2 ; 2) ja (0 ; 4 ; 1). Olles leidnud vektorite A B → ja A C → vektorkorrutise, on ilmne, et see on definitsiooni järgi risti vektoriga nii A B → kui ka A C → , st see on meie ülesande lahendus. Leidke see A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Vastus: - 6 i → + j → - 4 k → . on üks risti vektoritest.

Kolmandat tüüpi ülesanded on suunatud vektorite vektorkorrutise omaduste kasutamisele. Pärast mille rakendamist saame antud probleemile lahenduse.

Näide 5

Vektorid a → ja b → on risti ja nende pikkused on vastavalt 3 ja 4. Leidke ristkorrutise pikkus 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Lahendus

Vektorkorrutise jaotusomaduse järgi saame kirjutada 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Assotsiatiivsuse omaduse järgi võtame viimases avaldises välja arvulised koefitsiendid, mis jäävad vektorkorrutise märgist kaugemale: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektorkorrutised a → × a → ja b → × b → on võrdsed 0-ga, kuna a → × a → = a → a → sin 0 = 0 ja b → × b → = b → b → sin 0 = 0 , siis 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

Vektorkorrutise antikommutatiivsusest järeldub - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Vektorkorrutise omadusi kasutades saame võrrandi 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Tingimuse järgi on vektorid a → ja b → risti, st nendevaheline nurk on võrdne π 2 . Nüüd jääb üle vaid asendada leitud väärtused vastavatesse valemitesse: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Vastus: 3 a → - b → × a → - 2 b → = 60 .

Vektorite ristkorrutise pikkus definitsiooni järgi on a → × b → = a → · b → · sin ∠ a → , b → . Kuna see on juba teada (alates koolikursus), et kolmnurga pindala on pool selle kahe külje pikkuste korrutisest antud külgede vahelise nurga siinusega. Seetõttu on vektori korrutise pikkus võrdne rööpküliku pindalaga - kahekordse kolmnurgaga, nimelt külgede korrutisega vektorite a → ja b → kujul, mis on ühest punktist siinuse võrra eraldatud. nendevahelisest nurgast sin ∠ a → , b → .

See on vektorkorrutise geomeetriline tähendus.

Vektorkorrutise füüsikaline tähendus

Mehaanikas, ühes füüsika harudest, saate tänu vektorkorrutisele määrata jõumomendi ruumipunkti suhtes.

3. määratlus

Punktile B rakendatud jõumomendil F → punkti A suhtes saame aru järgmisest vektorkorrutisest A B → × F → .

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Selles õppetükis vaatleme veel kahte vektoritega tehtavat toimingut: vektorite ristkorrutis Ja vektorite segakorrutis (vahetu link neile, kes seda vajavad). Pole hullu, vahel juhtub, et täielikuks õnneks lisaks vektorite punktkorrutis, on vaja järjest rohkem. Selline on vektorsõltuvus. Võib jääda mulje, et oleme sattumas analüütilise geomeetria džunglisse. See on vale. Kõrgema matemaatika selles osas on küttepuid üldiselt vähe, välja arvatud ehk piisavalt Pinocchio jaoks. Tegelikult on materjal väga levinud ja lihtne – vaevalt raskem kui sama skalaarkorrutis, isegi tüüpilisi ülesandeid on vähem. Peamine asi analüütilises geomeetrias, nagu paljud näevad või on juba näinud, on MITTE VEDA ARVUTUSTES. Korrake nagu loitsu ja olete õnnelik =)

Kui vektorid sädelevad kusagil kaugel, nagu välk silmapiiril, siis pole vahet, alusta õppetunniga Mannekeenide vektorid taastada või omandada algteadmised vektorite kohta. Ettevalmistumad lugejad saavad infoga tutvuda valikuliselt, püüdsin kokku koguda võimalikult tervikliku näitekogu, mida sageli leidub praktiline töö

Mis teeb sind õnnelikuks? Kui olin väike, oskasin kahe ja isegi kolme palliga žongleerida. See tuli hästi välja. Nüüd pole üldse vaja žongleerida, kuna me kaalume ainult ruumivektorid, ja kahe koordinaadiga lamevektorid jäetakse välja. Miks? Nii need tegevused sündisid – vektor ja vektorite segakorrutis on defineeritud ja toimivad kolmemõõtmelises ruumis. Juba lihtsam!

Selles toimingus, samamoodi nagu skalaarkorrutis, kaks vektorit. Olgu need kadumatud tähed.

Tegevus ise tähistatud järgmisel viisil: . On ka teisi võimalusi, aga ma olen harjunud vektorite ristkorrutist niimoodi tähistama, nurksulgudes koos ristiga.

Ja kohe küsimus: kui sisse vektorite punktkorrutis kaasatud on kaks vektorit ja siin korrutatakse ka kaks vektorit, siis mis vahe on? Selge erinevus, esiteks TULEMUSES:

Vektorite skalaarkorrutise tulemus on ARV:

Vektorite ristkorrutise tulemus on VEKTOR: , ehk siis korrutame vektorid ja saame uuesti vektori. Suletud klubi. Tegelikult sellest ka operatsiooni nimi. Erinevas õppekirjanduses võivad tähistused samuti erineda, kasutan tähte .

Ristkorrutise määratlus

Kõigepealt tuleb pildiga definitsioon, seejärel kommentaarid.

Definitsioon: risttoode mittekollineaarne vektorid, võetud selles järjekorras, nimetatakse VECTORiks, pikkus mis on arvuliselt võrdne rööpküliku pindalaga, ehitatud nendele vektoritele; vektor vektoritega ortogonaalne, ja on suunatud nii, et alus oleks õiges suunas:

Analüüsime definitsiooni luude kaupa, seal on palju huvitavat!

Seega võime esile tõsta järgmisi olulisi punkte:

1) Lähtevektorid, definitsiooni järgi tähistatud punaste nooltega mitte kollineaarne. Kollineaarsete vektorite juhtumit on asjakohane käsitleda veidi hiljem.

2) Võetud vektorid ranges järjekorras: – "a" korrutatakse arvuga "olla", mitte "olema" asemel "a". Vektori korrutamise tulemus on VECTOR , mis on tähistatud sinisega. Kui vektoreid korrutada vastupidises järjekorras, siis saame vektori, mis on võrdne pikkusega ja vastassuunas (karmiinpunane). See tähendab võrdsust .

3) Nüüd tutvume vektorkorrutise geomeetrilise tähendusega. See on väga oluline punkt! Sinise vektori (ja seega ka karmiinpunase vektori ) PIKKUS on arvuliselt võrdne vektoritele ehitatud rööpküliku PIIRKONNAga. Joonisel on see rööpkülik mustaks varjutatud.

Märge : joonis on skemaatiline ja loomulikult ei võrdu ristkorrutise nimipikkus rööpküliku pindalaga.

Mäletame ühte neist geomeetrilised valemid: rööpküliku pindala on võrdne külgnevate külgede ja nendevahelise nurga siinuse korrutisega. Seetõttu kehtib eelneva põhjal vektorkorrutise PIKKUSE arvutamise valem:

Rõhutan, et valemis räägime vektori PIKKUSEST, mitte vektorist endast. Mis on praktiline tähendus? Ja tähendus on selline, et analüütilise geomeetria probleemide korral leitakse rööpküliku pindala sageli vektorkorrutise kontseptsiooni kaudu:

Võtame korraks oluline valem. Rööpküliku diagonaal (punane punktiirjoon) jagab selle kaheks võrdne kolmnurk. Seetõttu saab vektoritele ehitatud kolmnurga pindala (punane varjutus) leida valemiga:

4) Sama oluline fakt on see, et vektor on vektoritega ortogonaalne, see tähendab . Muidugi on ka vastupidise suunaga vektor (karmiinpunane nool) ortogonaalne algsete vektoritega .

5) Vektor on suunatud nii alus Sellel on õige orientatsiooni. Õppetunnis umbes üleminek uuele alusele Olen sellest üksikasjalikult rääkinud tasapinnaline orientatsioon, ja nüüd selgitame välja, mis on ruumi orientatsioon. Ma selgitan teile sõrmedel parem käsi. Vaimselt kombineerida nimetissõrm vektoriga ja keskmine sõrm vektoriga. Sõrmuse sõrm ja väike sõrm suruge peopessa. Tulemusena pöial- vektorkorrutis otsib üles. See on paremale suunatud alus (see on joonisel). Nüüd vaheta vektorid ( nimetis- ja keskmised sõrmed) mõnes kohas pöördub selle tulemusena pöial ümber ja vektorkorrutis vaatab juba alla. See on ka paremale suunatud alus. Võib-olla on teil küsimus: mis alusel on vasakpoolne orientatsioon? "Määrake" samad sõrmed vasak käsi vektorid ja saate vasakpoolse baasi ja vasakpoolse ruumi orientatsiooni (sel juhul asub pöial alumise vektori suunas). Piltlikult öeldes “väänavad” või orienteerivad need alused ruumi eri suundades. Ja seda kontseptsiooni ei tohiks pidada millekski kaugeks või abstraktseks - näiteks muudab kõige tavalisem peegel ruumi orientatsiooni ja kui "tõmbate peegeldunud objekti peeglist välja", siis üldiselt pole see võimalik ühendage see "originaaliga". Muide, tooge kolm sõrme peegli juurde ja analüüsige peegeldust ;-)

... kui hea on see, et sa sellest nüüd tead paremale ja vasakule orienteeritud alused, sest osade õppejõudude väited orientatsiooni muutumise kohta on kohutavad =)

Kollineaarsete vektorite vektorkorrutis

Definitsioon on üksikasjalikult välja töötatud, jääb üle välja selgitada, mis juhtub, kui vektorid on kollineaarsed. Kui vektorid on kollineaarsed, siis saab need asetada ühele sirgele ja ka meie rööpkülik “voldib” üheks sirgeks. Selliste ala, nagu matemaatikud ütlevad, degenereerunud rööpkülik on null. Sama tuleneb valemist - nulli ehk 180 kraadi siinus võrdub nulliga, mis tähendab, et pindala on null

Seega, kui , siis Ja . Pange tähele, et ristkorrutis ise on võrdne nullvektoriga, kuid praktikas jäetakse see sageli tähelepanuta ja kirjutatakse, et see on samuti võrdne nulliga.

Erijuhtum on vektori ja enda vektorkorrutis:

Ristkorrutise abil saate kontrollida kolmemõõtmeliste vektorite kollineaarsust ja see ülesanne muu hulgas analüüsime ka.

Lahenduste jaoks praktilisi näiteid võib olla vajalik trigonomeetriline tabel siit siinuste väärtuste leidmiseks.

Noh, teeme tuld:

Näide 1

a) Leia vektorite vektorkorrutise pikkus, kui

b) Leidke vektoritele ehitatud rööpküliku pindala, kui

Lahendus: Ei, see pole kirjaviga, muutsin tingimuse üksuste lähteandmed tahtlikult samaks. Sest lahenduste kujundus on erinev!

a) Vastavalt tingimusele on vaja leida pikkus vektor (vektori korrutis). Vastavalt vastavale valemile:

Vastus:

Kuna küsiti pikkuse kohta, siis vastuses märgime mõõtme - ühikud.

b) Vastavalt tingimusele on vaja leida ruut vektoritele ehitatud rööpkülik . Selle rööpküliku pindala on arvuliselt võrdne ristkorrutise pikkusega:

Vastus:

Pange tähele, et vektorkorrutise vastuses pole üldse juttu, meilt küsiti selle kohta figuuri piirkond, mõõde on vastavalt ruutühikud.

Vaatame alati, MIDA tingimus peab leidma, ja selle põhjal sõnastame selge vastama. See võib tunduda sõnasõnalisusena, kuid õpetajate hulgas on piisavalt literaliste ja suure tõenäosusega ülesanne tagastatakse ülevaatamiseks. Kuigi tegemist ei ole eriti pingutatud näpunäidetega – kui vastus on vale, siis jääb mulje, et inimene ei saa lihtsatest asjadest aru ja/või pole ülesande olemusest aru saanud. Seda hetke tuleks alati kontrolli all hoida, lahendades mis tahes ülesandeid kõrgemas matemaatikas ja ka teistes ainetes.

Kuhu kadus suur "en" täht? Põhimõtteliselt võiks selle täiendavalt lahenduse külge kinni jääda, aga rekordi lühendamiseks ma seda ei teinud. Loodan, et kõik saavad sellest aru ja tähistavad sama asja.

Populaarne näide sõltumatu otsus:

Näide 2

Leidke vektoritele ehitatud kolmnurga pindala, kui

Vektorkorrutise kaudu kolmnurga pindala leidmise valem on toodud definitsiooni kommentaarides. Lahendus ja vastus tunni lõpus.

Praktikas on ülesanne tõesti väga levinud, kolmnurki saab üldiselt piinata.

Muude probleemide lahendamiseks vajame:

Vektorite ristkorrutise omadused

Oleme juba vaaginud mõnda vektorprodukti omadust, kuid lisan need sellesse loendisse.

Suvaliste vektorite ja suvalise arvu korral kehtivad järgmised omadused:

1) Teistes teabeallikates seda elementi omadustes tavaliselt ei eristata, kuid see on praktilises mõttes väga oluline. Nii et las olla.

2) - vara on ka ülalpool juttu, vahel nimetatakse antikommutatiivsus. Teisisõnu, vektorite järjekord on oluline.

3) - kombinatsioon või assotsiatiivne vektorkorrutise seadused. Konstandid on kergesti eemaldatavad vektorkorrutise piiridest. Tõesti, mida nad seal teevad?

4) - levitamine või levitamine vektorkorrutise seadused. Ka sulgude avamisega pole probleeme.

Näitena kaaluge lühikest näidet:

Näide 3

Leia, kui

Lahendus: Tingimuse järgi on jällegi vaja leida vektorkorrutise pikkus. Maalime oma miniatuuri:

(1) Vastavalt assotsiatiivsetele seadustele võtame konstandid välja vektorkorrutise piiridest.

(2) Me võtame moodulist välja konstandi, samal ajal kui moodul “sööb” miinusmärgi. Pikkus ei saa olla negatiivne.

(3) Järgnev on selge.

Vastus:

On aeg puid tulle visata:

Näide 4

Arvutage vektoritele ehitatud kolmnurga pindala, kui

Lahendus: leidke valemi abil kolmnurga pindala . Probleem seisneb selles, et vektorid "ce" ja "te" on ise esitatud vektorite summadena. Siinne algoritm on standardne ja meenutab mõneti tunni näiteid nr 3 ja 4. Vektorite punktkorrutis. Selguse huvides jagame selle kolmeks etapiks:

1) Esimeses etapis väljendame vektorprodukti vektorkorrutise kaudu, tegelikult väljendada vektorit vektori kaudu. Pikkuse kohta pole veel sõnagi!

(1) Asendame vektorite avaldised.

(2) Kasutades distributsiooniseadusi, avame sulud polünoomide korrutamise reegli järgi.

(3) Kasutades assotsiatiivseid seadusi, võtame välja kõik konstandid väljaspool vektorkorrutisi. Vähese kogemuse korral saab toiminguid 2 ja 3 teha samaaegselt.

(4) Esimene ja viimane liige on meeldiva omaduse tõttu võrdsed nulliga (nullvektor). Teises terminis kasutame vektori korrutise antikommutatiivsuse omadust:

(5) Esitame sarnased terminid.

Selle tulemusel selgus, et vektor oli väljendatud vektori kaudu, mis oli see, mida oli vaja saavutada:

2) Teises etapis leiame meile vajaliku vektorkorrutise pikkuse. See toiming sarnaneb näitega 3:

3) Leidke vajaliku kolmnurga pindala:

Lahenduse etapid 2-3 võiks olla paigutatud ühele reale.

Vastus:

Vaadeldav probleem on üsna levinud kontrolltööd, siin on näide isetegemise lahendusest:

Näide 5

Leia, kui

Lühilahendus ja vastus tunni lõpus. Vaatame, kui tähelepanelik sa eelmisi näiteid uurides olid ;-)

Vektorite ristkorrutis koordinaatides

, antud ortonormaalses baasis , väljendatakse valemiga:

Valem on tõesti lihtne: determinandi ülemisele reale kirjutame koordinaatvektorid, teisele ja kolmandale reale “pakime” vektorite koordinaadid ja paneme ranges järjekorras- esiteks vektori "ve" koordinaadid, seejärel vektori "double-ve" koordinaadid. Kui vektoreid on vaja korrutada teises järjekorras, tuleb ka read vahetada:

Näide 10

Kontrollige, kas järgmised ruumivektorid on kollineaarsed:
A)
b)

Lahendus: Test põhineb ühel selle õppetunni väitel: kui vektorid on kollineaarsed, siis on nende ristkorrutis null (nullvektor): .

a) Leidke vektorkorrutis:

Seega ei ole vektorid kollineaarsed.

b) Leidke vektorkorrutis:

Vastus a) mitte kollineaarne, b)

Siin on võib-olla kogu põhiteave vektorite vektorkorrutise kohta.

See jaotis ei ole väga suur, kuna vektorite segakorrutise kasutamisel on vähe probleeme. Tegelikult toetub kõik määratlusele, geomeetrilisele tähendusele ja paarile töövalemile.

segatud toode vektorid on kolme vektori korrutis:

Nii rivistusid nad nagu rong ja ootavad, nad ei jõua ära oodata, kuni välja arvutatakse.

Kõigepealt jälle definitsioon ja pilt:

Definitsioon: Segatoode mitte-tasapinnaline vektorid, võetud selles järjekorras, kutsutakse rööptahuka maht, mis on ehitatud nendele vektoritele, varustatud märgiga "+", kui alus on õige, ja märgiga "-", kui alus on vasakpoolne.

Teeme joonistamise. Meile nähtamatud jooned on joonistatud punktiirjoonega:

Sukeldume määratlusse:

2) Võetud vektorid kindlas järjekorras, see tähendab, et vektorite permutatsioon korrutises, nagu võite arvata, ei jää tagajärgedeta.

3) Enne geomeetrilise tähenduse kommenteerimist märgin ära ilmse fakti: vektorite segakorrutis on ARV: . Õppekirjanduses võib kujundus olla mõnevõrra erinev, varem tähistasin segatoodet läbi ja arvutuste tulemust tähega "pe".

A-prioor segaprodukt on rööptahuka ruumala, ehitatud vektoritele (joonis on joonistatud punaste vektorite ja mustade joontega). See tähendab, et arv on võrdne antud rööptahuka helitugevusega.

Märge : Joonis on skemaatiline.

4) Ärme hakka jälle vaeva nägema aluse ja ruumi orientatsiooni mõistega. Lõpuosa tähendus on see, et helitugevusele saab lisada miinusmärgi. Lihtsate sõnadega, võib segatoode olla negatiivne: .

Definitsioonist tuleneb otseselt vektoritele ehitatud rööptahuka ruumala arvutamise valem.