Továbbra is a rendszerekkel foglalkozunk lineáris egyenletek. Eddig olyan rendszerekkel foglalkoztunk, amelyek egyedi megoldással rendelkeznek. Az ilyen rendszerek bármilyen módon megoldhatók: helyettesítési módszer("iskola") Cramer-képletekkel, mátrix módszerrel, Gauss módszer. A gyakorlatban azonban elterjedt még két eset, amikor:

1) a rendszer inkonzisztens (nincs megoldása);

2) a rendszernek végtelen sok megoldása van.

Ezeknél a rendszereknél a leguniverzálisabb megoldási módszereket alkalmazzák - Gauss módszer. Valójában az "iskola" módszer is elvezet a válaszhoz, de a felsőbb matematikában szokás a Gauss-módszert használni az ismeretlenek egymást követő kiküszöbölésére. Aki nem ismeri a Gauss-módszer algoritmust, kérem, először tanulmányozza át a leckét Gauss módszer

Maguk az elemi mátrixtranszformációk pontosan ugyanazok, a különbség a megoldás végén lesz. Először nézzünk meg néhány példát, ahol a rendszernek nincs megoldása (inkonzisztens).

1. példa

Mi az, ami azonnal megakad ebben a rendszerben? Az egyenletek száma kevesebb, mint a változók száma. Van egy tétel, ami azt mondja: „Ha a rendszerben az egyenletek száma kevesebb, mint a változók száma, akkor a rendszer vagy inkonzisztens, vagy végtelen sok megoldása van.És már csak ki kell deríteni.

A megoldás eleje teljesen hétköznapi - felírjuk a rendszer kiterjesztett mátrixát, és elemi transzformációkkal lépésenkénti formába hozzuk:

(1). A bal felső lépésben (+1) vagy (-1) kell kapnunk. Az első oszlopban nincsenek ilyen számok, így a sorok átrendezése nem fog működni. Az egységet önállóan kell megszervezni, és ez többféleképpen is megtehető. Így tettünk. Az első sorhoz hozzáadjuk a harmadik sort (-1) megszorozva.

(2). Most két nullát kapunk az első oszlopban. A második sorhoz adja hozzá az első sort 3-mal szorozva. A harmadik sorhoz adja hozzá az elsőt 5-tel.

(3). Az átalakítás után mindig érdemes megnézni, hogy lehet-e egyszerűsíteni a kapott karakterláncokat? Tud. A második sort elosztjuk 2-vel, ezzel egyidejűleg a második lépésben megkapjuk a kívántat (-1). Osszuk el a harmadik sort (-3)-mal.

(4). Adja hozzá a második sort a harmadikhoz. Valószínűleg mindenki felfigyelt a rossz vonalra, amely az elemi átalakítások eredményeként alakult ki:

. Nyilvánvaló, hogy ez nem lehet így.

Valójában átírjuk a kapott mátrixot

vissza a lineáris egyenletrendszerhez:

Ha elemi transzformációk eredményeként egy karakterlánc az alak , Aholλ egy nem nulla szám, akkor a rendszer inkonzisztens (nincs megoldása).

Hogyan rögzítsük egy feladat végét? Le kell írnia a következő mondatot:

„Elemi transzformációk eredményeként egy olyan alakzatot kapunk, ahol λ ≠ 0 ". Válasz: "A rendszernek nincsenek megoldásai (inkonzisztens)."

Kérjük, vegye figyelembe, hogy ebben az esetben a Gauss-algoritmusnak nincs fordított mozgása, nincsenek megoldások és egyszerűen nincs mit találni.

2. példa

Oldjon meg egy lineáris egyenletrendszert!

Ez egy példa erre független megoldás. Komplett megoldásés a válasz a lecke végén.

Ismételten emlékeztetünk arra, hogy az Ön megoldási folyamata eltérhet a mi megoldási folyamatunktól, a Gauss-módszer nem határoz meg egyértelmű algoritmust, az eljárást és magukat a műveleteket minden esetben egymástól függetlenül kell kitalálnia.

Másik műszaki jellemző megoldások: az elemi transzformációk leállíthatók Egyszerre, amint egy sort, mint , hol λ ≠ 0 . Vegyünk egy feltételes példát: tegyük fel, hogy az első transzformáció után kapunk egy mátrixot

.

Ez a mátrix még nem redukálódott lépcsőzetes formává, de nincs szükség további elemi átalakításokra, hiszen megjelent az űrlap egy sora, ahol λ ≠ 0 . Azonnal azt kell válaszolni, hogy a rendszer nem kompatibilis.

Ha egy lineáris egyenletrendszernek nincs megoldása, ez szinte ajándék a tanulónak, mert rövid megoldás születik, néha szó szerint 2-3 lépésben. De ezen a világon minden kiegyensúlyozott, és a probléma, amelyre a rendszernek végtelenül sok megoldása van, csak hosszabb.

3. példa:

Oldjon meg egy lineáris egyenletrendszert!

4 egyenlet és 4 ismeretlen, tehát a rendszernek vagy egyetlen megoldása lehet, vagy nincs megoldása, vagy végtelen sok megoldása lehet. Bármi is volt, de a Gauss-módszer mindenképpen elvezet minket a válaszhoz. Ez a sokoldalúsága.

Az eleje ismét szabványos. Felírjuk a rendszer kiterjesztett mátrixát, és elemi transzformációkkal lépésformára hozzuk:

Ez minden, és féltél.

(1). Kérjük, vegye figyelembe, hogy az első oszlopban lévő összes szám osztható 2-vel, így a bal felső lépésben is megelégszünk egy kettessel. A második sorhoz hozzáadjuk az első sort (-4) megszorozva. A harmadik sorhoz hozzáadjuk az első sort (-2) megszorozva. A negyedik sorhoz hozzáadjuk az első sort (-1) megszorozva.

Figyelem! Sokan kísértésbe eshetnek a negyedik sorból kivonni első sor. Ezt meg lehet tenni, de nem szükséges, a tapasztalat azt mutatja, hogy a számítási hiba valószínűsége többszörösére nő. Csak összeadjuk: a negyedik sorhoz hozzáadjuk az első sort, megszorozva (-1) - pontosan!

(2). Az utolsó három sor arányos, ebből kettő törölhető. Itt ismét meg kell mutatni fokozott figyelem, de tényleg arányosak a vonalak? A viszontbiztosításhoz nem lesz felesleges a második sort megszorozni (-1) és a negyedik sort elosztani 2-vel, ami három azonos sort eredményez. És csak ezután távolítson el kettőt. Az elemi átalakítások eredményeként a rendszer kiterjesztett mátrixa lépcsőzetes formára redukálódik:

A feladat füzetben való elkészítésekor az áttekinthetőség kedvéért célszerű ugyanezeket a jegyzeteket ceruzával elkészíteni.

Átírjuk a megfelelő egyenletrendszert:

A rendszer „szokásos” egyetlen megoldásának itt nincs szaga. Rossz vonal hol λ ≠ 0, szintén nem. Ezért ez a harmadik fennmaradó eset – a rendszernek végtelen sok megoldása van.

A rendszer végtelen megoldáshalmazát röviden az ún általános rendszermegoldás.

A rendszer általános megoldását a Gauss-módszer fordított mozgásával fogjuk megtalálni. A végtelen megoldáshalmazt tartalmazó egyenletrendszereknél új fogalmak jelennek meg: "alapváltozók"És "szabad változók". Először is határozzuk meg, milyen változóink vannak alapvető, és milyen változók - ingyenes. Nem szükséges részletesen elmagyarázni a lineáris algebra feltételeit, elég megjegyezni, hogy vannak ilyenek bázisváltozókÉs szabad változók.

Az alapváltozók mindig szigorúan a mátrix lépésein „ülnek”.. Ebben a példában az alapváltozók a következők x 1 és x 3 .

A szabad változók minden többi változók, amelyek nem kaptak lépést. A mi esetünkben kettő van: x 2 és x 4 - szabad változók.

Most kell Mindenbázisváltozók Expressz csak keresztülszabad változók. A Gauss-algoritmus fordított mozgása hagyományosan alulról felfelé működik. A rendszer második egyenletéből fejezzük ki az alapváltozót x 3:

Most nézzük meg az első egyenletet: . Először behelyettesítjük a talált kifejezést:

Marad az alapváltozó kifejezése x 1-től szabad változókon keresztül x 2 és x 4:

Az eredmény az, amire szüksége van - Minden bázisváltozók ( x 1 és x 3) kifejezve csak keresztül szabad változók ( x 2 és x 4):

Valójában az általános megoldás készen áll:

.

Hogyan írjuk le az általános megoldást? Először is a szabad változókat „önmagukban” és szigorúan a helyükre írjuk be az általános megoldásba. Ebben az esetben a szabad változók x 2 és x A 4-et a második és a negyedik pozícióba kell írni:

.

Az eredményül kapott kifejezések az alapváltozókhoz és nyilvánvalóan az első és a harmadik pozícióba kell írni:

A rendszer általános megoldásából végtelenül sok megtalálható privát döntések. Ez nagyon egyszerű. szabad változók x 2 és x 4 azért hívják így, mert megadható bármilyen végső értéket. A legnépszerűbb értékek a nulla értékek, mivel ez a legegyszerűbb módja egy adott megoldás megszerzésének.

Behelyettesítés ( x 2 = 0; x 4 = 0) az általános megoldásba, az egyik konkrét megoldást kapjuk:

, vagy egy adott megoldás a szabad változóknak megfelelő értékekkel ( x 2 = 0; x 4 = 0).

Egyik egy másik édes pár, helyettesítsük ( x 2 = 1 és x 4 = 1) az általános megoldásba:

, azaz a (-1; 1; 1; 1) egy másik sajátos megoldás.

Könnyen belátható, hogy az egyenletrendszer rendelkezik végtelenül sok megoldás hiszen szabad változókat adhatunk Bármiértékeket.

Minden egyes egy adott megoldásnak meg kell felelnie mindenkinek rendszeregyenlet. Ez az alapja a megoldás helyességének „gyors” ellenőrzésének. Vegyünk például egy adott megoldást (-1; 1; 1; 1), és cseréljük be az eredeti rendszerben minden egyenlet bal oldalába:

Mindennek össze kell jönnie. És minden adott megoldásnál mindennek konvergálnia kell.

Szigorúan véve egy adott megoldás verifikációja néha megtéveszt, i.e. egy adott megoldás kielégítheti a rendszer minden egyenletét, és magát az általános megoldást valójában helytelenül találjuk meg. Ezért mindenekelőtt az általános megoldás ellenőrzése alaposabb és megbízhatóbb.

Hogyan ellenőrizhető a kapott általános megoldás ?

Nem nehéz, de elég hosszú átalakítást igényel. Kifejezéseket kell vennünk alapvető változók, ebben az esetben és , és cserélje be őket a rendszer minden egyenletének bal oldalára.

A rendszer első egyenletének bal oldalán:

Megkapjuk a rendszer eredeti első egyenletének jobb oldalát.

A rendszer második egyenletének bal oldalán:

Megkapjuk a rendszer eredeti második egyenletének jobb oldalát.

És tovább - a rendszer harmadik és negyedik egyenletének bal oldalára. Ez az ellenőrzés hosszabb, de garantálja a teljes megoldás 100%-os helyességét. Ezenkívül bizonyos feladatoknál ellenőrizni kell az általános megoldást.

4. példa:

Oldja meg a rendszert Gauss módszerrel! Keressen egy általános és két privát megoldást. Ellenőrizze az általános megoldást.

Ez egy „csináld magad” példa. Itt egyébként megint kevesebb az egyenletek száma, mint az ismeretleneké, ami azt jelenti, hogy azonnal világos, hogy a rendszer vagy inkonzisztens lesz, vagy végtelen számú megoldással.

5. példa:

Oldjon meg egy lineáris egyenletrendszert! Ha a rendszernek végtelen sok megoldása van, keressen két konkrét megoldást, és ellenőrizze az általános megoldást

Megoldás:Írjuk fel a rendszer kiterjesztett mátrixát, és elemi transzformációk segítségével hozzuk lépcsőzetes formába:

(1). Adja hozzá az első sort a másodikhoz. A harmadik sorhoz hozzáadjuk az első sort 2-vel szorozva. A negyedik sorhoz hozzáadjuk az első sort 3-mal szorozva.

(2). A harmadik sorhoz hozzáadjuk a második sort (-5) megszorozva. A negyedik sorhoz hozzáadjuk a második sort (-7) megszorozva.

(3). A harmadik és a negyedik sor megegyezik, az egyiket töröljük. Íme egy ilyen szépség:

Az alapváltozók lépcsőkön helyezkednek el, tehát alapváltozók.

Csak egy szabad változó van, amely nem kapott lépést: .

(4). Fordított mozgás. Az alapváltozókat a szabad változóval fejezzük ki:

A harmadik egyenletből:

Tekintsük a második egyenletet, és cseréljük be a talált kifejezést:

, , ,

Tekintsük az első egyenletet, és helyettesítsük be a talált kifejezéseket és ebbe:

Így az általános megoldás egy szabad változóval x 4:

Még egyszer, hogyan történt? szabad változó x 4 egyedül áll a jogos negyedik helyen. A , , alapváltozókra kapott kifejezések szintén a helyükön vannak.

Azonnal ellenőrizzük az általános megoldást.

A , , alapváltozókat behelyettesítjük a rendszer minden egyenletének bal oldalába:

Az egyenletek megfelelő jobb oldalait megkapjuk, így megtaláljuk a helyes általános megoldást.

Most a megtalált általános megoldásból két konkrét megoldást kapunk. Itt minden változót egyetlenegyen keresztül fejezünk ki szabad x változó 4. Nem kell törni a fejét.

Hadd x 4 = 0, akkor az első konkrét megoldás.

Hadd x 4 = 1, akkor egy másik speciális megoldás.

Válasz: Közös döntés: . Privát megoldások:

És .

6. példa:

Keresse meg a lineáris egyenletrendszer általános megoldását!

Az általános megoldást már ellenőriztük, a válaszban megbízhatunk. Az Ön intézkedései eltérhetnek a mi cselekvéseinktől. A lényeg, hogy az általános megoldások egybeesjenek. Valószínűleg sokan észrevettek egy kellemetlen momentumot a megoldásokban: nagyon gyakran a Gauss-módszer fordított lefolyása során kellett babrálni. közönséges törtek. A gyakorlatban ez igaz, sokkal ritkábban fordulnak elő olyan esetek, amikor nincs tört. Legyen felkészült lelkileg, és ami a legfontosabb, technikailag.

Maradjunk a megoldás azon jellemzőinél, amelyek a megoldott példákban nem szerepeltek. A rendszer általános megoldása néha tartalmazhat konstanst (vagy állandókat).

Például az általános megoldás: . Itt az egyik alapváltozó egy állandó számmal egyenlő: . Ebben nincs semmi egzotikus, előfordul. Nyilvánvaló, hogy ebben az esetben minden konkrét megoldás ötöst tartalmaz az első helyen.

Ritkán, de vannak olyan rendszerek, amelyekben egyenletek száma több mennyiséget változók. A Gauss-módszer azonban a legsúlyosabb körülmények között is működik. A rendszer kiterjesztett mátrixát nyugodtan hozd lépcsőzetes formába a szabványos algoritmus szerint. Lehet, hogy egy ilyen rendszer inkonzisztens, végtelenül sok megoldást tartalmazhat, és furcsa módon egyedi megoldása is lehet.

Tanácsunkban megismételjük - annak érdekében, hogy kényelmesen érezze magát egy rendszer Gauss-módszerrel történő megoldása során, meg kell töltenie a kezét, és legalább egy tucat rendszert kell megoldania.

Megoldások és válaszok:

2. példa:

Megoldás:Írjuk fel a rendszer kiterjesztett mátrixát, és elemi transzformációkkal hozzuk lépcsőzetes formába.

Elvégzett elemi átalakítások:

(1) Az első és a harmadik sor felcserélődött.

(2) Az első sort hozzáadtuk a másodikhoz, megszorozva (-6)-tal. Az első sort hozzáadtuk a harmadikhoz, megszorozva (-7)-tel.

(3) A második sort hozzáadtuk a harmadikhoz, megszorozva (-1)-gyel.

Az elemi átalakítások eredményeként egy alakzat sztring, Ahol λ ≠ 0 .Tehát a rendszer inkonzisztens.Válasz: nincsenek megoldások.

4. példa:

Megoldás:Felírjuk a rendszer kiterjesztett mátrixát, és elemi transzformációkkal lépésformára hozzuk:

Végrehajtott konverziók:

(1). Az első sort 2-vel szorozva hozzáadtuk a másodikhoz, az első sort 3-mal szorozva a harmadikhoz.

A második lépéshez nincs egység , és a transzformáció (2) annak megszerzésére irányul.

(2). A második sort hozzáadtuk a harmadikhoz, megszorozva -3-mal.

(3). A második és a harmadik sor felcserélődött (az eredményül kapott -1 átkerült a második lépésbe)

(4). A harmadik sorhoz adja hozzá a második sort 3-mal megszorozva.

(5). Az első két sor előjele megváltozott (-1-gyel szorozva), a harmadik sort elosztottuk 14-gyel.

Fordított mozgás:

(1). Itt az alapvető változók (amelyek a lépéseken vannak), és szabad változók (aki nem kapta meg a lépést).

(2). Az alapváltozókat szabad változókkal fejezzük ki:

A harmadik egyenletből: .

(3). Tekintsük a második egyenletet:, speciális megoldások:

Válasz: Közös döntés:

Komplex számok

Ebben a részben bemutatjuk a koncepciót összetett szám, fontolgat algebrai, trigonometrikusÉs forma megjelenítéseösszetett szám. Megtanuljuk továbbá a komplex számokkal végzett műveletek végrehajtását: összeadás, kivonás, szorzás, osztás, hatványozás és gyökkivonás.

A fejlődéshez komplex számok a felsőfokú matematika tantárgyból nem igényel speciális ismereteket, az anyag még egy iskolás számára is elérhető. Elég ahhoz, hogy képes legyen algebrai műveletek"közönséges" számokkal, és ne feledje a trigonometriát.

Először is emlékezzünk a „közönséges” számokra. A matematikában úgy hívják valós számok halmazaés betűvel vannak jelölve R, vagy R (vastag). Minden valós szám az ismerős számsoron található:

A valós számok társasága nagyon színes - itt vannak egész számok, törtek és irracionális számok. Ebben az esetben a numerikus tengely minden pontja szükségszerűen megfelel valamilyen valós számnak.

M lineáris egyenletrendszer n ismeretlennel formarendszernek nevezzük

Ahol aijÉs b i (én=1,…,m; b=1,…,n) néhány ismert szám, és x 1,…,x n- ismeretlen. Az együtthatók jelölésében aij első index én jelöli az egyenlet számát, a másodikat j az ismeretlen száma, amelyen ez az együttható áll.

Az ismeretlenek együtthatói mátrix formájában lesznek felírva 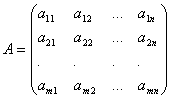, amit hívni fogunk rendszermátrix.

Az egyenletek jobb oldalán található számok b 1 ,…,b m hívott ingyenes tagok.

Összesített n számok c 1 ,…,c n hívott döntés ennek a rendszernek, ha a rendszer minden egyenlete egyenlőséggé válik, miután számokat helyettesítünk bele c 1 ,…,c n a megfelelő ismeretlenek helyett x 1,…,x n.

A mi feladatunk az lesz, hogy megoldásokat találjunk a rendszerre. Ebben az esetben három helyzet állhat elő:

Olyan lineáris egyenletrendszert nevezünk, amelynek legalább egy megoldása van közös. Ellenkező esetben pl. ha a rendszernek nincsenek megoldásai, akkor ún összeegyeztethetetlen.

Fontolja meg, hogyan találhat megoldást a rendszerre.

MÁTRIX MÓDSZER LINEÁRIS EGYENLETRENDSZER MEGOLDÁSÁRA

A mátrixok lehetővé teszik egy lineáris egyenletrendszer rövid leírását. Adjunk meg egy három egyenletrendszert három ismeretlennel:

Tekintsük a rendszer mátrixát valamint ismeretlen és szabad tagok mátrixoszlopai

Keressük meg a terméket

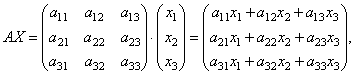
azok. a szorzat eredményeként megkapjuk ennek a rendszernek az egyenleteinek bal oldalát. Ekkor a mátrixegyenlőség definícióját használva ez a rendszer így írható fel

vagy rövidebb A∙X=B.

Itt a mátrixok AÉs B ismertek, és a mátrix x ismeretlen. Meg kell találni, mert. elemei ennek a rendszernek a megoldása. Ezt az egyenletet ún mátrix egyenlet.

Legyen a mátrix determináns különbözik nullától | A| ≠ 0. Ekkor a mátrixegyenletet a következőképpen oldjuk meg. Szorozzuk meg a bal oldali egyenlet mindkét oldalát a mátrixszal A-1, a mátrix inverze A: . Mert a A -1 A = EÉs E∙X=X, akkor a mátrixegyenlet megoldását a formában kapjuk meg X = A -1 B .

Megjegyzendő, hogy mivel az inverz mátrix csak négyzetes mátrixokra található, a mátrixmódszer csak azokat a rendszereket tudja megoldani, amelyekben az egyenletek száma megegyezik az ismeretlenek számával. A rendszer mátrixos jelölése azonban lehetséges abban az esetben is, ha az egyenletek száma nem egyenlő az ismeretlenek számával, akkor a mátrix A nem négyzet alakú, és ezért lehetetlen megoldást találni a rendszerre a formában X = A -1 B.

Példák. Egyenletrendszerek megoldása.

CRAMER SZABÁLYA

Tekintsünk egy 3 lineáris egyenletrendszert három ismeretlennel:

A rendszer mátrixának megfelelő harmadrendű determináns, azaz. ismeretlenek együtthatóiból áll,

hívott rendszer meghatározó.

További három determinánst állítunk össze a következőképpen: a D determinánsban egymás után 1, 2 és 3 oszlopot cserélünk szabad tagokból álló oszlopra.

Ekkor a következő eredményt tudjuk bizonyítani.

Tétel (Cramer-szabály). Ha a rendszer determinánsa Δ ≠ 0, akkor a vizsgált rendszernek csak egy megoldása van, és

Bizonyíték. Tehát vegyünk egy három egyenletből álló rendszert három ismeretlennel. Szorozzuk meg a rendszer 1. egyenletét az algebrai komplementerrel A 11 elem egy 11, 2. egyenlet - be A21és 3. - on A 31:

Adjuk hozzá ezeket az egyenleteket:

Tekintsük ennek az egyenletnek mindegyik zárójelét és jobb oldalát. A determináns 1. oszlop elemei szerinti kiterjesztésének tételével

Hasonlóképpen kimutatható, hogy és .

Végül is ezt könnyű belátni

Így megkapjuk az egyenlőséget: .

Ennélfogva, .

A és egyenlőségeket hasonlóan származtatjuk, ahonnan a tétel állítása következik.

Így megjegyezzük, hogy ha a rendszer determinánsa Δ ≠ 0, akkor a rendszernek egyedi megoldása van, és fordítva. Ha a rendszer determinánsa egyenlő nullával, akkor a rendszernek vagy végtelen megoldáshalmaza van, vagy nincs megoldása, pl. összeegyeztethetetlen.

Példák. Egyenletrendszer megoldása

GAUSS MÓDSZER

A korábban vizsgált módszerekkel csak azokat a rendszereket lehet megoldani, amelyekben az egyenletek száma egybeesik az ismeretlenek számával, és a rendszer determinánsának nullától eltérőnek kell lennie. A Gauss-módszer univerzálisabb, és tetszőleges számú egyenletű rendszerekhez alkalmas. Ez abból áll, hogy a rendszer egyenleteiből egymást követően ki kell zárni az ismeretleneket.

Tekintsünk ismét egy három egyenletrendszert három ismeretlennel:

.

Az elsõ egyenletet változatlanul hagyjuk, a 2. és 3. egyenletbõl pedig kizárjuk a tartalmazó kifejezéseket x 1. Ehhez elosztjuk a második egyenletet A 21 és szorozzuk meg - A 11, majd add össze az 1. egyenlettel. Hasonlóképpen felosztjuk a harmadik egyenletet is A 31 és szorozzuk meg - A 11, majd add hozzá az elsőhöz. Ennek eredményeként az eredeti rendszer a következő formában lesz:

Most az utolsó egyenletből kiküszöböljük a tartalmazó kifejezést x2. Ehhez osszuk el a harmadik egyenletet -vel, szorozzuk meg és adjuk hozzá a másodikhoz. Ekkor lesz egy egyenletrendszerünk:

Ezért az utolsó egyenletből könnyű megtalálni x 3, majd a 2. egyenletből x2és végül 1-től - x 1.

A Gauss-módszer alkalmazásakor az egyenletek szükség esetén felcserélhetők.

Gyakran ahelyett, hogy új egyenletrendszert írnának fel, a rendszer kiterjesztett mátrixának kiírására szorítkoznak:

majd elemi transzformációk segítségével hozza háromszög vagy átló formába.

NAK NEK elemi átalakulások A mátrixok a következő transzformációkat tartalmazzák:

1. sorok vagy oszlopok permutációja;
2. egy karakterlánc szorzása nullától eltérő számmal;
3. egy sorhoz további sorokat ad.

Példák: Egyenletrendszerek megoldása Gauss módszerrel.

Így a rendszernek végtelen számú megoldása van.

5. szakasz: A LINEÁRIS ALGEBRA ELEMEI

Lineáris egyenletrendszerek

Alapfogalmak

Lineáris algebrai egyenletrendszer, tartalmazó T egyenletek és P ismeretlen, formarendszernek nevezzük

hol vannak a számok A ij , én=
, j= hívott együtthatók rendszerek, számok b én - ingyenes tagok. Megtalálandó szám x P .

Kényelmes egy ilyen rendszert kompaktba írni mátrix forma
.

Itt A a rendszer együtthatómátrixa, ún fő mátrix:

,

-ismeretlenek oszlopvektora x j , a szabad tagok oszlopvektora b én .

Kiterjedt a rendszer mátrixa a mátrix rendszer, kiegészítve egy szabad kifejezések rovatával

.

Döntés rendszert hívják P ismeretlen értékek x 1 =c 1 , X 2 =c 2 , ..., X P =c P , amelyek behelyettesítésekor a rendszer összes egyenlete valódi egyenlőséggé válik. A rendszer bármely megoldása felírható mátrixoszlopként .

Az egyenletrendszert ún közös ha van legalább egy megoldása, és összeegyeztethetetlen ha nincs megoldása.

Az ízületi rendszert ún bizonyos ha egyedi megoldása van, és bizonytalan ha egynél több megoldása van. Ez utóbbi esetben mindegyik megoldását ún magándöntés rendszerek. Az összes konkrét megoldás halmazát ún általános megoldás.

Oldja meg a rendszert ez azt jelenti, hogy ki kell deríteni, hogy kompatibilis-e vagy sem. Ha a rendszer konzisztens, akkor keresse meg az általános megoldást.

A két rendszert ún egyenértékű(egyenértékű), ha ugyanaz az általános megoldás. Más szóval, a rendszerek akkor ekvivalensek, ha az egyik megoldása a másik megoldása, és fordítva.

Egyenértékű rendszereket különösen akkor kapunk, ha elemi átalakulások rendszerben, feltéve, hogy a transzformációkat csak a mátrix sorain hajtjuk végre.

A lineáris egyenletrendszert ún homogén ha minden szabad feltétel nulla:

A homogén rendszer mindig konzisztens, hiszen x 1 =x 2 =…=x P =0 a megoldás a rendszerre. Ezt a megoldást ún nulla vagy jelentéktelen.

Lineáris egyenletrendszerek megoldása

Legyen egy tetszőleges rendszer adott T lineáris egyenletek -val P ismeretlen

1. tétel(Kronecker-Cappelli). A lineáris algebrai egyenletrendszer akkor és csak akkor konzisztens, ha a kiterjesztett mátrix rangja megegyezik a főmátrix rangjával.

2. tétel. Ha egy konzisztens rendszer rangja egyenlő az ismeretlenek számával, akkor a rendszernek egyedi megoldása van.

3. tétel. Ha egy konzisztens rendszer rangja kisebb, mint az ismeretlenek száma, akkor a rendszernek végtelen számú megoldása van.

PÉLDA Vizsgálja meg a rendszer kompatibilitását

Megoldás.
,r(A)=1;
, r()=2,
.

És így, r(A) r(), ezért a rendszer inkonzisztens.

Nem degenerált lineáris egyenletrendszerek megoldása. Cramer-képletek

Hagyja a rendszert P lineáris egyenletek -val P ismeretlen

vagy mátrix formában A∙X=B.

Egy ilyen rendszer A fő mátrixa négyzet. Ennek a mátrixnak a determinánsát ún rendszer meghatározó. Ha a rendszer determinánsa nem nulla, akkor a rendszer meghívásra kerül nem degenerált.

Keressük ennek az egyenletrendszernek a megoldását ∆0 esetén. a bal oldali А∙Х=В egyenlet mindkét oldalát megszorozva a А  1 mátrixszal, А  1 ∙ A∙Х= A  1 ∙B kapjuk. Mivel A - 1 ∙ A \u003d E és E ∙ X \u003d X, akkor X \u003d A - 1 ∙ B. A rendszer megoldásának ezt a módszerét az ún. mátrix.

A mátrix módszerből következzen Cramer-képletek
, ahol ∆ a rendszer főmátrixának determinánsa, és ∆ én a ∆ determinánsból cserével kapott determináns én az együtthatók oszlopát a szabad tagok oszlopával.

PÉLDA Oldja meg a rendszert

Megoldás.
, 70,
,
. Eszközök, x 1 =, X 2 =
.

Lineáris egyenletrendszerek megoldása Gauss-módszerrel

A Gauss-módszer az ismeretlenek egymást követő eliminálásából áll.

Legyen az egyenletrendszer

A Gauss-féle megoldási folyamat két lépésből áll. Az első szakaszban (előrefutás) a rendszer redukálódik lépett(különösen, háromszög alakú) ész.

Ahol k≤ n, a ii  0, én= . Esély A ii hívott fő- a rendszer elemei.

A második szakaszban (fordított mozgás) szekvenciálisan meghatározzák az ismeretleneket ebből a lépcsőzetes rendszerből.

Megjegyzések:

Ha a lépésrendszer háromszögletűnek bizonyul, pl. k= n, akkor az eredeti rendszernek egyedi megoldása van. Az utolsó egyenletből azt találjuk x P , az utolsó előtti egyenletből azt találjuk x P  1 , majd felfelé haladva a rendszerben megtaláljuk az összes többi ismeretlent.

A gyakorlatban kényelmesebb a rendszer kiterjesztett mátrixával dolgozni, minden elemi transzformációt végrehajtva annak sorain. Kényelmes, hogy az együttható A 11 egyenlő volt 1-gyel (rendezzük át az egyenleteket, vagy osszuk el A 11 1).

PÉLDA Oldja meg a rendszert Gauss módszerrel!

Megoldás. A rendszer kiterjesztett mátrixa feletti elemi transzformációk eredményeként

~
~
~

~

az eredeti rendszert lépcsőzetessé redukálták:

Ezért a rendszer általános megoldása a következő: x 2 =5 x 4  13 x 3  3; x 1 =5 x 4  8 x 3  1.

Ha feltesszük pl. x 3 =x 4 =0, akkor megtaláljuk ennek a rendszernek az egyik sajátos megoldását x 1 =  1, x 2 =  3, x 3 =0, x 4 =0.

Homogén lineáris egyenletrendszerek

Legyen adott a lineáris homogén egyenletrendszer

Nyilván egy homogén rendszer mindig kompatibilis, van nulla (triviális) megoldása.

4. tétel. Ahhoz, hogy egy homogén egyenletrendszernek nullától eltérő megoldása legyen, szükséges és elegendő, hogy főmátrixának rangja kisebb legyen, mint az ismeretlenek száma, azaz. r< n.

5. tétel. A homogén rendszer érdekében P lineáris egyenletek -val P az ismeretleneknek nullától eltérő megoldása van, szükséges és elégséges, hogy főmátrixának determinánsa nullával egyenlő, azaz. ∆=0.

Ha a rendszer nullától eltérő megoldásokkal rendelkezik, akkor ∆=0.

PÉLDA Oldja meg a rendszert

Megoldás.
,r(A)=2
, n=3. Mert r< n, akkor a rendszernek végtelen számú megoldása van.

,
. vagyis x 1 == 2x 3 , X 2 == 3x 3 - közös döntés.

Elhelyezés x 3 =0, egy konkrét megoldást kapunk: x 1 =0, x 2 =0, x 3 =0. Elhelyezés x 3 =1, megkapjuk a második konkrét megoldást: x 1 =2, x 2 =3, x 3 =1 stb.

Irányítandó kérdések

Mi az a lineáris algebrai egyenletrendszer?

Magyarázza meg a következő fogalmakat: együttható, metszéspont, fő- és kiterjesztett mátrix!

Mik azok a lineáris egyenletrendszerek? Fogalmazzuk meg a Kronker-Capelli tételt (a lineáris egyenletrendszer kompatibilitásáról).

Sorolja fel és magyarázza el a lineáris egyenletrendszerek megoldási módszereit!

Szolgálati megbízás. Az online számológépet lineáris egyenletrendszer tanulmányozására tervezték. Általában a probléma állapotában kell megtalálni a rendszer általános és sajátos megoldása. A lineáris egyenletrendszerek tanulmányozása során a következő problémákat kell megoldani:

1. hogy a rendszer együttműködő-e;
2. ha a rendszer konzisztens, akkor határozott vagy határozatlan (a rendszerkompatibilitás kritériumát a tétel határozza meg);
3. ha a rendszer definiált, akkor hogyan találjuk meg egyedi megoldását (a Cramer-módszert, az inverz mátrix módszert vagy a Jordan-Gauss-módszert használják);
4. ha a rendszer határozatlan, akkor hogyan írjuk le a megoldásainak halmazát.

Lineáris egyenletrendszerek osztályozása

Egy tetszőleges lineáris egyenletrendszer alakja:
a 1 1 x 1 + a 1 2 x 2 + ... + a 1 n x n = b 1
a 2 1 x 1 + a 2 2 x 2 + ... + a 2 n x n = b 2
...................................................
a m 1 x 1 + a m 2 x 2 + ... + a m n x n = b m

1. Lineáris inhomogén egyenletrendszerek (a változók száma megegyezik az egyenletek számával, m = n).
2. Tetszőleges lineáris inhomogén egyenletrendszerek (m > n vagy m< n).

Meghatározás. Egy rendszer megoldása a c 1 ,c 2 ,...,c n számok tetszőleges gyűjteménye, amelynek a rendszerbe való behelyettesítése a megfelelő ismeretlenek helyett a rendszer minden egyenletét azonossággá változtatja.

Meghatározás. Két rendszert egyenértékűnek mondunk, ha az első megoldása a második megoldása, és fordítva.

Meghatározás. Az olyan rendszert, amelynek legalább egy megoldása van, ún közös. Az olyan rendszert, amelynek nincs megoldása, inkonzisztensnek nevezzük.

Meghatározás. Egy egyedi megoldású rendszert ún bizonyos, és ha több megoldás is van, az határozatlan.

Algoritmus lineáris egyenletrendszerek megoldására

1. Keresse meg a fő és a kiterjesztett mátrixok rangsorait! Ha ezek nem egyenlőek, akkor a Kronecker-Capelli-tétel szerint a rendszer inkonzisztens, és itt a vizsgálat véget ér.
2. Legyen rang(A) = rang(B) . Kiválasztjuk az alapmollt. Ebben az esetben az összes ismeretlen lineáris egyenletrendszer két osztályra oszlik. Azokat az ismeretleneket, amelyek együtthatói benne vannak az alapmollban, függőnek, az ismeretleneket pedig, amelyek együtthatói az alapmollban nem szerepelnek, szabadnak nevezzük. Vegye figyelembe, hogy a függő és szabad ismeretlenek kiválasztása nem mindig egyedi.
3. Áthúzzuk a rendszer azon egyenleteit, amelyek együtthatói nem szerepeltek a bázis-mollban, mivel ezek a többi következményei (az alapmoll tétel szerint).
4. A szabad ismeretleneket tartalmazó egyenletek feltételei átkerülnek a jobb oldalra. Ennek eredményeként egy r egyenletrendszert kapunk, amelyben r ismeretlen, ekvivalens az adott egyenletnek, amelynek determinánsa különbözik nullától.
5. Az így kapott rendszert a következő módok egyikével oldjuk meg: Cramer módszerrel, inverz mátrix módszerrel vagy Jordan-Gauss módszerrel. Olyan kapcsolatokat találunk, amelyek a függő változókat a szabad változókkal fejezik ki.

Meghatározás. Rendszer m n ismeretlent tartalmazó egyenletek Általános nézet a következőképpen van írva:

Ahol aij együtthatók, és b i- állandó.

A rendszer megoldásai az n számok, amelyek a rendszerbe behelyettesítve minden egyenletét azonossággá alakítják.

Meghatározás. Ha egy rendszernek van legalább egy megoldása, akkor azt konzisztensnek nevezzük. Ha a rendszernek nincs megoldása, akkor inkonzisztensnek nevezzük.

Meghatározás. Egy rendszert határozottnak nevezünk, ha csak egy megoldása van, és határozatlannak, ha egynél több.

Meghatározás. Lineáris egyenletrendszer esetén a mátrix

A = a rendszer mátrixának és a mátrixnak nevezzük

A*= a rendszer kiterjesztett mátrixának nevezzük

Meghatározás. Ha b 1 , b 2 , …,b m = 0, akkor a rendszert homogénnek mondjuk. Megjegyzés. Egy homogén rendszer mindig konzisztens, mert mindig van nulla megoldása.

Rendszerek elemi átalakításai.

1. Az egyik egyenlet mindkét részéhez hozzáadjuk a másik egyenlet megfelelő részeit, szorozva ugyanazzal a számmal, amely nem egyenlő nullával.

2. Egyenletek átrendezése helyeken.

3. Az egyenletrendszerből való eltávolítása, amely mindenki számára azonos x.

Cramer képletek.

Ez a módszer is csak olyan lineáris egyenletrendszerek esetében alkalmazható, ahol a változók száma egybeesik az egyenletek számával.

Tétel. N egyenletrendszer n ismeretlennel

ha a rendszer mátrixának determinánsa nem egyenlő nullával, akkor a rendszernek egyedi megoldása van, és ezt a megoldást a képletekkel találjuk meg: x i = Ahol D = det A, A D i a rendszer mátrixából az oszlop változtatásával kapott mátrix determinánsa én ingyenes tagok rovata b i.

D i =

Példa. Keressen megoldást az egyenletrendszerre:

D \u003d \u003d 5 (4 - 9) + (2 - 12) - (3 - 8) \u003d -25 - 10 + 5 = -30;

D 1 \u003d \u003d (28 - 48) - (42 - 32) \u003d -20 - 10 \u003d -30.

D 2 \u003d\u003d 5 (28-48) - (16-56) \u003d -100 + 40 = -60.

D 3 \u003d \u003d 5 (32-42) + (16-56) \u003d -50 - 40 \u003d -90.

Megjegyzés 1. Ha a rendszer homogén, pl. b i = 0, akkor D¹0 esetén a rendszer egyedi nulla megoldással rendelkezik x 1 \u003d x 2 \u003d ... \u003d x n \u003d 0.

2. megjegyzés. Nál nél D=0 A rendszernek végtelen számú megoldása van.

Inverz mátrix módszer.

Mátrix módszer olyan egyenletrendszerek megoldására alkalmazható, ahol az egyenletek száma egyenlő az ismeretlenek számával.

Legyen adott az egyenletrendszer: Készítsünk mátrixokat:

A= - változók együtthatói mátrixa vagy rendszermátrix;

B = - szabad tagok mátrixoszlopa;

X = - mátrix - ismeretlenek oszlopa.

Ekkor az egyenletrendszer felírható: A×X = B. Szorozd meg a bal oldalon az egyenlőség mindkét oldalán A -1: A -1 ×A × X = A -1 ×B óta A -1 × A \u003d E, Hogy E × X \u003d A -1 × B, akkor a következő képlet érvényes:

X \u003d A -1 × B

Így ennek a módszernek az alkalmazásához meg kell találni inverz mátrix.

Példa. Oldja meg az egyenletrendszert:

X = , B = , A =

Keresse meg az A -1 inverz mátrixot.

D = det A = 5(4-9) + 1(2 - 12) - 1(3 - 8) = -25 - 10 +5 = -30≠0 ⇒ létezik inverz mátrix.

M 11 = ; M21 = ; M 31 = ;

M 12 = M 22 = M 32 =

M 13 = M 23 = M 33 =

A -1 = ;

Ellenőrizzük:

A×A -1 =
=E.

Megtaláljuk az X mátrixot.

X \u003d \u003d A -1 B \u003d × = .

Rendszermegoldásokat kaptunk: x=1; y=2; z = 3.

4. Gauss-módszer.

Hagyja a rendszert m lineáris egyenletek -val n ismeretlen:

Feltéve, hogy a rendszerben az együttható a 11 különbözik a nullától (ha nem ez a helyzet, akkor az egyenlet nullától eltérő együtthatóval x 1). A rendszert a következőképpen alakítjuk át: az első egyenletet változatlanul hagyjuk, az ismeretlent pedig kizárjuk az összes többi egyenletből x Az 1. ábrán a fentiek szerint egyenértékű transzformációkat alkalmazunk.

Az így létrejövő rendszerben

,

feltételezve, hogy (ami mindig az egyenletek vagy az egyenleteken belüli tagok átrendezésével érhető el) a rendszer első két egyenletét változatlanul hagyjuk, a többi egyenletből pedig a második egyenlet felhasználásával, elemi transzformációk segítségével kizárjuk az ismeretlent. x 2. Az újonnan kapott rendszerben

feltételtől függően az első három egyenletet változatlanul hagyjuk, a többi közül pedig a harmadik egyenlet felhasználásával az elemi transzformációk kizárják az ismeretlent x 3 .

Ez a folyamat mindaddig folytatódik, amíg a három lehetséges eset egyike megvalósul:

1) ha ennek eredményeként olyan rendszerhez jutunk, amelynek az egyik egyenlete nulla együtthatóval rendelkezik minden ismeretlenre és egy nem nulla szabad tag, akkor az eredeti rendszer inkonzisztens;

2) ha a transzformációk eredményeként háromszög együtthatós mátrixú rendszert kapunk, akkor a rendszer kompatibilis és határozott;

3) ha fokozatos együtthatórendszert kapunk (és az (1) bekezdés feltétele nem teljesül), akkor a rendszer konzisztens és határozatlan.

Tekintsük a négyzetes rendszert : (1)

Ennek a rendszernek van együtthatója a A 11 különbözik a nullától. Ha ez a feltétel nem teljesül, akkor annak eléréséhez át kell rendezni az egyenleteket, előtérbe helyezve azt az egyenletet, amelyre az együttható x 1 nem egyenlő nullával.

Végezzük el a rendszer következő átalakításait:

1) mert a 11 ¹0, az első egyenletet változatlanul hagyjuk;

2) a második egyenlet helyett azt az egyenletet írjuk fel, amelyet úgy kapunk, hogy a második egyenletből kivonjuk az elsőt szorozva 4-gyel;

3) a harmadik egyenlet helyett a harmadik és az első különbségét írjuk 3-mal szorozva;

4) a negyedik egyenlet helyett a negyedik és az első közötti különbséget írjuk 5-tel szorozva.

Megkapta új rendszer egyenértékű az eredetivel, és az első kivételével minden egyenletben nulla együttható x 1 (ez volt az 1-4 transzformációk célja): (2)

A fenti transzformációhoz és minden további átalakításhoz nem szabad teljesen átírni a teljes rendszert, ahogy az imént történt. A kezdeti rendszer mátrixként ábrázolható

. (3)

A (3) mátrixot hívjuk kiterjesztett mátrix az eredeti egyenletrendszerhez. Ha eltávolítjuk a szabad tagok oszlopát a kiterjesztett mátrixból, akkor azt kapjuk rendszer együttható mátrix, amit néha egyszerűen neveznek rendszermátrix.

A (2) rendszer a kiterjesztett mátrixnak felel meg

.

Alakítsuk át ezt a mátrixot a következőképpen:

1) az első két sort változatlanul hagyjuk, mivel az elem a 22 nem nulla;

2) a harmadik sor helyett a második sor és a duplázott harmadik sor különbségét írjuk;

3) a negyedik sor helyébe a második sor duplázott és a negyedik sor 5-tel szorzott különbsége lép.

Az eredmény egy ismeretlen rendszernek megfelelő mátrix x Az 1 minden egyenletből ki van zárva, kivéve az elsőt és az ismeretlent x 2 - az első és a második kivételével minden egyenletből:

.

Most megszüntetjük az ismeretlent x 3 a negyedik egyenletből. Ehhez az utolsó mátrixot a következőképpen alakítjuk át:

1) az első három sor változatlan marad, mivel a 33 ¹ 0;

2) a negyedik sor helyébe a harmadik, 39-gyel megszorzott különbség és a negyedik sor kerül: .

A kapott mátrix megfelel a rendszernek

. (4)

Ennek a rendszernek az utolsó egyenletéből kapjuk x 4 = 2. Ezt az értéket behelyettesítve a harmadik egyenletbe, azt kapjuk x 3 = 3. Most a második egyenletből következik, hogy x 2 = 1, és az elsőtől - x 1 = -1. Nyilvánvaló, hogy a kapott megoldás egyedi (mivel az érték x 4, akkor x 3 stb.).

Meghatározás: Nevezzünk meg egy négyzetmátrixot, amelynek főátlóján nullától eltérő számok, a főátló alatt pedig nullák találhatók, háromszög mátrix.

A (4) rendszer együtthatómátrixa egy háromszögmátrix.

Megjegyzés: Ha elemi transzformációk segítségével egy négyzetrendszer együtthatói mátrixa háromszögmátrixra redukálható, akkor a rendszer konzisztens és határozott.

Vegyünk egy másik példát: . (5)

Végezzük el a rendszer kiterjesztett mátrixának alábbi transzformációit:

1) hagyja változatlanul az első sort;

2) a második sor helyett a második és az első sor közötti különbséget írjuk;

3) a harmadik sor helyett a harmadik sor közötti különbséget írjuk, és az elsőt háromszorozzuk;

4) a negyedik sor helyébe a negyedik és az első közötti különbség lép;

5) az ötödik sor helyébe az ötödik sor és az első sor kétszerese közötti különbség lép.

A transzformációk eredményeként megkapjuk a mátrixot

.

Ennek a mátrixnak az első két sorát változatlanul hagyva elemi transzformációkkal a következő alakra redukáljuk:

.

Ha most a Gauss-módszert követve, amelyet az ismeretlenek egymás utáni kiküszöbölésének módszerének is neveznek, a harmadik sor használatával az együtthatókat nulláról nullára hozzuk x 3 a negyedik és ötödik sorban, majd miután a második sor összes elemét elosztjuk 5-tel és a harmadik sor összes elemét elosztjuk 2-vel, megkapjuk a mátrixot

.

A mátrix utolsó két sora a 0 egyenletnek felel meg x 1 +0x 2 +0x 3 +0x 4 +0x 5 = 0. Ez az egyenlet bármely számhalmazra teljesül x 1 ,x 2, ¼, x 5, és el kell távolítani a rendszerből. Így az imént kapott kiterjesztett mátrixú rendszer ekvivalens az űrlap kiterjesztett mátrixú rendszerével.

. (6)

Ennek a mátrixnak az utolsó sora felel meg az egyenletnek
x 3 – 2x 4 + 3x 5 = -4. Ha ismeretlen x 4 és x 5 tetszőleges értékeket ad meg: x 4 = 1-től; x 5 = 2-től, akkor a (6) mátrixnak megfelelő rendszer utolsó egyenletéből kapjuk x 3 = –4 + 21-től – 32-től. Kifejezések helyettesítése x 3 ,x 4 és x 5-öt ugyanannak a rendszernek a második egyenletébe kapjuk x 2 = –3 + 21-től – 22-től. Most az első egyenletből megkaphatjuk x 1 = 4 – 1-től+ 2-től. A rendszer végső megoldását a forma ábrázolja .

Tekintsünk egy téglalap alakú mátrixot A, amely az oszlopok számát tartalmazza m nagyobb, mint a sorok száma n. Egy ilyen mátrix A hívjuk lépett.

Nyilvánvaló, hogy a (6) mátrix egy lépcsős mátrix.

Ha egy egyenletrendszerre ekvivalens transzformációk alkalmazásakor legalább egy egyenletet a következőre redukálunk

0x 1 + 0x 2 + ¼0 x n = b j (b j ¹ 0),

akkor a rendszer inkonzisztens vagy inkonzisztens, mivel nincs számkészlet x 1 , x 2, ¼, x n nem teljesíti ezt az egyenletet.

Ha a rendszer kiterjesztett mátrixának átalakításakor az együtthatók mátrixa lépésformára redukálódik, és a rendszer nem bizonyul inkonzisztensnek, akkor a rendszer konzisztens és határozatlan, azaz végtelenül sok megoldás.

Ez utóbbi rendszerben az összes megoldást úgy kaphatjuk meg, hogy a paraméterekhez konkrét számértékeket adunk 1-tőlÉs 2-től.

Meghatározás: Azokat a változókat, amelyek együtthatói a lépésmátrix főátlóján vannak (ez azt jelenti, hogy ezek az együtthatók nem nullák), o fő-. A fenti példában ezek az ismeretlenek x 1 , x 2 , x 3. A többi változót hívjuk kiskorú. A fenti példában ezek a változók x 4 és x 5. A nem elsődleges változókhoz tetszőleges értéket rendelhetünk, vagy paraméterekkel fejezhetjük ki, amint az az utolsó példában is történt.

Az alapvető változókat egyedileg fejezzük ki a nem alapvető változókkal.

Meghatározás: Ha a nem alapváltozóknak meghatározott számértékeket adunk, és a fő változókat ezeken keresztül fejezzük ki, akkor a kapott megoldást ún. magándöntés.

Meghatározás: Ha a nem alapváltozókat paraméterekkel fejezzük ki, akkor megoldást kapunk, amelyet ún általános megoldás.

Meghatározás: Ha minden nem elsődleges változó nulla értéket kap, akkor a kapott megoldást hívjuk alapvető.

Megjegyzés: Ugyanaz a rendszer néha az alapvető változók különböző halmazaira redukálható. Így például felcserélheti a 3. és 4. oszlopot a mátrixban (6). Akkor a fő változók lesznek x 1 , x 2 ,x 4 és kisebb - x 3 és x 5 .

Meghatározás: Ha két különböző alapváltozó-halmazt kapunk, különböző módon keresve ugyanazt a rendszert, akkor ezek a halmazok szükségszerűen ugyanannyi változót tartalmaznak, ún. rendszer rangja.

Vegyünk egy másik rendszert, amelynek végtelenül sok megoldása van: .

Végezzük el a rendszer kiterjesztett mátrixának transzformációját Gauss módszerrel:

.

Mint látható, lépésmátrixot nem kaptunk, de az utolsó mátrixot a harmadik és negyedik oszlop felcserélésével lehet átalakítani: .

Ez a mátrix már lépésenkénti. A hozzá tartozó rendszernek két kisebb változója van - x 3 , x 5 és három fő - x 1 , x 2 , x 4. Az eredeti rendszer megoldását a következő formában mutatjuk be:

Íme egy példa egy olyan rendszerre, amelynek nincs megoldása:

.

A rendszer mátrixát a Gauss-módszer szerint alakítjuk át:

.

Az utolsó mátrix utolsó sora a feloldhatatlan egyenletnek felel meg 0x1 + 0x2 + 0x3 = 1. Ezért az eredeti rendszer következetlen.

3. számú előadás.

Téma: Vektorok. Skalár, vektor és vektorok vegyes szorzata

1. A vektor fogalma. Vektorok kollinaritása, ortogonalitása és koplanaritása.

2. Lineáris művelet vektorokon.

3. Vektorok pontszorzata és alkalmazása

4. vektor termék vektorok és alkalmazása

5. vegyes termék vektorok és alkalmazása

1. A vektor fogalma A vektorok kollinaritása, ortogonalitása és komplaritása.

Meghatározás: A vektor egy szakasz, amelynek kezdőpontja A és végpontja B.

Kijelölés: , ,

Meghatározás: Egy vektor vektorának hossza vagy modulusa egy szám, hosszával egyenlő vektort reprezentáló AB szegmens.

Meghatározás: Egy vektort nullának nevezünk, ha a vektor eleje és vége megegyezik.

Meghatározás: Az egységnyi hosszúságú vektort egységvektornak nevezzük. Meghatározás: A vektorokat kollineárisnak nevezzük, ha ugyanazon az egyenesen vagy párhuzamos egyeneseken helyezkednek el. ( || ).

Megjegyzés:

1. A kollineáris vektorok egyformán vagy ellentétes irányban irányíthatók.

2. A nulla vektort bármely vektorhoz képest kollineárisnak tekintjük.

Meghatározás: Két vektort egyenlőnek mondunk, ha kollineárisak,

azonos irányúak és azonos hosszúságúak ( = )